质因数（数论）：寻找质因数，一题多写_如何找出一个数的质因数-CSDN博客

本文链接：https://blog.csdn.net/djsbdbk/article/details/146276760

基本概念

质数（素数）：大于 1 的自然数，且只能被 1 和它本身整除的数。例如：2, 3, 5, 7, 11, …
质因数：一个数的质因数是能整除它的质数。（既是因数又是质数）例如，12 的质因数是 2 和 3。
质因数分解：将一个数表示为质数的乘积。

思路：

已经学会质数的筛法，忘记请看：欧拉筛（线性筛）：找出所有小于等于给定整数n的质数的算法-CSDN博客

我们将这个数组乘积后的数的所用质数进行筛选质数的预处理，然后将原数组中的每一个元素依次对质数表中的数进行取余，如果取余结果为零，那么这个质数就是质因数之一。

为什么要求nums数组乘积的质因数，却用每个数组中的元素来确定质因数呢？原因是：数组中的每一个元素都是A的因数，而如果找A的质因数用数组中的元素进行判断质因数即可；

class Solution {
    public int distinctPrimeFactors(int[] nums) {
        int n=(int)1e3;//要用(int)转换一下，否则不行
        boolean[]bo=new boolean[n+1];//因为有零所以多一个
        List<Integer> isprime=new ArrayList<>();
        Arrays.fill(bo,true);//快速赋值为true
        for(int i=2;i<=n;i++){
            if(bo[i]==true){
                isprime.add(i);
            }
            for(int j=0;j<isprime.size();j++){
                int p=isprime.get(j);
                int m=i*p;
                if(m>n){
                    break;
                }
                bo[m]=false;
                if(i%p==0){
                    break;
                }
            }
        }
        Set<Integer> ans=new HashSet<>();//要找到质因数的个数，不能有重复的元素，set集合有不重复性
        for(int i=0;i<nums.length;i++){
            for(int j=0;j<isprime.size();j++){
                if(isprime.get(j)>nums[i]){//大于了就没必要判断了，连因数都不是
                    break;
                }
                if(nums[i]%isprime.get(j)==0){//能被整除，所以是因数，又因为是质数，所以为质因数
                    ans.add(isprime.get(j));//添加到set集合中
                }
            }
        }return ans.size();//set集合的长度就是质因数的个数;
    }
}

HashSet相关知识请看：一题多写（1），打牢基础（哈希set相关用法）-CSDN博客

优化：

在写双层for循环时，当使用的元素不在是单纯的一个索引时，而是集合，数组....里的元素时，要写的代码会比较长。当我们在思考时，思路是正确的，而可能会不注意，将要使用数组或集合中的元素写成索引 i 或 j 等其他错误，并且不容易看出,这时使用强制for循环就可以将代码更加清晰，即使出错也更好看出。

for(int a:nums){
            for(int is:isprime){
                if(is>a){
                    break;
                }
                if(a%is==0){
                    ans.add(is);
                }
            }
        }

将上面的双层for循环改为强制for循环后更加简洁；

取巧写法(能成就是好写法)：

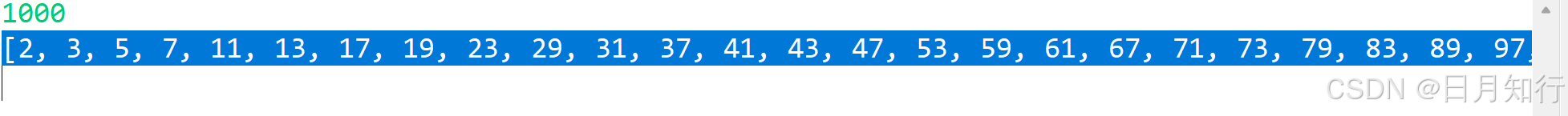
可以将用欧拉筛，将要用的数组存到一个数组中，直接使用此质数数组，可以让代码用时更短；

class Solution {
    public int distinctPrimeFactors(int[] nums) {
        int[]isprime={2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997};
        Set<Integer> ans=new HashSet<>();
        for(int a:nums){
            for(int is:isprime){
                if(is>a){
                    break;
                }
                if(a%is==0){
                    ans.add(is);
                }
            }
        }
        return ans.size();
    }
}

暴力思路：

试除法

举例：

（知道质数有2，3，5，7......）相求30的所用质因数，用30先除以2，等于15，在用15除以2，发现不能整除，再用15 除以3，等于5，而5又是质数，且不能再除以一个数得到一个整数，因此30的质因数有2，3，5。这是求解一个数的质因数的试除法思路。试除法其实不需要知道有哪些质数，按照试除方式从小到大试除就能解决。

用代码模拟上述思路：外层for循环：求题目中所有nums数组中所有的数进行乘积，求乘积后的质因数，可以等同与求数组中各个元素的质因数。

内层for循环：终止条件i*i<=x,

思路其实就是埃氏筛求合数的逆过程：埃氏筛（Java）：找出所有小于等于给定整数n的质数的算法-CSDN博客

将数组中的一个元素对2进行整除，如果能被整除，那么2是质因数，将2添加到set集合中，将nums[的一个元素]x,一直除以2，对x进行保存，直到不能整除为止，此时内层for循环结束一次，i++，进行第二次，再用保存的x对3进行试除，如果能整除，将3保存到set集合中，再用x一直除以3，对x进行保存，直到不能再整除3，此时内层for循环又结束一次，i++，进行第三次，x对4进行试除，因为前面已经对2进行试除，所以对4的结果也已处理过了且也就是说此时的x不可能还能除尽4，4不会被录入进set集合...接着看5...再看6，6可以看成2和3 相乘，所以也被处理过，此时的x不可能还能除尽6，6不会被放进set集合......最后除后剩余的数如果大于1，那么这个数是“饱经风霜”的，将所有的<根号x的数试除了一边，这个数一定是质数，不能再进行分解，又应为是除剩下的，也是质因数。

试除法的循环条件是 i * i <= x（即 i ≤ √x）。当循环结束时，所有小于等于 √x 的整数 i 都已尝试过。此时：

若剩余 x > 1，说明它没有小于等于其平方根的因数。
根据数学性质，任何合数至少有一个质因数小于等于它的平方根。

质数是分解的终点（不能再分解），合数可以分解且可以分解为质数

最后set集合的去重性，所有质因数已被保存，且不会重复。

class Solution {
    public int distinctPrimeFactors(int[] nums) {
        Set<Integer> set = new HashSet<>();
        for (int x : nums) {
            for (int i = 2; i * i <= x; i++){
                if (x % i == 0) {
                    set.add(i);
                    while (x % i == 0){
                        x /= i;
                    }
                }
            }                
            if (x > 1)set.add(x);
        }
        return set.size();
    }
}