本文试图通过几幅简明的图来介绍遗传算法。
背景
当一些问题不存在确定性的最优解法,或者说最优解法的施展时间长的1-B,那我们就得开始考虑点其他路子了。
比如说旅行商问题:
旅行商要去很多城市卖货,为了节省时间,它一个城市只去一次,最后还得返回原城市,因为他老婆不允许他离开太久。
它怎么走比较合算?
城市的分布可能会像下面这样:

旅行商会想就是把所有城市路线做个排列(一半),然后看看哪条路线最短就按哪条路线来。
好吧,如果旅行商要去的城市只有3-5个还好说,如果旅行商生意太好,可能要去几十个城市,那这个方法行不通。
为什么呢?
O(1)<O(logN)<O(N)<O(N2)<O(N!)
如果你熟悉时间复杂度,一定明白我在说什么,不信,自己试试34的阶乘算出来是个什么,亲,如果钱包有那么多钱那该多好。
好在,达尔文总结出了自然界的一个不知确否的道理,就是生物通过优胜劣汰的自然选择过程,来完成进化。
这个过程,看起来像是一堆随机不确定的微小变化中,让确定而显著的优势变化延续下来。
谁强,谁就更有话语权,资源就该属于这种强强的亲,而弱弱的主因为无法抗拒灾难和考验,最终就被淹没在进化的过程中。
遗传算法
既然生命都可以进化,现存的生物都是摸爬滚打、出生入死过来的,那么解决点计算问题还有什么复杂的。
于是,我们想着用可以量化的数学的方式去表达这种进化过程,然后让计算机来模拟自然选择和种群的演化,看看会有什么样的优质个体(解)出现。
也许不能得到一个最优的解,但旅行商恐怕不得不接受一个差不多的解:
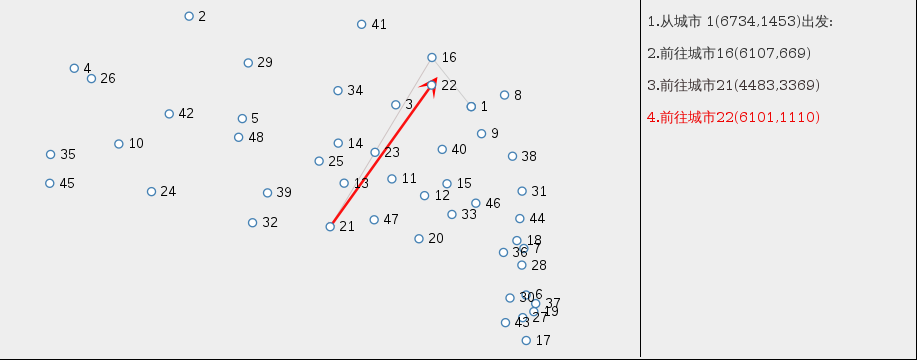
好吧,那我们来认识一下所谓的遗传算法(genetic algorithms)。
遗传算法,是一种进化算法,进化大家都明白。
那么生命的变化在于基因的变化,什么是基因呢,我们不关注真正的生物基因,毕竟这里不是讨论生殖问题:
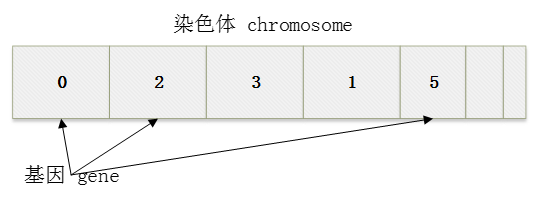
如果把基因(gene)当做一个经过编码的元素,用一个数组或者列表来存储一组基因,这组基因就是染色体(chromosome)。
<code class="language-java hljs has-numbering" style="display: block; padding: 0px; background-color: transparent; color: inherit; box-sizing: border-box; font-family: 'Source Code Pro', monospace;font-size:undefined; white-space: pre; border-top-left-radius: 0px; border-top-right-radius: 0px; border-bottom-right-radius: 0px; border-bottom-left-radius: 0px; word-wrap: normal; background-position: initial initial; background-repeat: initial initial;"> <span class="hljs-javadoc" style="color: rgb(136, 0, 0); box-sizing: border-box;">/**
* 基因
*/</span>
<span class="hljs-keyword" style="color: rgb(0, 0, 136); box-sizing: border-box;">private</span> <span class="hljs-class" style="box-sizing: border-box;"><span class="hljs-keyword" style="color: rgb(0, 0, 136); box-sizing: border-box;">class</span> <span class="hljs-title" style="box-sizing: border-box; color: rgb(102, 0, 102);">Gene</span> {</span>
<span class="hljs-javadoc" style="color: rgb(136, 0, 0); box-sizing: border-box;">/**
* 编码
*/</span>
<span class="hljs-keyword" style="color: rgb(0, 0, 136); box-sizing: border-box;">int</span> value;
<span class="hljs-javadoc" style="color: rgb(136, 0, 0); box-sizing: border-box;">/**
* 等位基因(编码的值)
*/</span>
Integer Allele;
}
<span class="hljs-keyword" style="color: rgb(0, 0, 136); box-sizing: border-box;">public</span> <span class="hljs-class" style="box-sizing: border-box;"><span class="hljs-keyword" style="color: rgb(0, 0, 136); box-sizing: border-box;">interface</span> <span class="hljs-title" style="box-sizing: border-box; color: rgb(102, 0, 102);">IChromosome</span> {</span>
<span class="hljs-keyword" style="color: rgb(0, 0, 136); box-sizing: border-box;">public</span> Genes[];
}</code><ul class="pre-numbering" style="box-sizing: border-box; position: absolute; width: 50px; background-color: rgb(238, 238, 238); top: 0px; left: 0px; margin: 0px; padding: 6px 0px 40px; border-right-width: 1px; border-right-style: solid; border-right-color: rgb(221, 221, 221); list-style: none; text-align: right;"><li style="box-sizing: border-box; padding: 0px 5px;">1</li><li style="box-sizing: border-box; padding: 0px 5px;">2</li><li style="box-sizing: border-box; padding: 0px 5px;">3</li><li style="box-sizing: border-box; padding: 0px 5px;">4</li><li style="box-sizing: border-box; padding: 0px 5px;">5</li><li style="box-sizing: border-box; padding: 0px 5px;">6</li><li style="box-sizing: border-box; padding: 0px 5px;">7</li><li style="box-sizing: border-box; padding: 0px 5px;">8</li><li style="box-sizing: border-box; padding: 0px 5px;">9</li><li style="box-sizing: border-box; padding: 0px 5px;">10</li><li style="box-sizing: border-box; padding: 0px 5px;">11</li><li style="box-sizing: border-box; padding: 0px 5px;">12</li><li style="box-sizing: border-box; padding: 0px 5px;">13</li><li style="box-sizing: border-box; padding: 0px 5px;">14</li><li style="box-sizing: border-box; padding: 0px 5px;">15</li><li style="box-sizing: border-box; padding: 0px 5px;">16</li><li style="box-sizing: border-box; padding: 0px 5px;">17</li></ul>
好,有了这个表达基础,就可以很好的描述进化过程了。
为了简化问题,突出本质,我们简化种群(population)的描述:
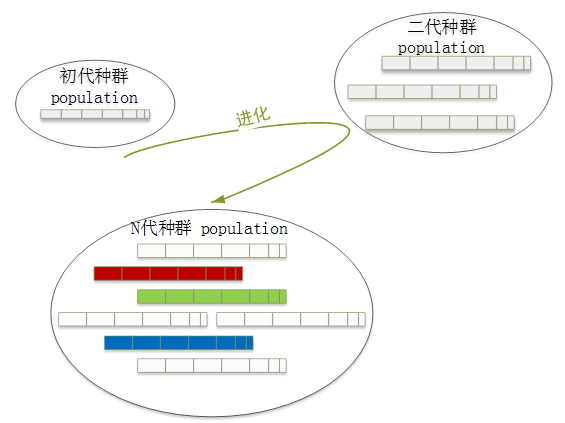
这张图告诉我们
种群包含了若干个个体(染色体),一次又一次的进化,让种群规模变大,个体数目变多,优质个体也越来越多。
那么我们的解可能就蕴藏其中呢?
这幅图没有告诉我们关于进化的细节信息,显然,我们需要了解进化到底是什么东东。

你可能觉得我骗了你,但事实上,进化只有三维,就是选择(select)、交叉(crossover)和变异(mutate)。
让我们继续认识进化。
选择
选择就是选择,为什么选择,因为要优胜劣汰:
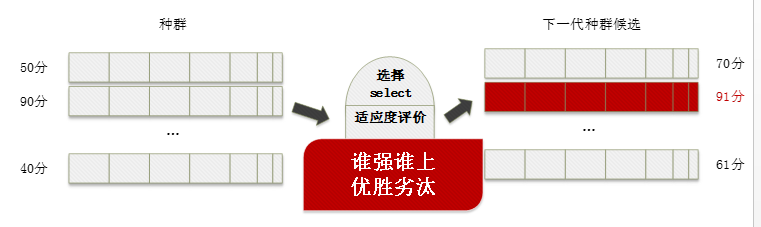
个体们在种群内部,不能闲着,都得上学打工养老婆,所以它们需要通过各种考试和考核。
通过考核的加薪升职,否则就扫地出门。
上面的图可以告诉我们,选择是针对种群的操作,选择的目的是为了确保下一代种群的质量更佳。
交叉
那么,个体之间又如何出现了差异?这要从个体的爸爸妈妈说起,现在不是都搞什么优质基因人工D孕吗,好吧,个体的差异就是因为繁殖而出现的。
人家都会说,哇,这孩子长得跟花儿似的!
其实,可能是这孩子他妈妈很漂亮,优秀的基因得以传递。
也有人会说,哦哟,这孩子眼睛跟他爹一样乌黑乌黑的,说明他爹可能是个码农,而且孩子不幸遗传了他爹的这些个…
下面将进入少儿不宜环节:
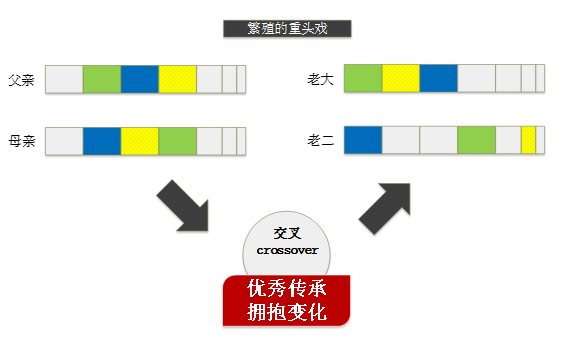
至于激情的细节如何,本篇不打算讨论交叉的具体算法,但要说明它的意思:
交叉就是对两组父个体进行基因交叉,从而形成1个或者1组新的基因序列或染色体。
交叉可以随机,但尽量要避免无意义的交叉。
交叉的目的是在个体中增加大幅度的变化,并集成父母的优质基因。
交叉是遗传算法最重要的一步操作。
变异
也许孩子是个富二代,也许孩子是个官二代,但有可能就是一个普通的孩子,令人遗憾的是,他比较喜欢他爸,他幼稚的心灵觉得他爸挺牛X的,所以他觉得码农挺牛X的。
不同的,这孩子喜欢汇编,囧~
这是他的个性,谁也阻止不了,人家会说,这孩子一点都不像他妈妈。
那么这种个性,虽然不全是,但基因方面的原因可能是:
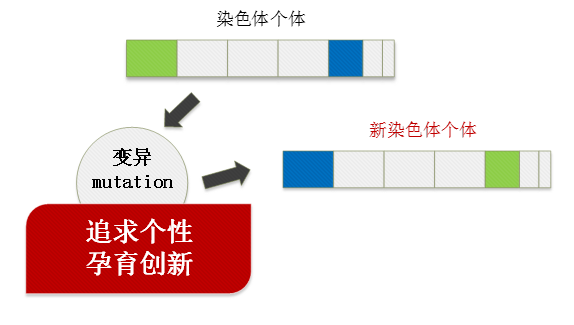
变异其实没有交叉重要,而且可能产生极坏的变异。
但变异是一种对交叉的补充和完善,也是一种有风险的创新。
旅行商
现在我们回到旅行商问题,如果对城市进行编号,比如
1、2、3、...、N
,那么一条路线就是这样:
3,10,2,1,...,20,3
每个城市的编号就是一个基因,城市的排列就是一个染色体(基因序列)。
那么,在经过若干次进化之后,优质染色体就可以被挑选出来,旅行商也就得到了一个接近最短的旅行路线:
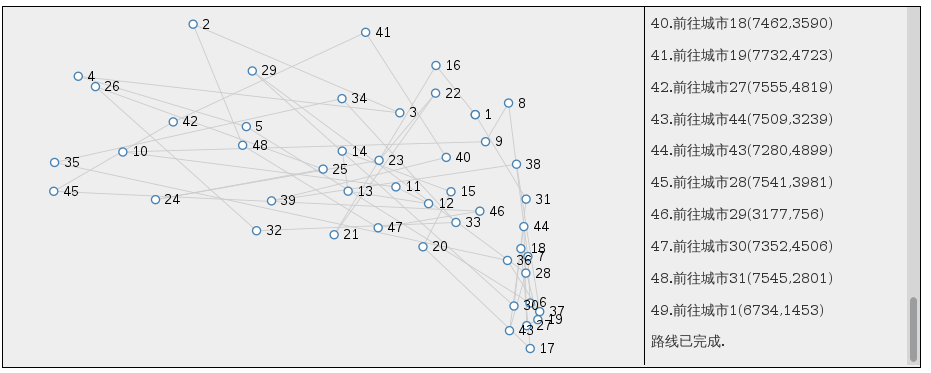
亲,这就是遗传算法。































 125
125

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








