浇水问题c程序

浇 水问题

问题描述

瓜农王大爷去年种西瓜赚了不少钱。看到收入不错，今年他又重新开辟了n个西瓜地。
为了能给他的n个西瓜地顺利的浇上水，对于每个西瓜地他可以选择在本地打井，也可以修管道从另一个瓜地（这个瓜地可能打了井；也可能没打井，他的水也是从其他瓜地引来的）将水引过来。
当然打井和修管道的费用有差别。已知在第i个西瓜地打井需要耗费wi元，在第i、j个西瓜地之间修管道需要耗费pi,j元。
现在的问题是：王大爷要想使所有瓜地都被浇上水，至少需要花费多少钱（打井与修管道的费用和）？
由于瓜地较多，王大爷无法选择在哪些（个）瓜地打井，哪些西瓜地之间修管道。
请你编程帮王大爷做出决策，求出最小费用。

输入格式

第1行，一个正整数n，代表西瓜地的数量。
以下n行，依次给出整数w1..wn（每块西瓜地的打井费用）。
紧接着是一个n*n的整数矩阵，矩阵的第i行第j列的数代表pi,j（两块西瓜地之间建立管道的费用）。每行的两个数之间有一个空格隔开。

6
5
4
4
3
1
20
0 2 2 2 9 9
2 0 3 3 9 9
2 3 0 4 9 9
2 3 4 0 9 9
9 9 9 9 0 9
9 9 9 9 9 0

样例说明

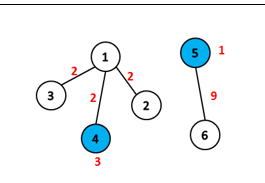
在第4个瓜地打井（费用为3），然后将第2,3，4个瓜地与第1个瓜地间修管道（费用分别是2,2,2），这样水可以经过管道从4流向1，然后经1再流向2和3；
在第5个瓜地打井（费用为1），5和6之间修管道（费用为9）。
这样一共打了2口井，修了4条管道，能给所有的6个瓜地浇水，费用是：3+2+2+2+1+9=19。

数据规模和约定

对于所有数据，1<=N<=300，1<=wi<=100000；pi,i=0，1<=pi,j=pj,i<=100000。

算法思路

应用贪婪算法，先在打井费用最便宜的地打井，用已有水源的地更新没有水源的地（判断两者之间是否适合挖管道），若所有地都有水源，算法结束，否则，打下一口井

源程序

 #include <stdio.h>
 int flg[1000];                  /*保存打井或者挖管道信息，0挖管道，1打井 */
int barr[1000][1000];
int arr[1000];
void update(int *st, int n);
int
find(int *arr, int n, int last)/*找出打井费用最低的地*/
{
    int i;
    int min = arr[1];
    int rt = 1;
    for (i = 2; i < n + 1; i++)
            if (arr[i] < min && arr[i] > last) {
                    min = arr[i];
                    rt = i;
            }
    return rt;
}
int
check(int *a, int n)/*检查当前所有土地是否都有水源*/
{
    int i;
    for (i = 1; i < n + 1; i++) {
            if (a[i] > 0) ;
            else
                    break;
    }
    if (i == n + 1)
            return 0;
    else
            return 1;
}
int
main(void)
{
    int i, j, k;
    int n;
    if (freopen("water.in", "r", stdin) == NULL)
            return -1;
    scanf("%d", &n);
    int st[n + 1];          /*保存有水源的地打井或者挖管道的费用 */
    for (i = 1; i < n + 1; i++)
            scanf("%d", &arr[i]);

    for (i = 1; i < n + 1; i++)
            for (j = 1; j < n + 1; j++)
                    scanf("%d", &barr[i][j]);

    for (i = 0; i < n + 1; i++) {
            st[i] = 0;
            flg[i] = 0;
    }
    k = find(arr, n, 0);

    while (check(st, n) != 0) {
            if (st[k] == 0) {
                    st[k] = arr[k];
                    flg[k] = 1;
                    printf("第%d块地打井 \n", k);
            }
            for (i = 1; i < n + 1; i++) {
                    if (st[i] > 0)
                            continue;
                    int flag = 1;
                    if (i == k || barr[i][k] > arr[i])
                            continue;
                    else {
                            for (j = 1; j < n + 1; j++) {
                                    if (i != j && barr[i][j] < barr[i][k]
                                        && j != k) {
                                            flag = 0;
                                            break;
                                    }
                            }
                            if (flag == 1 && st[i] == 0) {
                                    st[i] = barr[i][k];
                                    printf
                                        ("第%d块地与第%d块地挖管道\n",
                                         i, k);
                            }
                    }
            }
            update(st, n);
            k = find(arr, n, st[k]);
    }

    for (i = 1; i < n + 1; i++)
            printf("%d ", st[i]);
    printf("\n");
    return 0;
}
/*当i块地接通水源以后别的地可以通过与挖它管道接通水源
 * 本函数作用是确定没有水源的地与i块地之间的管道*/
void
update(int *st, int n)
{
    int i, j, k, l;
    for (l = 1; l < n + 1; l++) {
            if (st[l] > 0 && flg[l] == 0)
                    k = l;
            else
                    continue;

            for (i = 1; i < n + 1; i++) {
                    if (st[i] > 0 && flg[i] == 1)
                            /*flg[i]=1，打井的地，费用信息不能更新 */
                            continue;
                    int flag = 1;
                    /*跳过与第i块间管道费用比打井贵的地 */
                    if (i == k || barr[i][k] > arr[i])
                            continue;
                    else {
                             /**/ for (j = 1; j < n + 1; j++) {
                                    if (i != j && barr[i][j] < barr[i][k]
                                        && j != k) {
                                            flag = 0;
                                            break;
                                    }
                            }
                            if (flag == 1 && st[i] == 0 && flg[i] == 0) {
                                    st[i] = barr[i][k];
                                    printf
                                        ("第%d块地与第%d块地挖管道\n",
                                         i, k);

                            }
                    }
            }
    }
}

请多多指教！