堆和堆排序

堆，是一棵完全二叉树，根的值大于左右子树中所有结点的值，左右子树也是堆，除此之外，对其它元素之间的大小关系（如左右子树之间元素大小关系）没有要求。这是大根堆，如果把“大于”换成“小于”，就是小根堆，这里都以大根堆为例。

由于堆是完全二叉树，所以可以用数组来模拟，在数据结构上算是比较简单。用数组模拟二叉树（当然也包括堆）的话，如果根节点的下标为0的话，则对于每个结点i，其左孩子下标为2*i+1；其右孩子下标为2*i+2。

 

堆有一个重要的应用是堆排序

堆排序的思想很简单，仍然以大根堆为例。在数组的非降序排序中，需要使用的就是大根堆，因为根据大根堆的性质可知，最大的值一定在堆顶。每次把堆顶最大的元素拿出来，组成有序序列，剩下的再组织成大根堆。

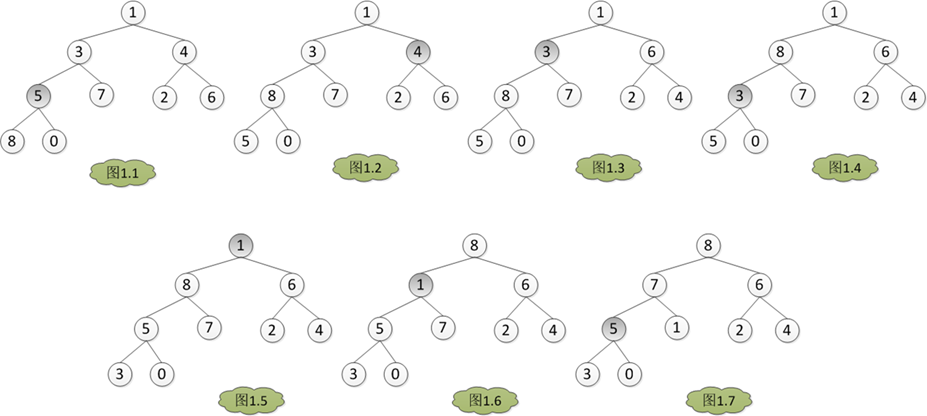
首先要建立一个堆，而建堆的核心内容是调整堆，使二叉树满足堆的定义（每个节点的值都不大于其父节点的值）。调堆的过程应该从最后一个非叶子节点开始，假设有数组A = {1, 3, 4, 5, 7, 2, 6, 8, 0}。那么调堆的过程如下图，数组下标从0开始，A[3] = 5开始。分别与左孩子和右孩子比较大小，如果A[3]最大，则不用调整，否则和孩子中的值最大的一个交换位置，在图1中是A[7] > A[3] > A[8]，所以A[3]与A[7]对换，从图1.1转到图1.2。建堆完成之后，堆如图1.7是个大根堆。

其次，排序过程

将待排序区分为无序区和有序区，无序区在前，有序区在后。未排序前无序区为整个待排序区间，没有有序区。排序的过程是，不断地将无序区构造成一个大根堆，这样无序区中的最大元素便被放置在了数组的最前面即根的位置，然后将无序区的第一个元素与最后一个元素交换，此动作将无序区的长度缩小一，将有序区的长度扩大一，即有序区前进一，无序区向前退一。然后将新的无序区（由于根节点的变化，此时很可能已经不是大根堆）重新调整为大根堆，等待下一次的交换。如此往复，不断地将无序区的最大元素添加到有序区的前面，同时缩小无序区，直到有序区占满待排序区为止。由于进行元素交换前，无序区是一个大根堆，即左子树和右子树都是大根堆，所以根节点变化后左右子树仍然都是大根堆，无序区里的最大元素一定在新根节点、左右子树的根节点这三个结点里。先存储新的根节点的值以待后用。如果新的根结点最大，说明已经是大根堆，调整完毕；否则比较左右子树根节点，找出较大的，它是无序区现存的最大元素，应该作为新的大根堆中的根，所以将此节点上调至根节点位置，接下来就只需要调整此结点原来所在的子树为大根堆即可（因为大根堆对左右子树之间元素的大小关系没有要求！）。这是一个迭代的过程，当某一个需要调整的子树调整前就已经是大根堆（待调整的根节点比左右子树根节点都大）时，或者下标已经超出无序区范围时，迭代过程结束，无序区已经调整为大根堆。这就是调整一个左右子树都为大根堆的完全二叉树为大根堆的过程。

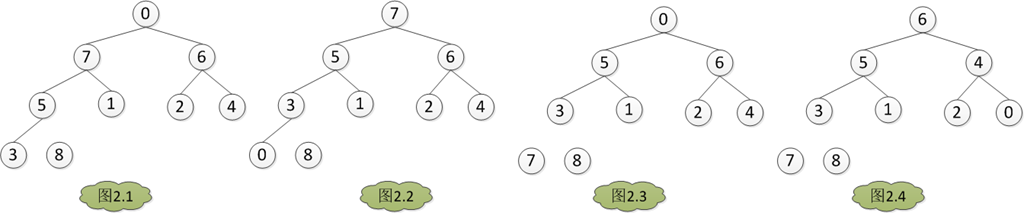
如图将A[0] = 8 与 A[heapLen-1]交换,然后heapLen减一，如图2.1，然后调整除最后一个元素的数组为大根堆，如图2.2。如此交换堆的第一个元素和堆的最后一个元素，然后堆的大小heapLen减一，对堆的大小为heapLen的堆进行调堆，如此循环，直到heapLen == 1时停止，最后得一个排序的序列。

 

下面给出代码，根据调整时被调整结点的行为，将调整函数称为SiftUp,并且给出了SiftUp递归和非递归两种算法。

#include <iostream>
using namespace std;

//使得以i为根的子堆符合堆得性质
//i is the root of the heap, and its children is less than arr[i]
void SiftUp_digui(int* arr, int i, int size)//递归算法
{
	if(i >= size)
		return;
	int lt = 2*i + 1, rt = 2*i + 2;
	int largest = i;

	if(lt <= size && arr[largest] < arr[lt])
		largest = lt;
	if(rt <= size && arr[largest] < arr[rt])
		largest = rt;

	if(largest != i)
	{
		int tmp = arr[i];
		arr[i] = arr[largest];
		arr[largest] = tmp;
		SiftUp_digui(arr, largest, size);
	}
	return;
}

//使得以i为根的子堆符合堆得性质
void SiftUp(int* arr, int i, int size)//非递归算法
{
	int parent = i;
	int lchild = 2*i + 1, rchild = 2*i + 2;
	while( lchild <= size | rchild <= size)
	{
		int largest = parent;
		if(lchild <= size && arr[largest] < arr[lchild])
			largest = lchild;
		if(rchild <= size && arr[largest] < arr[rchild])
			largest = rchild;
		if(largest == parent)
			break;
		else
		{
			int tmp = arr[parent];
			arr[parent] = arr[largest];
			arr[largest] = tmp;
			parent = largest;
			lchild = largest * 2 + 1;
			rchild = largest * 2 + 2;
		}
	}
}


//build arr to a heap, arr[0..size],
//arr[size] is the last element of the arrry
void BuildHeap(int* arr, int lastleaf)
{
	int lastparent = (lastleaf-1)/2;
	//i is parent, and its children are 2*i+1 and 2*i+2

	for( int i = lastparent; i >= 0; --i)
		//SiftUp_digui(arr, i, lastleaf);
		SiftUp(arr, i, lastleaf);
}

void HeapSort(int* arr, int arrlength)
{
	int lastleaf = arrlength -1;
	BuildHeap(arr, lastleaf);

	for(int i = lastleaf; i > 0;)
	{
		int tmp = arr[0];
		arr[0] = arr[i];
		arr[i] = tmp;
		//SiftUp_digui(arr, 0, --i);
		SiftUp(arr,0,--i);
	}
}

int main(int argc, char* argv[])
{
	int x6[9] = {1, 3, 4, 5, 7, 2, 6, 8, 0};
	int x7[12] = {-1, 10, 5, 17, 23, 17, 18, -1, 3, 12, 5, 88};
	
	HeapSort(x6, 9);
	HeapSort(x7, 12);

	return 0;
}