机器学习（四）——朴素贝叶斯

最新推荐文章于 2025-04-22 22:36:50 发布

原创

最新推荐文章于 2025-04-22 22:36:50 发布

· 750 阅读

3 ·

版权

文章标签：

#机器学习 #朴素贝叶斯算法 #python

本文深入介绍了朴素贝叶斯算法，通过实例讲解其在文本分类中的应用，包括从文本中构建词向量、训练算法、过滤垃圾邮件等。此外，还展示了如何使用朴素贝叶斯分类器识别博主的知识侧重点，并分析了算法的优缺点。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

使用朴素贝叶斯分类器通过博主个人博客内容辨别博主知识侧重点

引入

前面学习的内容都是要求分类器直接给出分类结果，今天学习的朴素贝叶斯可以给出一个最优的类别猜测结果，同时给出这个猜测的概率估计值。

以垃圾邮件分类为例，一封邮件通过朴素贝叶斯得到的分类结果可能会是如下结果：

没有一个准确猜测，但是会给每个猜测计算概率，最后会选取概率最大的猜测作为结果。

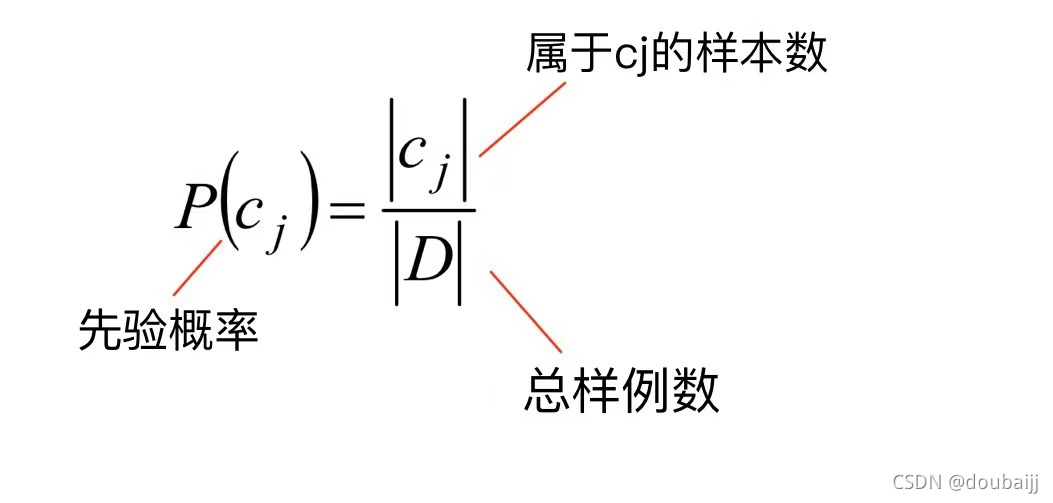
先验概率：在训练模型之前，通过历史数据得到的初始概率；该概率与待测样本无关，独立于样本。

后验概率：反映了在看到数据样本x后cj成立的置信度，即通过样本获得新的信息（既有先验概率资料，也有补充资料），利用贝叶斯公式对先验概率进行修正，而后得到的概率。

后验概率实为一个条件概率，即为已知历史数据和现有数据互不重叠的前提下，在历史数据的条件下，现有数据发生的概率

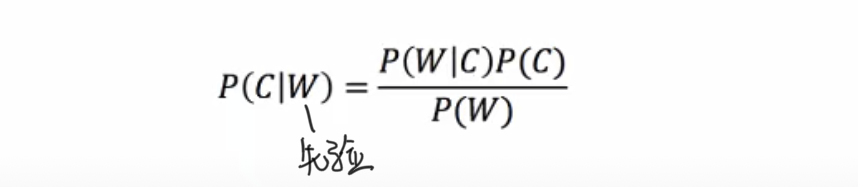
区别：先验概率只需要简单地计算，没有用到贝叶斯公式；而后验概率的计算，要用到贝叶斯公式，而且在利用样本资料计算逻辑概率时，还要使用理论概率分布，需要更多的数理统计知识。

注意：大部分机器学习模型尝试得到后验概率

生成式模型和判别式模型

机器学习可以分为两大视角，分别是生成式模型和判别式模型，本次的朴素贝叶斯是生成式模型的典型代表。

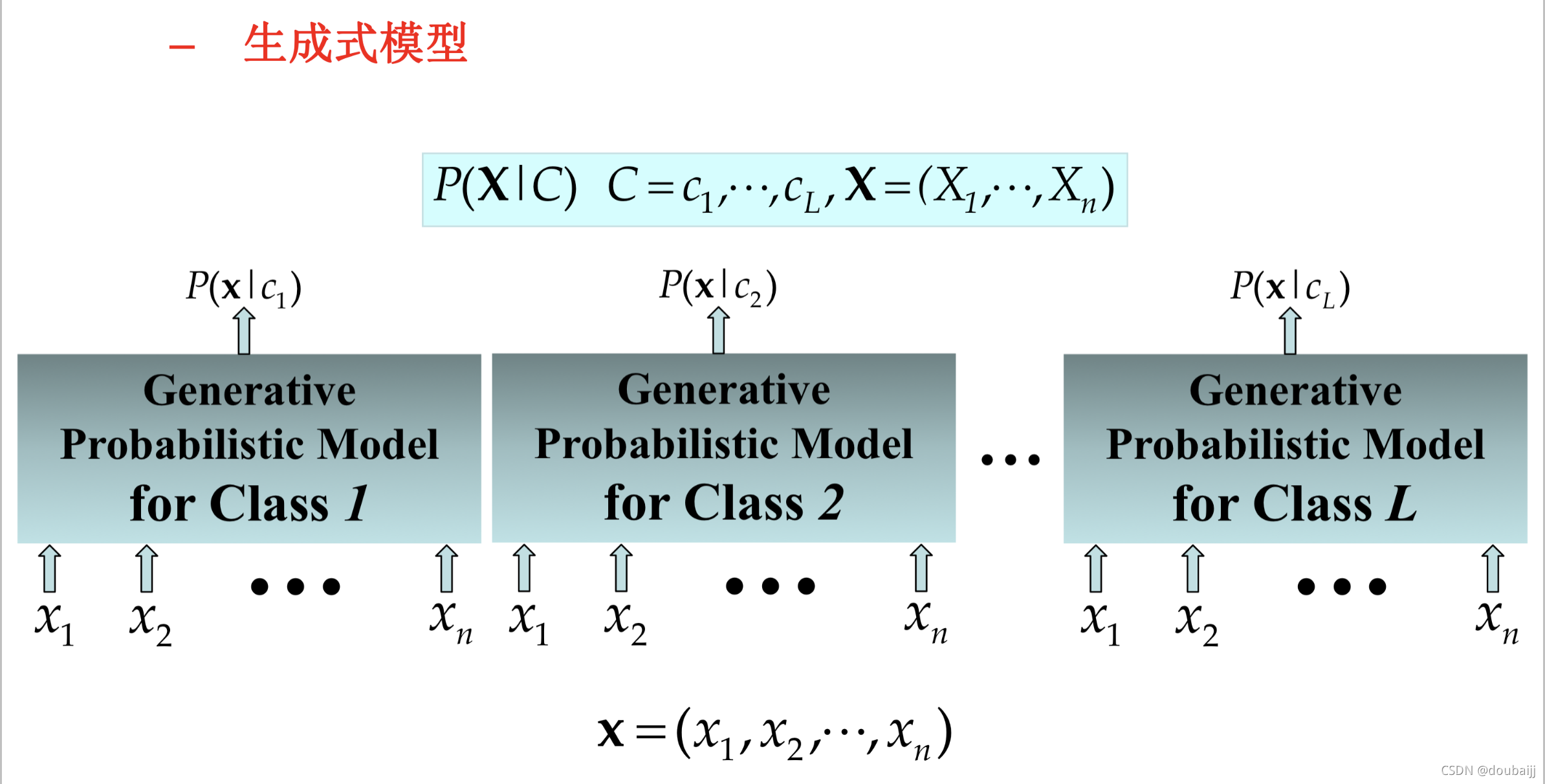
生成式模型是对联合概率P(Di,X)建立函数映射关系。

判别式模型是对条件概率P(Di|X)建立函数映射关系，该模型在学习过程中会生成一个显式决策边界，当待测样本的数据（耦合地包含了决策条件）落入某个边界，则意味着该数据属于这个类别。

举个我能理解的栗子：如何确定一只羊是山羊还是绵羊。

生成式模型：该模型会从训练数据中分别学习出一个山羊模型和一个绵羊模型，然后从待测的🐏样本里提取特征，将特征分别扔进两个模型中并计算条件概率和，哪个概率和大，🐏就属于哪个模型。

判别式模型：该模型会从训练数据中分别提取并学习绵羊和山羊的特征并生成参数，这些参数耦合地包含了区别两种羊的决策条件，然后从待测的🐏样本里提取特征，把特征投入判别式模型直接判别结果。

可以看出，在分类的过程中，生成式模型会产生多个猜测结果模型，生成式模型将从待测样本中提取到的特征分别扔入每个猜测结果模型，遍历完一遍后取概率最大的猜测模型为最终结果，而判别式模型是特征通过唯一一个模型提取得到最终结果。

朴素贝叶斯实例（了解三大知识点）

直接从公式、定理中理解朴素贝叶斯对我来说没有记忆点，所以我从一个实例问题入手。

利用朴素贝叶斯算法对文本分类：

第一步：根据问题写出两个条件概率的表达式，分别代表c是China类和c非China类：

第二步：根据条件概率定理把上式展开：

（知识点一）朴素贝叶斯之所以朴素，是因为假设了特征与特征之间是相互独立的。在这里就可以很好地应用它朴素的特性，特征之间相互独立，求各个特征的联合概率时就是将各个概率直接相乘。

因此，以下两式相等：

这样我们就可以更简单地求解第一步得到的概率表达式，由题易得：P(C)=3/4,P(Chinese|C)=5/8.但是这时可以发现P(Tokyo|C)为零，这个0直接导致了整个概率变成了0，这里就可以引入

（知识点二）——拉普拉斯修正。

别看这个公式长得难看，其实是很好用的，将这个为0的概率，分子加1，分母加上Tokyo这个数据类型的可能取值的数量，即文档中出现的各不相同的词的数量（Chinese、Beijing、Shanghai、Macao、Tokyo、Japan）共6个，因此：

P(Tokyo|C)=0/8 ==>P(Tokyo|C)=(0+1)/(8+6) =1/14

同样，原本为0的P(Japan|C)=1/14，而不为零的P(Chinese|C)也需要进行拉普拉斯修正：P(Chinese|C)=3/7

第三步：还有下列这个概率表达式（c非China类）

同样根据条件概率定理把上式展开：

可以发现（知识点三）这个概率式的分母和第一步的概率式展开后的式子分母相同，因此概率表达式的分母对决策结果没有影响，在计算比较两个概率的时候，只需要计算表达式的分子，再次简化了计算过程。

最后的答案已经不重要了，重要的是我从这个实例中较好地理解了三个知识~

朴素贝叶斯相关代码理解

这是一个常见的朴素贝叶斯的应用——文档分类。

使用Python进行文本分类

从文本中构建词向量

def loadDataSet():
    postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                 ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                 ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                 ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                 ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                 ['quit', 'buying', 'worthless', '

最低0.47元/天解锁文章