已知二叉树的中序遍历和前序遍历，如何求后序遍历

已知二叉树的中序遍历和前序遍历，如何求后序遍历

(昨晚HULU的笔试题之一，被鄙视的惨，面对向往已久的公司，交出苍白无力的答卷，心里像被剜了一刀。再多解释都是苍白。我鄙视我自己。现在开始舔舐伤口。)

假设有棵树，长下面这个样子，它的前序遍历，中序遍历，后续遍历都很容易知道。

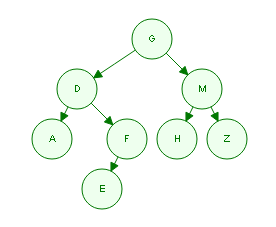
PreOrder:         GDAFEMHZ

InOrder:            ADEFGHMZ

PostOrder:       AEFDHZMG

 

现在，假设仅仅知道前序和中序遍历，如何求后序遍历呢？比如，已知一棵树的前序遍历是”GDAFEMHZ”，而中序遍历是”ADEFGHMZ”应该如何求后续遍历?

 

第一步，root最简单，前序遍历的第一节点G就是root。

 

第二步，继续观察前序遍历GDAFEMHZ，除了知道G是root，剩下的节点必然是root的左右子树之外，没法找到更多信息了。

 

第三步，那就观察中序遍历ADEFGHMZ。其中root节点G左侧的ADEF必然是root的左子树，G右侧的HMZ必然是root的右子树。

 

第四步，观察左子树ADEF，左子树的中的根节点必然是大树的root的leftchild。在前序遍历中，大树的root的leftchild位于root之后，所以左子树的根节点为D。

 

第五步，同样的道理，root的右子树节点HMZ中的根节点也可以通过前序遍历求得。在前序遍历中，一定是先把root和root的所有左子树节点遍历完之后才会遍历右子树，并且遍历的右子树的第一个节点就是右子树的根节点。

如何知道哪里是前序遍历中的左子树和右子树的分界线呢？通过中序遍历去数节点的个数。

在上一次中序遍历中，root左侧是A、D、E、F，所以有4个节点位于root左侧。那么在前序遍历中，必然是第1个是G，第2到第5个由A、D、E、F过程，第6个就是root的右子树的根节点了，是M。

 

第六步，观察发现，上面的过程是递归的。先找到当前树的根节点，然后划分为左子树，右子树，然后进入左子树重复上面的过程，然后进入右子树重复上面的过程。最后就可以还原一棵树了。

第七步，其实，如果仅仅要求写后续遍历，甚至不要专门占用空间保存还原后的树。只需要稍微改动第六步，就能实现要求。仅需要把第六步的递归的过程改动为如下:

1 确定根,确定左子树，确定右子树。

2 在左子树中递归。

3 在右子树中递归。

4 打印当前根。

 

 

PS:已知中序，后序，求前序:后序最后一个是头结点，再根据中序中头节点划分开左右子树，

参考了一些网上的讨论，具体程序是:

[cpp] view plain copy print ?

1. // InPre2Post.cpp : Defines the entry point for the console application.  
2.   
3. #include "stdafx.h"   
4. #include <iostream>   
5. using namespace std;  
6.   
7.   
8. struct TreeNode  
9. {  
10.   struct TreeNode* left;  
11.   struct TreeNode* right;  
12.   char  elem;  
13. };  
14.   
15.   
16. TreeNode* BinaryTreeFromOrderings(char* inorder, char* preorder, int length)  
17. {  
18.   if(length == 0)  
19.     {  
20.       return NULL;  
21.     }  
22.   TreeNode* node = new TreeNode;//Noice that [new] should be written out.  
23.   node->elem = *preorder;  
24.   int rootIndex = 0;  
25.   for(;rootIndex < length; rootIndex++)//a variation of the loop  
26.     {  
27.       if(inorder[rootIndex] == *preorder)  
28.       break;  
29.     }  
30.   node->left = BinaryTreeFromOrderings(inorder, preorder +1, rootIndex);  
31.   node->right = BinaryTreeFromOrderings(inorder + rootIndex + 1, preorder + rootIndex + 1, length - (rootIndex + 1));  
32.   cout<<node->elem<<endl;  
33.   return node;  
34. }  
35.   
36.   
37.   
38.   
39. int main(int argc, char* argv[])  
40. {  
41.     printf("Hello World!\n");  
42.     char* in="DBEAFCGA";  
43.     char* pr="ABDECFGA";  
44.     BinaryTreeFromOrderings(in, pr, 8);  
45.     printf("\n");  
46.     return 0;  
47. }  

// InPre2Post.cpp : Defines the entry point for the console application.

#include "stdafx.h"
#include <iostream>
using namespace std;


struct TreeNode
{
  struct TreeNode* left;
  struct TreeNode* right;
  char  elem;
};


TreeNode* BinaryTreeFromOrderings(char* inorder, char* preorder, int length)
{
  if(length == 0)
    {
      return NULL;
    }
  TreeNode* node = new TreeNode;//Noice that [new] should be written out.
  node->elem = *preorder;
  int rootIndex = 0;
  for(;rootIndex < length; rootIndex++)//a variation of the loop
    {
      if(inorder[rootIndex] == *preorder)
      break;
    }
  node->left = BinaryTreeFromOrderings(inorder, preorder +1, rootIndex);
  node->right = BinaryTreeFromOrderings(inorder + rootIndex + 1, preorder + rootIndex + 1, length - (rootIndex + 1));
  cout<<node->elem<<endl;
  return node;
}




int main(int argc, char* argv[])
{
    printf("Hello World!\n");
    char* in="DBEAFCGA";
    char* pr="ABDECFGA";
    BinaryTreeFromOrderings(in, pr, 8);
    printf("\n");
    return 0;
}

其实上面的代码写得不够简洁。题目只要求输出后续遍历，并没有要求建树。所以，不需要去计算出node->left与node->right，也不需要去return node。改进版本如下

[cpp] view plain copy print ?

1. struct TreeNode  
2. {  
3.   struct TreeNode* left;  
4.   struct TreeNode* right;  
5.   char  elem;  
6. };  
7.   
8. void BinaryTreeFromOrderings(char* inorder, char* preorder, int length)  
9. {  
10.   if(length == 0)  
11.     {  
12.       //cout<<"invalid length";   
13.       return;  
14.     }  
15.   TreeNode* node = new TreeNode;//Noice that [new] should be written out.  
16.   node->elem = *preorder;  
17.   int rootIndex = 0;  
18.   for(;rootIndex < length; rootIndex++)  
19.     {  
20.       if(inorder[rootIndex] == *preorder)  
21.       break;  
22.     }  
23.   //Left   
24.   BinaryTreeFromOrderings(inorder, preorder +1, rootIndex);  
25.   //Right   
26.   BinaryTreeFromOrderings(inorder + rootIndex + 1, preorder + rootIndex + 1, length - (rootIndex + 1));  
27.   cout<<node->elem<<endl;  
28.   return;  
29. }  
30.   
31.   
32. int main(int argc, char* argv[])  
33. {  
34.     printf("Hello World!\n");  
35.     char* pr="GDAFEMHZ";  
36.     //为什么这里不用写成char * in= new char[7];或者，可否改写为char * in= new char[7]; in="ABCDEFG";  
37.     char* in="ADEFGHMZ";  
38. //  char* in= new char[8];    
39. //  in="DBEAFCGA";   
40. //  char* pr= new char[8];    
41. //  pr="ABDECFGA";   
42.     
43.     BinaryTreeFromOrderings(in, pr, 8);  
44.   
45.     printf("\n");  
46.     return 0;  
47. }