原根(详解+代码实现+例题+快速求解一个数的原根)

1.原根定义

假设一个数g对于P来说是原根，那么g^i mod P的结果两两不同,且有 1<g<P, 1<i<P,那么g可以称为是P的一个原根

简单来说，g^i mod p ≠ g^j mod p （p为素数）

其中i≠j且i, j介於1至(p-1)之间

则g为p的原根。

 

简单的来说，如果g是P的原根，那么g的（1...P-1）次幂mod P的结果一定互不相同。

 

那么简化一下：

首先看一下欧拉定理：

欧拉定理（也称费马-欧拉定理或欧拉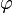函数定理）是一个关于同余的性质。欧拉定理表明，若为正整数，且互素（即），则

因此，在 时，定义 对模的指数 为使 成立的最小的正整数 。由前知  一定小于等于  ，若 ，则称 是模的原根。

 

归根到底，如果g是P的原根，就是g^(P-1) = 1 (mod P)当且仅当指数为P-1的时候成立.(这里P是素数).

 

 

 

例如：

设 m= 7，则φ（7）等于6。φ（7）表示7的欧拉函数。

设 a= 2，由于2^3=8≡1(mod 7)，而3<6，所以 2 不是模 7 的一个原根。设 a= 3，由于3^1≡3(mod 7)，3^2≡2(mod 7)，3^3≡6(mod 7)，3^4≡4(mod 7)，3^5≡5(mod 7)，3^6≡1(mod 7)，所以 3 是模 7 的一个原根。

 

2.如何求解：

一、枚举

从2开始枚举，然后暴力判断g^(P-1) = 1 (mod P)是否当且当指数为P-1的时候成立

而由于原根一般都不大，所以可以暴力得到.

二、讲究方法

例如求任何一个质数x的任何一个原根，一般就是枚举2到x-1，并检验。有一个方便的方法就是，求出x-1所有不同的质因子p1,p2...pm，对于任何2<=a<=x-1,判定a是否为x的原根，只需要检验a^((x-1)/p1),a^((x-1)/p2),...a^((x-1)/pm)这m个数中，是否存在一个数mod x为1，若存在，a不是x的原根，否则就是x的原根。

原来的复杂度是O(P-1)，现在变成O(m)*log（P-1）m为x-1质因子的个数。很明显质因子的个数远远小于x-1。

证明可用欧拉定理和裴蜀定理：

裴蜀定理

说明了对任何整数a、b和它们的最大公约数d，关于未知数x和y的线性丢番图方程（称为裴蜀等式）：

ax + by = m 
有解当且仅当m是d的倍数。裴蜀等式有解时必然有无穷多个整数解，每组解x、y都称为裴蜀数，可用辗转相除法求得。

例如，12和42的最大公因子是6，则方程12x + 42y = 6有解。事实上有(-3)×12 + 1×42 = 6及4×12 + (-1)×42 = 6。

特别来说，方程 ax + by = 1 有解当且仅当整数a和b互素。

裴蜀等式也可以用来给最大公约数定义：d其实就是最小的可以写成ax + by形式的正整数。这个定义的本质是整环中“理想”的概念。因此对于多项式整环也有相应的裴蜀定理。

证明

[html]  view plain  copy

1. 若存在，那么显然的事情  
2.   
3. 否则，假设存在一个t<phi(x)=x-1使得a^t = 1 (mod x)  
4.   
5. 那么由裴蜀定理，一定存在一组k,r使得kt=(x-1)r+gcd(t,x-1)  
6.   
7. 而由欧拉定理有，a^(x-1) = 1 (mod x)  
8.   
9. 于是1 = a^(kt) = a^(xr-r+gcd(t,x-1)) = a^gcd(t,x-1) (mod x)  
10.   
11. 而t<x-1故gcd(t,x-1)<x-1  
12.   
13. 又gcd(t,x-1)|x-1 于是gcd(t,x-1)必整除(x-1)/p1,(x-1)/p2...(x-1)/pm其中至少一个，设其一为(x-1)/pi  
14.   
15. 那么a^((x-1)/pi) = (a^gcd(t,x-1))^s = 1^s = 1 (mod x)  
16.   
17. 这与假设矛盾  

代码：

来至http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1135的一道题目：

题目

设m是正整数，a是整数，若a模m的阶等于φ(m)，则称a为模m的一个原根。（其中φ(m)表示m的欧拉函数）

给出1个质数P，找出P最小的原根。

Input

<span id="Showjim86_bnbbbsbl_s39"></span>输入1个质数P(3 <= P <= 10^9)<span id="Showjim86_bnbbbsbl_e39"></span>

Output

<span id="Showjim86_bnbbbsbl_s40"></span>输出P最小的原根。

解答

[cpp]  view plain  copy

1. #include <iostream>  
2. #include <cstdlib>  
3. #include <cstring>  
4. #include <cstdio>  
5. using namespace std;  
6. int P;  
7. const int NUM = 32170;  
8. int prime[NUM/4];  
9. bool f[NUM];  
10. int pNum = 0;  
11. void getPrime()//线性筛选素数  
12. {  
13.     for (int i = 2; i < NUM; ++ i)  
14.     {  
15.         if (!f[i])  
16.         {  
17.             f[i] = 1;  
18.             prime[pNum++] = i;  
19.         }  
20.         for (int j = 0; j < pNum && i*prime[j] < NUM; ++ j)  
21.         {  
22.             f[i*prime[j]] = 1;  
23.             if (i%prime[j] == 0)  
24.             {  
25.                 break;  
26.             }  
27.         }  
28.     }  
29. }  
30. __int64 getProduct(int a,int b,int P)//快速求次幂mod  
31. {  
32.     __int64 ans = 1;  
33.     __int64 tmp = a;  
34.     while (b)  
35.     {  
36.         if (b&1)  
37.         {  
38.             ans = ans*tmp%P;  
39.         }  
40.         tmp = tmp*tmp%P;  
41.         b>>=1;  
42.     }  
43.     return ans;  
44. }  
45.   
46. bool judge(int num)//求num的所有的质因子  
47. {  
48.     int elem[1000];  
49.     int elemNum = 0;  
50.     int k = P - 1;  
51.     for (int i = 0; i < pNum; ++ i)  
52.     {  
53.         bool flag = false;  
54.         while (!(k%prime[i]))  
55.         {  
56.             flag = true;  
57.             k /= prime[i];  
58.         }  
59.         if (flag)  
60.         {  
61.             elem[elemNum ++] = prime[i];  
62.         }  
63.         if (k==1)  
64.         {  
65.             break;  
66.         }  
67.         if (k/prime[i]<prime[i])  
68.         {  
69.             elem[elemNum ++] = prime[i];  
70.             break;  
71.         }  
72.     }  
73.     bool flag = true;  
74.     for (int i = 0; i < elemNum; ++ i)  
75.     {  
76.         if (getProduct(num,(P-1)/elem[i],P) == 1)  
77.         {  
78.             flag = false;  
79.             break;  
80.         }  
81.     }  
82.     return flag;  
83. }  
84. int main()  
85. {  
86.       
87.     getPrime();  
88.     while (cin >> P)  
89.     {  
90.         for (int i = 2;;++i)  
91.         {  
92.             if (judge(i))  
93.             {  
94.                 cout << i<< endl;  
95.                 break;  
96.             }  
97.         }  
98.     }  
99.     return 0;  
100. }