二叉树的层序打印

void LevelPrint(BinTree BT)
{/*
    首先：每一层上总的宽度应该保持相等。这是因为树是对称的。 
    其次，树的最大宽度，也就是最低层上最多可能的叶结点数，由树的层数或高度H决定。 
        最底层的最多结点数为：n=2^(H-1).
        但在打印树时，宽度还受，printf中数据的宽度，一层中数据间的间隔有关。 
   其次，对于每一层上的空间，我们认为，它是以其上每个结点为中心，平均分布的。
        也就是说，每个结点所占的空间是一样的。
        即包含：1、相同的结点数据宽度box（printf打印时需要设置） 
                2、结点左右除去自身数据外，所占有左右两个空间（即）是相同的, dis_left = dis_right = dis。
    再次，第i层上结点最多为ni = 2^(i-1)。那打印时，每层的宽度可表示为：
    
        2^(level-1) (box + 2 * dis) = Length;
        
        上式中，Length, box, 是需要在计算前确定的，level和dis是变量。
    同时，在确定Length时，需要知道树的高度，即level最大值。
        此时，只要确定一个dis就可确定打印时树的宽度。
        这个dis在选取时，应该大于0。这是因为在最底层上两个同父结点，
        如果没有一定间距，那么其父结点打在屏上时，必然后错开。         
    最后，在代码实现上，在以一定宽度打印结点数据时，要在结点数据打印前，先printf空格 dis个。
    同样在打印结点数据后，也要把空格printf dis个。这保证了结点数据在自身空间里的对称性。 
    
    如此所得的树，保持很好的对称性。 
    */
    
    if (!BT)    return;
    BinTree Tmp;
    int box = 2;                //打印时，结点数值自身宽度设定，在printf中 需要要设定为偶数。 因为它参与了后面dis的计算，被2整除 
    int maxsize = 1000;
    Queue Q = CreateQueue(maxsize);    
    AddQ(Q, BT);                //根结点入栈 
    
    int level = 1;
    /* 记录当前和下一层结点数 */
    int current_level_nodes = 1;        
    int next_level_nodes = 0;       
    
    int Height = GetHeight(BT);
    int dis = 1;                //树最大层上一个结点数据，所占有的边距 
    int Length = (int)(pow(2, Height-1)) *(box + 2 * dis);      //树的最大宽度 
    
    printf("Lenght:%d, dis:%d\n", Length, dis);
    
    dis = (Length/((int)pow(2, level-1)) - box) / 2;            //当前层上，一个结点数据的边距 
    while (level <= Height)
    {
        printf("%*c", dis, ' ');                //打印结点前，先打印其左边距 
        Tmp = DeleteQ(Q);
        if (Tmp)
        {
            printf("%*d", box, Tmp->data);      //打印结点
            AddQ(Q, Tmp->left);
            AddQ(Q, Tmp->right);
        }
        else
        {
            printf("%*c", box, ' ');            //打印空结点
            AddQ(Q, NULL);
            AddQ(Q, NULL);
        }
        
        printf("%*c", dis, ' ');                //打印结点后，再打印其右边距
        
        next_level_nodes += 2;                  //左右子树入队，下一层结点数增加2 
        --current_level_nodes;                  //因为有出队，所以当前层结点数减1 
        
        if (current_level_nodes == 0)           //更新层数、当前和下一层结点数，结点左右边距，并换行 
        {
            ++level;
            current_level_nodes = next_level_nodes;
            next_level_nodes = 0;
            
            printf("----dis:%d", dis);
            dis = (Length/((int)pow(2, level-1)) - box) / 2;
            
            printf("\n");            
        }
    }
    
}

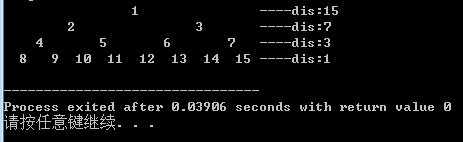
打印结果如下：

以上C程序参看了http://articles.leetcode.com/how-to-pretty-print-binary-tree/上面的部分代码。