codeforces基础题——#362（div2）D

#362（Div 2） D

题目大意： 给你一棵n个节点的树(1 <= n <= 100000)， 根结点为1， 跑一遍dfs， 但每次dfs一个点的儿子时顺序是随机的， 然后问每个点在dfs序中出现位置的期望。
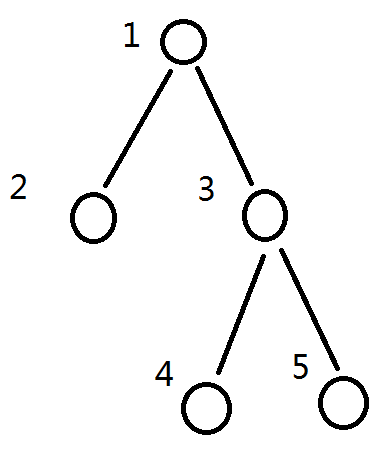
我们举个栗子：

可能的dfs序有 ： 1 2 3 4 5， 1 2 3 5 4， 1 3 4 5 2， 1 3 5 4 2
所以他们出现位置的期望分别是 ：    ( 1 + 1 + 1 + 1 ) / 4,  ( 2 + 2 + 5 + 5 ) / 4,  ( 3 + 3 + 2 + 2 ) / 4,    ( 4 + 5 + 3 + 4 )  / 4,    (5 + 4 + 4 + 3) / 4;
即 ： 1，3.5,  2.5,  4,  4 



题解 ：
这题作为D题感觉也有些水
这题第一眼反应可能有点蒙（woc， 期望， 什么玩意）， 但仔细想想其实很好算， 我们假设y是x的子节点， 假设x点位置确定， 那么枚举除y点外x的其他儿子选或不选的所有情况就是y点在dfs序中位置的所有情况，我们在选y之前选了一个点就会使y在当前dfs序中的位置加上以这个点为根的子树大小, 而这些点每一个只有选或不选两种可能，所以在所有情况中每个点会选（情况总数 / 2） 次，所以他们的贡献的和是（x除去y所有儿子的子树大小 * 情况总数 / 2）, 即期望是（x除去y所有儿子的子树大小 / 2), 即 (sz[x] - sz[y]) / 2, 
考虑dp， dp[x] = dp[father[x]] + (sz[x] - sz[father[x]]) / 2 + 1; 即可

#include <cstdio>
#include <cstring>
using namespace std;
struct Edge{
    int to, next;
}edge[100100];
int head[100100], num = -1;
void add_edge(int a, int b)
{
    edge[++ num].to = b;
    edge[num].next = head[a], head[a] = num;
}
double f[100100], sz[100100];
void dfs(int x)
{
    sz[x] = 1;
    for (int i = head[x]; i != -1; i = edge[i].next){
        dfs(edge[i].to);
        sz[x] += sz[edge[i].to];
    }
}
void dp(int x)
{
    for (int i = head[x]; i != -1; i = edge[i].next){
        f[edge[i].to] = f[x] + 1 + (sz[x] - sz[edge[i].to] - 1) / 2;
        dp(edge[i].to);
    }
}
int main()
{
    int n, x;
    scanf("%d", &n);
    memset(head, -1, sizeof(head));
    for (int i = 2; i <= n; i ++){
        scanf("%d", &x);
        add_edge(x, i);
    }
    dfs(1); //printf("*");
    f[1] = 1.0; dp(1);
    for (int i = 1; i <= n; i ++) printf("%.1lf ", f[i]);
    printf("\n");

    return 0;
}