【论文阅读】Joint consensus kernel learning and adaptive hypergraph regularization for graph-based cluster

论文地址：Joint consensus kernel learning and adaptive hypergraph regularization for graph-based clustering - ScienceDirect

代码地址：

---

摘要

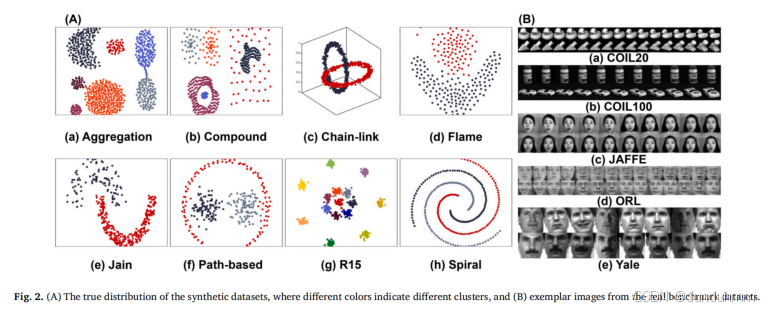
最近，多核学习（Multiple Kernel Learning，MKL）在图聚类方法中的进展展示了其从多个候选核矩阵中有效学习一致核矩阵的显著潜力。这种方法通过自表达性（self-expressiveness）在核空间中为高维数据创建低维表示。然而，如何捕获不同核矩阵中潜在的几何属性以增强数据表示，仍是一个关键挑战。在本文中，作者提出了一种新方法，称为联合一致核学习与自适应超图正则化的图聚类方法（JKHR）。方法将一种创新的自适应超图拉普拉斯正则化器（adaptive hypergraph Laplacian regularizer）引入多核学习的图聚类框架，该正则化器通过融合多个最近邻核图进行构建。JKHR方法联合并自适应地优化一致核矩阵和超图拉普拉斯正则化器，从而实现一种能够有效保留数据内在几何特性的低维表示。基于合成数据集和真实基准数据集的实验结果表明，JKHR在性能上优于最新的基于自表达性的图聚类方法以及传统的聚类技术。

引言

基于图的聚类方法因其能够稳健地处理复杂结构数据而受到广泛关注。这些方法通过将样本表示为图中的顶点，并为连接顶点对的边赋权重（反映样本之间的相似性），构建亲和图，然后利用谱或图论优化技术对图进行划分[1]。其中，归一化切割（Normalized Cut, Ncut）方法[2]是谱聚类中最广泛使用的方法。构建高质量的亲和图对准确捕捉样本之间的内在关系至关重要，这也是高效图划分的关键。传统的基于度量的方法使用特定函数（如余弦或高斯函数）来构建亲和图以衡量样本相似性。然而，这些方法严重依赖于所选的度量和超参数，特别容易受到噪声和异常值的影响[3]。近年来，开发了多种自表达图学习方法[4–14]，通过将每个样本表示为其他样本的加权组合来构建亲和图，从而有效捕捉样本间的两两关系。然而，当数据在原始特征空间中表现出非线性不可分性时，这些方法的有效性可能会受到限制[15]。

为有效处理具有非线性结构的数据，提出了基于核的自表达图学习方法，包括单核方法[15–19]和多核学习方法[19–22]。这些方法通过将非线性不可分的数据从原始特征空间映射到高维的再生核希尔伯特空间（RKHS）来构建亲和图。尽管单核方法被广泛应用，但在数据表示之前选择最优核函数和参数方面面临挑战。相比之下，多核学习方法[19,21]通过学习整合多个候选核矩阵信息的一致核矩阵，克服了这一挑战，从而实现更有效的数据表示。然而，这些多核学习方法在保留核空间中数据的局部结构信息方面仍存在局限性[20]。

在高维数据的低维表示中保留内在局部流形结构，可以显著提高亲和图的质量。图拉普拉斯正则化的自表达图学习方法[23,24]指出，当两个样本在数据的内在流形中彼此接近时，它们的表示应该在潜在的自表达系数空间中反映出这种邻近关系。这些方法部分揭示了数据的几何和拓扑特性[25–28]。然而，传统图中的每条边仅连接两个顶点，这可能无法充分捕捉数据中存在的复杂局部结构。超图拉普拉斯正则化[28]设计用于捕捉高阶关系，但构建高质量的超图仍具有挑战性。需要注意的是，在基于超图拉普拉斯正则化的自表达图聚类相关研究中，超图的构建通常基于原始特征空间中的局部空间信息或从数据自表达性中计算的相关系数[28,29]。一旦构建，超图通常是固定的，若其质量较低则难以优化。此外，目前鲜有研究将多核学习与超图嵌入整合到统一框架中以改进聚类。

本文提出了一种名为联合一致核学习与自适应超图正则化的图聚类方法（JKHR）。JKHR在基于多核学习的图聚类框架中引入了一种新颖的自适应超图拉普拉斯正则化器。该正则化器通过融合多个最近邻核图，充分利用不同候选核矩阵中的潜在几何特性，并基于数据的内在几何提取稳定的高阶关系。通过一致核矩阵和超图拉普拉斯正则化器的联合优化，实现两者的相互指导和动态增强。结果表明，在数据空间内在几何中接近的样本具有相似的低维表示，从而生成高质量的亲和图。

本文的主要贡献包括：

1. 自适应超图拉普拉斯正则化器：提出了一种新颖的自适应超图拉普拉斯正则化器，可自动融合多个最近邻核图，利用核矩阵的潜在几何特性以及超图捕捉数据内在高阶关系的能力。
2. 多核学习中的联合优化：将自适应超图拉普拉斯正则化器引入多核学习的图聚类中，实现一致核矩阵与超图拉普拉斯正则化器的联合优化与相互增强，从而生成高质量的亲和图，保留数据的内在几何结构，提高聚类性能。
3. 有效的优化框架：基于交替方向乘子法（ADMM），设计了一种有效的优化框架，用于联合优化一致核矩阵和超图拉普拉斯正则化器。
4. 全面的实验验证：在八个合成数据集和五个真实基准数据集上进行广泛实验，结果表明，所提出的方法相比九种最新的自表达图聚类方法和两种传统聚类方法具有更优越的性能。

模型

 联合共识核学习与自适应超图正则化的图聚类方法（JKHR） 的关键特性在于，在优化过程中，核空间中的数据自表达性、共识核学习和超图拉普拉斯正则化之间的相互指导与动态增强，而不是简单地将这些元素结合起来。其核心包括一种通过融合多个近邻核图生成的新颖超图拉普拉斯正则化方法，能够准确捕捉并保留数据高维空间中的内在几何特性，从而提升关联图的质量。此外，JKHR 利用多核学习来最大化基于核的自表达性关联图的优势。JKHR 的框架如图 1 所示。

基于多近邻核图融合的新型超图拉普拉斯正则化方法

与普通图相比，高质量的超图能够提供更丰富且更准确的样本关系。超图拉普拉斯正则化在保留复杂数据的流形结构信息方面起着关键作用。Yin 等人提出了一种超图拉普拉斯正则化方法，其中构建的超图中，每条超边包含具有相同属性值的样本【28】。类似地，Xu 等人使用超图拉普拉斯正则化方法，在其中基于原始数据的谱欧几里得距离构建了一个 k-近邻超图【29】。

然而，这些超图是基于原始数据构建的，并未在数据重建过程中进行优化。这一限制可能会妨碍对数据潜在几何特性的充分利用，并在低维表示中难以有效保留这些特性，尤其是在处理包含噪声和异常值的高维数据时。

为了提升超图拉普拉斯正则化器的有效性，作者提出通过融合多个从不同候选核矩阵获得的最近邻核图来构建超图，从而形成一种新型超图拉普拉斯正则化器。该超图利用多个核矩阵的潜在几何特性提取数据中稳定的高阶内在关系，并通过多核学习的整合实现连续优化。这种方法与现有的固定超图拉普拉斯正则化器形成鲜明对比。以下是作者提出的新型超图拉普拉斯正则化器的详细说明：

给定包含 n 个样本的 d-维数据矩阵 X=[x1,x2,…,xn]和 m 个候选核矩阵 ，其中 Hio，我们首先构建 m 个最近邻核图 {Gik}。最近邻核图 Gik(V,Eik)的邻接矩阵 Hik定义如下：

其中，{Hio}i对应不同类型的核函数（如线性核、多项式核和高斯核）及其参数。V={v1,v2,…,vn}表示 n 个样本的顶点，Nk(vi)表示基于 Hio\ 的 vi 的 k个最近邻集合。通过这种方式，最近邻核图保留了每个顶点与其 k个最近邻之间的关系。

然后，通过融合多个最近邻核图 {Gik}，得到图 G(V,E)。其邻接矩阵 S表示为：

其中权重向量 g=[g1,g2,…,gm]⊤对应候选核矩阵 {Hio}。

最终，基于融合后的图 G(V,E)构建超图 G(V,E,Ψ)，其概率关联矩阵定义为：

其中，s^表示融合图 G(V,E)中所有边权的平均值。与典型的（0,1）关联矩阵不同，概率关联矩阵表示顶点属于超边的概率。此外，超边 ej的权重 w(ej)定义为：

其中 是子矩阵，包含 SO 中对应 Ωej行和列的元素。超边权重 w(ej)表示超边中顶点对之间所有亲和性的总和，这些亲和性来源于融合的候选核矩阵。这样构建的超图能够充分捕获样本之间的关系，每个超边权重准确反映其在超图中的重要性。

基于构建的超图 G(V,E,Ψ)，制定了非归一化的超图拉普拉斯正则化器，表达式如下：

归一化后的 Lh 表达为：

从而得到归一化的超图拉普拉斯正则化器：

需要注意的是，作者通过将超图拉普拉斯正则化器与多核学习相结合，实现了正则化器的自适应优化。

联合共识核学习与自适应超图正则化的图聚类方法

现有基于多核学习的图聚类方法通过从多个候选核矩阵中学习共识核，以最小化核空间中的数据重构误差，从而构建相似性图。然而，这些方法通常忽略了诸如流形结构等有价值信息的保留。为了解决这一问题，作者提出了JKHR方法，它结合了超图拉普拉斯正则化器与基于多核学习的图聚类方法。首次联合优化共识核矩阵与超图拉普拉斯正则化器，从而在核空间中生成具有更强表示能力的自表达相似性图，提高聚类性能。

与作者的方法最接近的是Kang等人提出的方法[21]，但其方法未考虑利用图或超图拉普拉斯正则化来加强自表达相似性图中数据固有几何特性的保留。

JKHR方法的公式：

其中，

• Z=[z1,z2,⋯ ,zn] 是系数矩阵，zi表示通过数据自表达在核空间中对样本 xi的低维映射；
• K是学习得到的共识核矩阵；
• g=[g1,g2,⋯ ,gm]T 是与候选核矩阵 {Hio}对应的权重向量；
• Lhsym是归一化的超图拉普拉斯矩阵；
• α,β,γ,δ 是用于平衡各项的惩罚参数。

公式 (14) 的各项解释如下：

1. 第一项 Tr(K−2KZ+ZTKZ)：表示核空间中数据的自表达拟合，用于捕捉全局的重构关系。
2. 第二项 ρ(Z)：是对系数矩阵 Z的正则化，将结构假设编码到其中以捕捉数据的潜在结构。本方法中，ρ(Z) 使用稀疏正则化 ∥Z∥ 或低秩正则化 ∥Z∥∗。
   • ∥Z∥1：使学习到的 Z尽可能稀疏，即样本由尽可能少的样本表示。
   • ∥Z∥∗：使 Z尽可能低秩，从而减少噪声的影响并提高表示能力。
3. 第三项 ∥K∥∗：是对共识核矩阵 K的低秩正则化。
4. 第四项 ：用于从所有候选核矩阵的线性组合中学习最优的共识核矩阵。
5. 最后一项 Tr(ZLhsymZT)：是超图拉普拉斯正则化器，在 Lhsym的指导下保留 Z 中数据的固有几何结构。确保在固有几何中彼此接近的样本具有相似的低维表示。

与以往固定的超图拉普拉斯正则化器不同，JKHR在核空间中的数据重构过程中动态更新超图拉普拉斯正则化器。具体来说，超图是通过融合从候选核矩阵 {Hio}得到的多个最近邻核图构造的，其融合权重与共识核学习得到的候选核矩阵权重 g=[g1,g2,⋯ ,gm]T相同。超图拉普拉斯正则化器增强了 Z中固有几何的保留。

实验

---

虽然是一个传统方法，但是思想和创新点还是可以学习借鉴的。。。