算术表达式转成前缀表达式（波兰表达式）并求值

    上一篇文章，楼主分享了自己如何将一个中缀表达式转化成后缀表达式并求值，在这篇文章当中楼主将介绍如何将一个中缀表达式转换成一个前缀表达式并求值。并且在文章的末尾楼主将会总结一下中缀表达式转换成前缀表达式和后缀表达式时有哪些异同点。

中缀表达式转换成前缀表达式（波兰表达式）

相信对于为什么我们需要将中缀表达式转换成前缀表达式大部分读者都已知晓其中的原因，这样做主要是为了便于计算机来处理，如果让我们人类来处理，中缀表达式更符合我们的认知习惯。那么如何将中缀表达式转换成前缀表达式呢? 下面我们将详细说明该过程的基本思路以及具体的Java代码实现。

首先，我们需要规定各个运算符的优先级，使得‘*’、‘/’优先级最高，‘+’，‘-’次之，‘）’的优先级最低（至于为什么优先级要这样设计，楼主现在也不太清楚，还是因为太菜不过很多书上都是这样设计的，就暂且先这样做吧。如果有哪位前辈明确知道其中的原因，还请不吝赐教，私信给我或者直接评论，再次先行谢过！当然，如果楼主哪天搞明白其中的原因肯定会来此更新，把经验分享给大家）。

接下来就是基本思路的介绍：

1.建立一个空栈，用来保存运算符；

2.从右至左遍历中缀表达式；

   1)如果当前字符为运算数则直接将其加入前缀表达式中。

   2)如果当前字符为运算符，此时如果栈为空则直接将其入栈，否则判断栈顶运算符的优先级是否大于当前操作符的优先级，如果是就将栈顶元素出栈       加入到前缀表达式中，直到栈为空或栈顶运算符的优先级小于等于当前运算符的优先级，最后将当前运算符加入到前缀表达式当中。

  3)如果当前字符为‘）’，则将其直接入栈。

  4)如果当前字符为‘(’ ，则将栈顶元素出栈并加入到前缀表达式当中，直到最后‘)’出栈。（注意，‘)’需要出栈当不需要加入到前缀表达式当中）。

3.遍历完中缀表达式后将栈中所有元素出栈并加入到前缀表达式中。

4.将得到的前缀表达式逆序就可以得到最终的结果。

5.代码实现在文章末尾处。

波兰表达式求值

基本思路：

1.建立一个空栈，用来保存运算数；

2.从右至左遍历前缀表达式；

  1)如果当前字符为运算数直接将其入栈；

  2)如果当前字符为运算符则将栈顶运算数出栈作为左操作数，再将栈顶运算数出栈作为右操作数，并用左操作数操作右操作数，最后将结果入              栈。

3.当遍历完整个前缀表达式，栈顶元素的值即为表达式的最终结果。

以上表述用java代码实现为：

import java.util.HashSet;
import java.util.Scanner;
import java.util.Stack;

/**
 * 
 * 该类主要用来计算数学表达式的值，中缀表达式转换成前缀表达式（波兰表达式式）并计算结果。
 * @author DW
 *
 */
public class InToPre {

	private static HashSet<Character> optr = new HashSet<Character>();		//保存操作符的集合
	//初始化操作符
	private static void initOptr() {
		optr.add('+');
		optr.add('-');
		optr.add('*');
		optr.add('/');
	}
	
	//判断字符是否为操作符
	private static boolean isOptr(char c) {
		if(optr.contains(c))
			return true;
		return false;
	}
	
	//判断字符是否为操作数
	private static boolean isOperand(char c) {
		if(c>='0'&&c<='9')
			return true;
		return false;
	}
	
	
	/*		算术表达式转换为前缀表达式的基本思想：
	 * 			1.初始化一个栈optr,用来存放运算符；
	 * 			2.从右往左扫描输入的字符串；
	 * 				3.如果遇到的是‘)’,将其直接入栈，开始下一次扫描；
	 *				4.如果遇到的是‘(’,将栈中运算符挨个弹出，送往后缀表达式中，直到遇到第一个‘)’。(注意：弹出的‘)’应当丢弃));
	 *				5.如果遇到的是运算数，直接送往前缀表达式；
	 *				6.如果遇到是运算符 , 如当前栈为空直接入栈，否则如果栈顶元素的优先级高于当前运算符，则将栈顶元素出栈并加入到前缀表达式中直到栈顶
	 *				      元素的优先级小于等于当前操作符，最后将当前操作符入栈。
	 *			8.读取完毕后将栈中所有元素出栈并加入前缀表达式当中；
	 *			9.将以上获取的前缀表达式进行逆序才能得到最终的前缀表达式。
	 *		关于运算符的优先级规定：
	 *			‘*’，‘/’	优先级为3，最高
	 *			‘+’，‘-’ 优先级为2
	 *			‘)’ 优先级为1，最低
	 *
	 */
	
	
	
	private static int priority(char c) {
		switch(c) {
			case'*':
			case'/':
				return 3;
			case'+':
			case'-':
				return 2;
			case')':
				return 1;
			default:{
				System.out.println("输入错误！");
				return 0;
			}
		}
	}
	
	
	/*			利用前缀表达式求值的基本思想：
	 * 				1.初始化一个操作数栈；
	 * 				2.从右到左遍历前缀表达式
	 * 					3.如果是操作数则直接入栈
	 *					4.如果是操作符就从栈中取两个操作数计算，然后将结果入栈
	 *				5.重复以上步骤直至前缀表达式遍历结束；
	 */
	
	public static int numberCalculate(String prefix) {
		Stack<Integer> count = new Stack<Integer>();
		char c;
		int number1,number2;
		for(int i = prefix.length() - 1; i >= 0; i--) {
			if(isOperand(c = prefix.charAt(i)))
				count.push(c - '0');
			else {
				number1 = count.pop();
				number2 = count.pop();
				switch(c) {
					case'+':
						count.push(number1 + number2);
						break;
					case'-':
						count.push(number1 - number2);
						break;
					case'*':
						count.push(number1 * number2);
						break;
					case'/':
						count.push(number1 / number2);
						break;
				}
			}
		}
		return count.pop();
	}
	
	public static void main(String[] args) {
		
		initOptr();
		Scanner scan = new Scanner(System.in);
		String expression = scan.nextLine();					//输入的表达式
		StringBuilder prefixExpr = new StringBuilder();			//保存已将建立的前缀表达式
		Stack<Character> optr = new Stack<Character>();			//操作符栈
		char c;													//输入表达式某个位置的字符
		char pop;												//运算符栈中弹出的字符
		
		for(int i = expression.length() - 1; i >= 0; i--) {
			c = expression.charAt(i);
			//如果当前字符为操作数
			if(isOperand(c)) {
				prefixExpr.append(c);
			}
			
			//如果当前字符为操作符
			else if(isOptr(c)) {
				if(optr.isEmpty())
					optr.push(c);
				else {
					while(true) {
						if(optr.isEmpty() || priority(optr.peek()) <= priority(c))
							break;
						pop = optr.pop();
						prefixExpr.append(pop);
					}
					optr.push(c);
				}
			}
			
			//如果当前字符为‘)’
			else if(')' == c) {
				optr.push(c);
			}
			
			//如果当前字符为‘(’
			else if('(' == c) {
				while((pop = optr.pop() ) != ')')
					prefixExpr.append(pop);
			}
			
			else
				System.out.println("输入得表达式有错误：=======>"+c);
		}
		while(!optr.isEmpty())
			prefixExpr.append(optr.pop());
		//将得到的表达式逆序后才是最终结果
		prefixExpr = prefixExpr.reverse();
		System.out.println("转换后的前缀表达式为："+prefixExpr.toString());
		System.out.println("前缀表达式计算的结果为："+numberCalculate(prefixExpr.toString()));
	}
	
}

程序的运行结果：

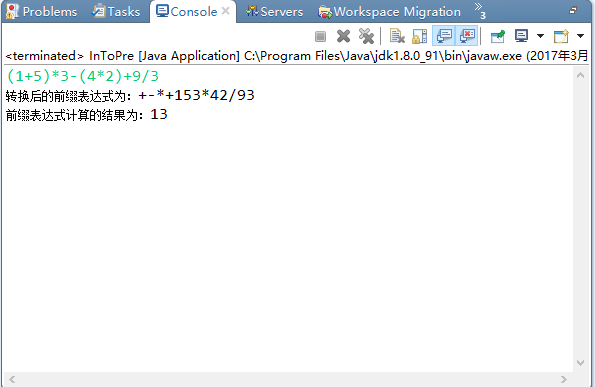
中缀表达式转前缀表达式和中缀表达式转后缀表达式的比较：

利用前缀表达式求值和利用后缀表达式求值的比较：

为什么前缀表达式先出栈的操作数为左操作数而后缀表达式先出栈的为右操作数？

一定要注意红色字体标记出来的遍历顺序！！！

由于