数字图像处理，相位相关算法解决图像的刚性平移问题

参考论文中的文字：图像配准是图像处理的基本任务之一,用于将不同时间、不同传感器、不同视角及不同拍摄条件下获取的关于同一目标或场景的两幅或多幅图像进行主要是几何意义上的匹配套和的过程。在对图像配准的研究过程中,大量技术被应用于针对不同数据和问题的图像配准工作,产生了多种不同形式的图像配准技术。

图像配准的基本问题是找出一种图像转换方法,用以纠正图像的形变。造成图像形变的原因多种多样,例如对于遥感图像而言,传感器噪声、由传感器视点变化或平台不稳定造成的透视变化、被拍摄物体的移动、变形或生长等变化、闪电和大气变化,以及阴影和云层遮盖都使图像产生不同形式的形变。正是图像形变原因和形式的不同决定了多种多样的图像配准技术。

迄今已报道了多种图像配准方法,主要有互相关法、傅立叶变换法、点映射法口脚外和弹性模型法。其中傅立叶变换法基于傅立叶变换的相位匹配是利用傅立叶变换的性质而出现的一种图像配准方法。图像经过傅立叶变换,由空域变换到频率缘则两组数据在空何上的相关运算可以变为频谱的复数乘法运算,同时图像在变换域中还能获得在空域中很难获得的特征。

一，基于相位相关的图像配准方法

在时域中信号的平移运动可以通过在频域中相位的变化表现出来（这是傅里叶变换的特性，见下图）。

平移不影响傅氏变换的幅值（谱），对应的幅值谱和原图像是一样的。旋转在傅氏变换中是小变量。根据傅氏变换的旋转特性，旋转一幅图，在频域相当于对这幅图的傅氏变换做相同的旋转。使用频域方法的好处是计算简单，速度快（可使用MIT的fftw库）,同时傅立叶变换可以采用方法提高执行的速度。因此,傅氏变换是图像配准中常用的方法之一。下面我们就具体分析当图像发生平移、旋转和缩放时,图像信号在频域中的表现。

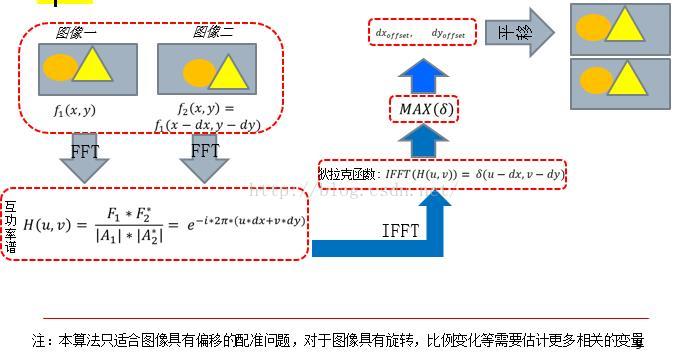
1，解决刚性平移问题的原理阐述

通过求取互功率谱的傅立叶反变换,得到一个狄拉克函数（脉冲函数）,再寻找函数峰值点对应的坐标,即可得到我们所要求得的配准点。实际上,在计算机处理中,连续域要用离散域代替,这使得狄拉克函数转化为离散时间单位冲击函数序列的形式。在实际运算中,两幅图像互功率谱相位的反变换,总是含有一个相关峰值代表两幅图像的配准点,和一些非相关峰值,相关峰值直接反映两幅图像间的一致程度。更精确的讲,相关峰的能量对应重叠区域的所占百分比,非相关峰对应非重叠区域所占百分比。由此我们可以看出,当两幅图像重叠区域较小时,采用本方法就不能检测出两幅图像的平移量。

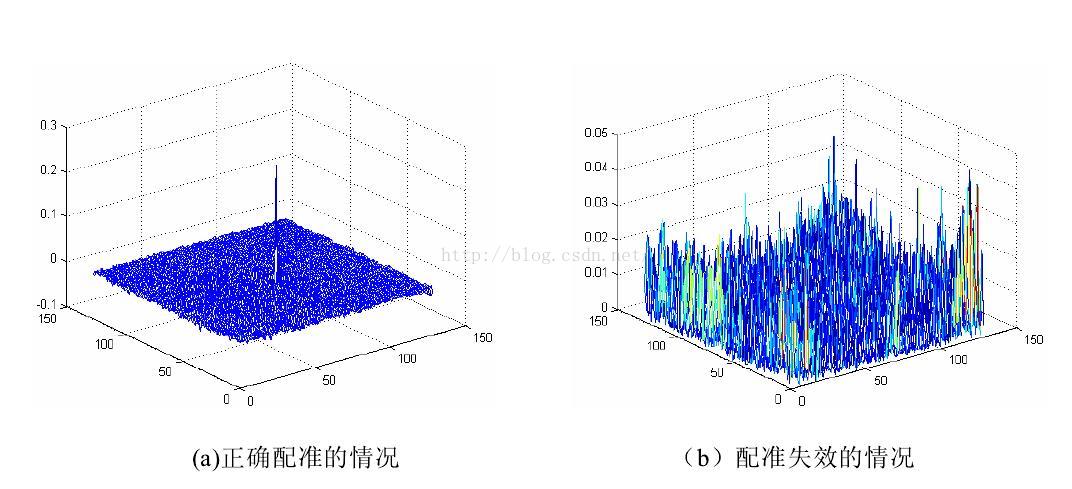
2，合理的配准情况

当图像间仅存在平移时，正确的配准图像如图a所示（中心平移化了），最大峰的位置就是两图像的相对平移量，反之若不存在单纯的平移，则会出现如b所示的情况（多脉冲林立）

3，算法流程

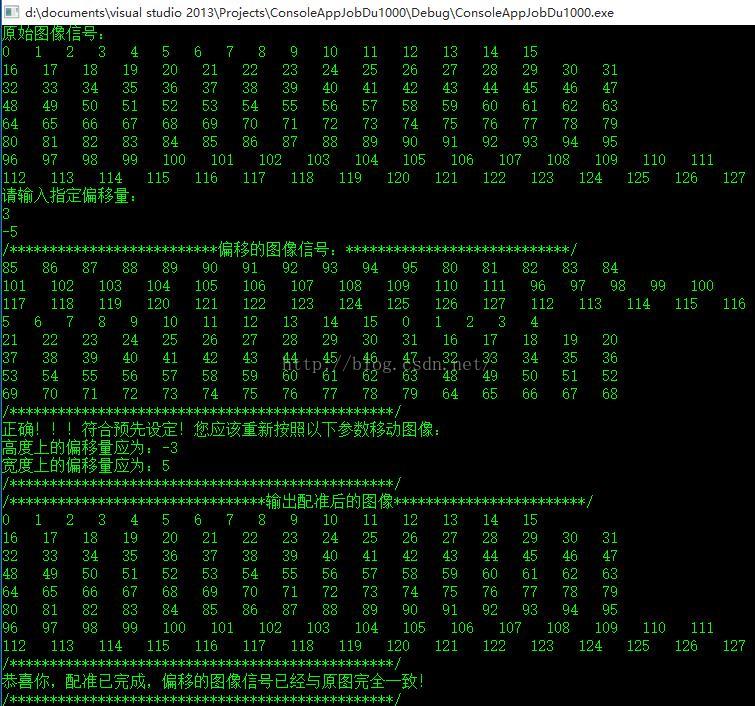
4，配准模拟结果：

1,对绝对理想的图像进行配准模拟

（代码见后面）

绝对理想的图像：图中整体的图像都没有因为平移而带来像素的损失，即再往下移动越界后像素偏移到了上面，往右移动越界后像素偏移到左边，所以图片中模拟的图像没有任何像素损失。

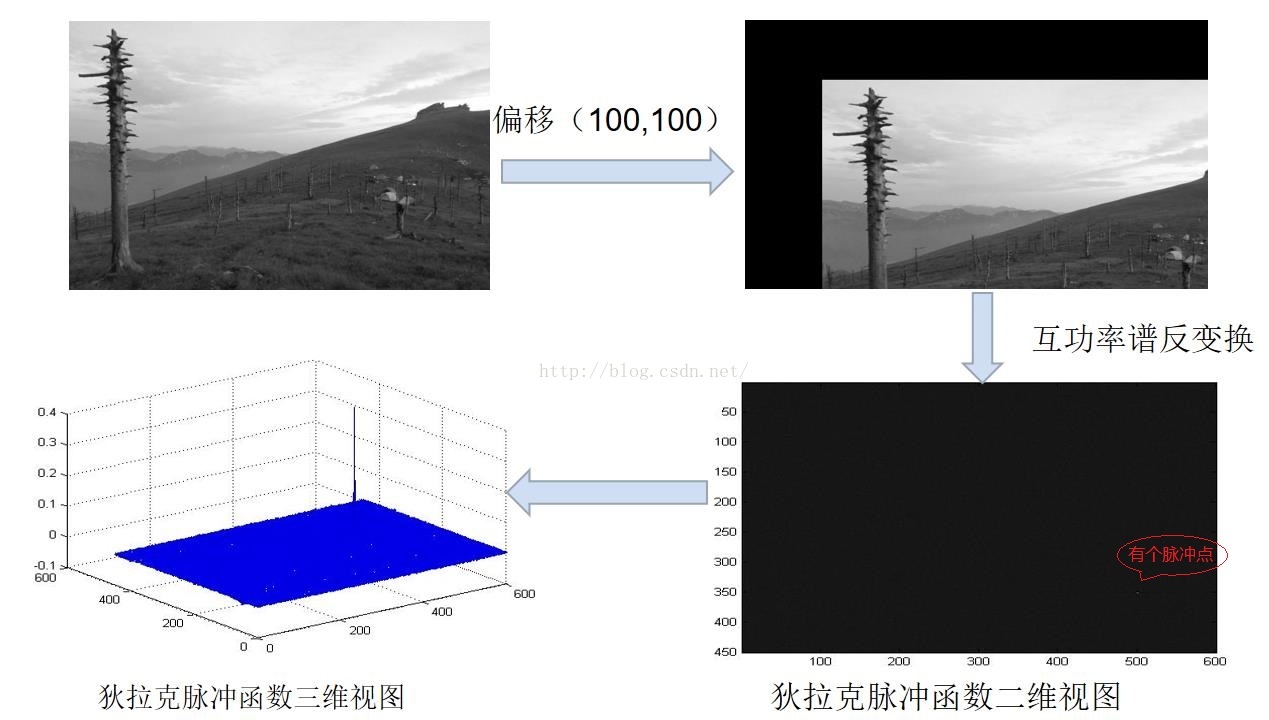
2,对带有指定偏移量的图像偏移估计

（matlab实现，代码见参考1）

本实验图像大小为600*450（其中600是宽度），可以看见成功找到了偏移量。

但是后来我想了想，这个实验中的图像平移是不严谨的，平移后图像左上方的像素变成了黑色，不过从结果来看，影响并不大，接下来换了一张更严谨的偏移实验图像：

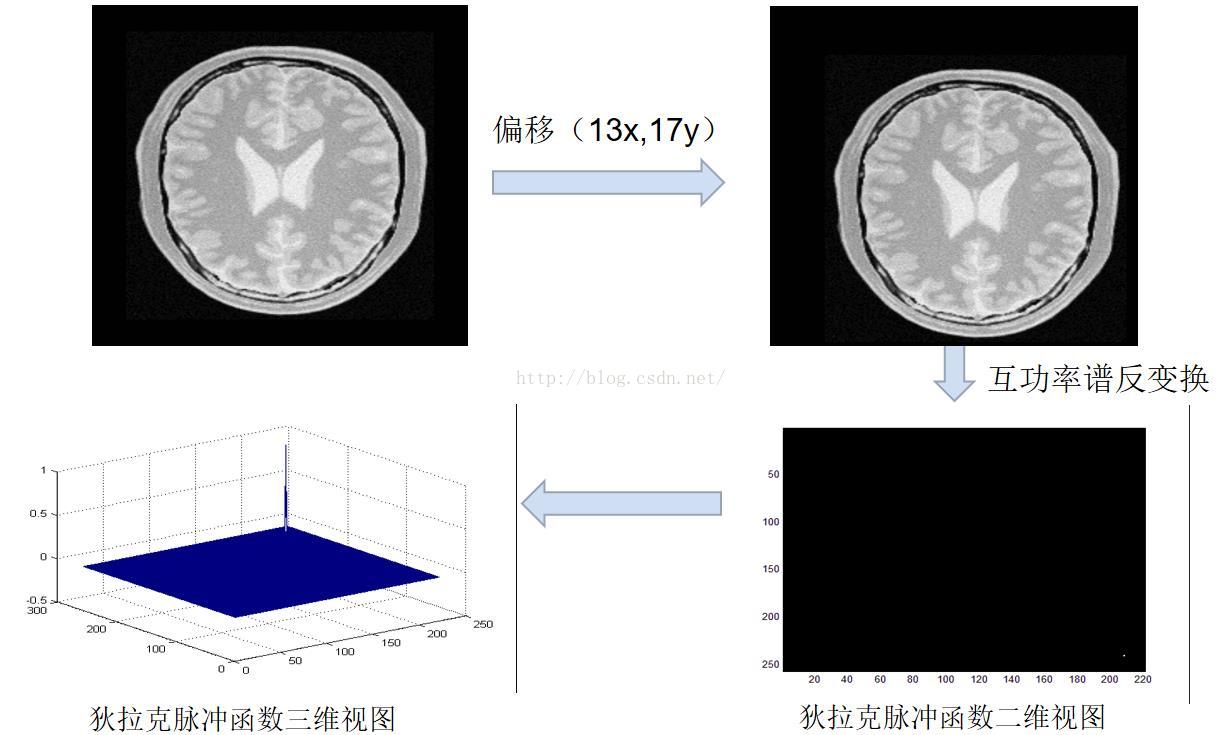
3,与OpenCV实现的库函数相比较

代码见参考2

从结果可以看出，两者基本一致，对于制定偏移量为13,17的图像，估计结果opencv还是有一点偏差，但是还是可以接受的。

但是OpenCV自己实现的phaseCorrelate()明显快很多很多很多，666666666666666666666

参考代码1：

%读取
Image1 = (imread('image_gray.jpg')); % 
Image2 = (imread('img_result_8_15.jpg')); % 带有偏移量的图像，高度向下偏移8，宽度向右偏移15

%显示
subplot(1,2,1);imshow(Image1);  title('原参考图像');
subplot(1,2,2);imshow(Image2);  title('带有偏移量的图像');

FFT1 = fft2(Image1); % 二维 FFT  
FFT2 = conj(fft2(Image2)); %共轭复数  

%求复功率谱
FFTR = FFT1.*FFT2; % 复共轭（复功率谱的分子）  
magFFTR = abs(FFTR); %sqrt(real^2 + imag^2)取模 （复功率谱的分母）
FFTRN = (FFTR./magFFTR);  

%复功率谱的反变换
result = ifft2(double(FFTRN));   

M = max(max(result));
[i,j] = find(result == M)

figure;  colormap('gray');imagesc(result);  
figure;  colormap(jet);  mesh(result);  

参考代码2：

int main(int argc, char** argv)
{
	Mat srcImage11 = imread("Brain13x17y.bmp");
	Mat srcImage21 = imread("BrainP.bmp");
	Mat dst1, dst2;
	Mat srcImage1, srcImage2;
	cvtColor(srcImage11, srcImage1, CV_BGR2GRAY);
	cvtColor(srcImage21, srcImage2, CV_BGR2GRAY);


	srcImage1.convertTo(dst1, CV_32FC1);
	srcImage2.convertTo(dst2, CV_32FC1);

	QueryPerformanceFrequency(&freq);
	QueryPerformanceCounter(&startTime);//开始计时
	Point2d phase_shift;
	phase_shift = phaseCorrelate(dst1, dst2);
	cout << "OpneCV库函数实现 :" << endl << "\tX方向的偏移 : " << phase_shift.x << ",\tY方向的偏移 : " << phase_shift.y << endl;
	QueryPerformanceCounter(&stopTime);
	time = 1e3*(stopTime.QuadPart - startTime.QuadPart) / freq.QuadPart;

	cout << "你电脑的频率为：" << freq.QuadPart << endl;
	cout << "opencv库函数消耗时间为：" << time << "毫秒" << endl;
	
	QueryPerformanceCounter(&startTime);//开始计时
	int height_offset = 0;
	int width_offset = 0;
	PhaseCorrelation2D(srcImage1, srcImage2, height_offset, width_offset);//宽的偏移量  
	cout << "Phase Correlation自实现 :" << endl << "高度偏移量" << -height_offset << ",   宽度偏移量" << -width_offset << endl;
	QueryPerformanceCounter(&stopTime);//结束计时
	time = 1e3*(stopTime.QuadPart - startTime.QuadPart) / freq.QuadPart;
	cout << "自实现相位相关函数消耗时间为：" << time << "毫秒" << endl;
	waitKey(0);
	getchar();
	return 0;
}

参考代码3（需要配置opencv库和MIT的fftw库）：

#include <stdio.h>
#include <iostream>
#include "fftw3.h"
#include "vector"

#include <opencv2/legacy/legacy.hpp>
#include <opencv2/nonfree/nonfree.hpp>//opencv_nonfree模块：包含一些拥有专利的算法，如SIFT、SURF函数源码。 
#include "opencv2/core/core.hpp"
#include "opencv2/features2d/features2d.hpp"
#include "opencv2/highgui/highgui.hpp"
#include <opencv2/nonfree/features2d.hpp>

using namespace cv;
using namespace std;

void PhaseCorrelation2D(const Mat &signal,//原图像信号
	const  Mat &pattern,//带配准图像信号
	int &height_offset,//用来获取估计的高度偏移量
	int &width_offset);//获取宽的偏移量


//本程序做了一个很简单的测试：计算“配准样图”中那些样图的偏移量
//（这些图都是通过matlab理想化的平移图）	
int main()
{
	Mat srcImage11 = imread("image_gray.jpg");
	Mat srcImage21 = imread("img_result_-8_-25.jpg");
	Mat srcImage1, srcImage2;
	cvtColor(srcImage11, srcImage1, CV_BGR2GRAY);
	cvtColor(srcImage21, srcImage2, CV_BGR2GRAY);
	
	int height_offset = 0;
	int width_offset = 0;
	PhaseCorrelation2D(srcImage1,srcImage2,height_offset,width_offset);//宽的偏移量
	cout <<"Phase Correlation法 :  高度偏移量"<< -height_offset<<"   宽度偏移量" << -width_offset << endl;
	getchar();
	return 0;
}

//该函数返回图像的刚性平移量
void PhaseCorrelation2D(const Mat &signal,//原信号
	const  Mat &pattern,//带配准信号
	int &height_offset,//高的偏移量
	int &width_offset)//宽的偏移量
{
	int nRow = signal.rows;
	int nCol = signal.cols;
	fftw_complex *signal_img = (fftw_complex*)fftw_malloc(sizeof(fftw_complex)*nRow*nCol);
	fftw_complex *pattern_img = (fftw_complex*)fftw_malloc(sizeof(fftw_complex)*nRow*nCol);

	for (int i = 0; i < nRow; i++)
	{
		for (int j = 0; j < nCol; j++)
		{
			signal_img[i*nCol + j][0] = signal.at<uchar>(i, j);
			signal_img[i*nCol + j][1] = 0;
			pattern_img[i*nCol + j][0] = pattern.at<uchar>(i, j);
			pattern_img[i*nCol + j][1] = 0;
		}
	}

	// 对两幅图像进行傅里叶变换
	fftw_plan signal_forward_plan = fftw_plan_dft_2d(nRow, nCol, signal_img, signal_img,
		FFTW_FORWARD, FFTW_ESTIMATE);
	fftw_plan pattern_forward_plan = fftw_plan_dft_2d(nRow, nCol, pattern_img, pattern_img,
		FFTW_FORWARD, FFTW_ESTIMATE);
	fftw_execute(signal_forward_plan);
	fftw_execute(pattern_forward_plan);

	// 求互功率谱
	fftw_complex *cross_img = (fftw_complex*)fftw_malloc(sizeof(fftw_complex)*nRow*nCol);
	double temp;
	for (int i = 0; i < nRow*nCol; i++)
	{
		cross_img[i][0] = (signal_img[i][0] * pattern_img[i][0]) -
			(signal_img[i][1] * (-1.0*pattern_img[i][1]));
		cross_img[i][1] = (signal_img[i][0] * (-1.0*pattern_img[i][1])) +
			(signal_img[i][1] * pattern_img[i][0]);
		temp = sqrt(cross_img[i][0] * cross_img[i][0] + cross_img[i][1] * cross_img[i][1]) + 0.001;
		cross_img[i][0] /= temp;
		cross_img[i][1] /= temp;
	}

	// backward fft，对互功率谱求反变换
	// FFTW computes an unnormalized transform,
	// in that there is no coefficient in front of
	// the summation in the DFT.
	// In other words, applying the forward and then
	// the backward transform will multiply the input by n.

	// BUT, we only care about the maximum of the inverse DFT,
	// so we don't need to normalize the inverse result.

	// the storage order in FFTW is row-order
	fftw_plan cross_backward_plan = fftw_plan_dft_2d(nRow, nCol, cross_img, cross_img,
		FFTW_BACKWARD, FFTW_ESTIMATE);
	fftw_execute(cross_backward_plan);

	// free memory
	fftw_destroy_plan(signal_forward_plan);
	fftw_destroy_plan(pattern_forward_plan);
	fftw_destroy_plan(cross_backward_plan);
	fftw_free(signal_img);
	fftw_free(pattern_img);

	double *cross_real = new double[nRow*nCol];
	for (int i = 0; i < nRow*nCol; i++)
		cross_real[i] = cross_img[i][0];
	//根据反变换求出平移量
	int max_loc = 0;//准备存放最大值的位置坐标（注意，只有一个值）
	double max_vlaue = 0.0;
	for (int i = 0; i < nRow*nCol; i++)
	{
		if (max_vlaue<cross_real[i])
		{
			max_vlaue = cross_real[i];
			max_loc = i;
		}
	}

	height_offset = (int)floor(((int)max_loc) / nCol);
	width_offset = (int)max_loc - nCol*height_offset;

	if (height_offset > 0.5*nRow)
		height_offset = height_offset - nRow;
	if (width_offset > 0.5*nCol)
		width_offset = width_offset - nCol;

	delete[] cross_real;
	cross_real = NULL;
}

文章收录：

这俩天一直在做关于物体匹配的方面的工作，前几天朋友推荐我看西安电子科技大学张瑞娟的一篇硕士论文“图像配准理论及算法研究”，我收获很大，所以我也总结一些对我有用的算法，将来便于查找应用。
我做的目标追踪这一块，虽然和图像配准不是一个方向，但是前期工作都是一样的，首先都需要物体检测，特征检测和匹配。这里我总结一些对我有用的，也希望对和我一样研究方向的人有帮助。这里图像配准可以换成物体匹配的。
1， 图像配准要素结合：特征空间，搜索空间，搜索策略，近似性度量
2， 图像配准方法：
2.1基于灰度信息的方法，
交叉相关（互相关）方法，相关系数度量，序贯相似检测算法，信息理论的交换信息相似性准则
2.2基于变换域的方法
相位相关法，Walsh Transform变换
2.3基于特征的方法
常用的图像特征有：特征点（包括角点、高曲率点等）、直线段、边缘（Robert、高斯-拉普拉斯LoG、Canny、Gabor滤波等边缘检测算子）或轮廓、闭合区域、特征结构以及统计特征如矩不变量等
注：像素灰度信息的互相关算法相比，特征提取包含了高层信号信息，所以该类算法对光照、噪声等的抗干扰能力强。
3，常用的空间变换模型
刚体变换（平移、旋转与缩放的组合）、仿射变换、透射变换、投影变换、非线性变换
4， 常用的相似性测度
4.1距离测度
均方根误差，差绝对值和误差，兰氏距离，Mahalanobis距离，绝对差，Hausdorff距离等
4.2角度度量法（概率测度）。
4.3 相关度量法
5，配准算法的评价标准
配准时间、配准率、算法复杂度、算法的可移植性、算法的适用性、图像数据对算法的影响等（这里虽然不是目标追踪的评价标准，但是我们可以借鉴这些评价算法的标准）

收录文章2：

cv::Point2d cv::phaseCorrelateRes(InputArray _src1, InputArray _src2, InputArray _window, double* response)  
{  
    //分别得到两幅输入图像和窗函数的矩阵形式  
    Mat src1 = _src1.getMat();  
    Mat src2 = _src2.getMat();  
    Mat window = _window.getMat();  
    //输入图像的类型和大小的判断，必须一致，而且类型必须是32位或64位浮点灰度图像  
    CV_Assert( src1.type() == src2.type());  
    CV_Assert( src1.type() == CV_32FC1 || src1.type() == CV_64FC1 );  
    CV_Assert( src1.size == src2.size);  
    //如果使用窗函数，则窗函数的大小和类型必须与输入图像的一致  
    if(!window.empty())  
    {  
        CV_Assert( src1.type() == window.type());  
        CV_Assert( src1.size == window.size);  
    }  
    //因为要进行离散傅立叶变换，所以为了提高效率，就要得到最佳的图像尺寸  
    int M = getOptimalDFTSize(src1.rows);  
    int N = getOptimalDFTSize(src1.cols);  
  
    Mat padded1, padded2, paddedWin;  
    //生成尺寸修改以后的矩阵  
    if(M != src1.rows || N != src1.cols)   //最佳尺寸不是原图像的尺寸  
    {  
        //通过补零的方式填充多出来的像素  
        copyMakeBorder(src1, padded1, 0, M - src1.rows, 0, N - src1.cols, BORDER_CONSTANT, Scalar::all(0));  
        copyMakeBorder(src2, padded2, 0, M - src2.rows, 0, N - src2.cols, BORDER_CONSTANT, Scalar::all(0));  
  
        if(!window.empty())  
        {  
            copyMakeBorder(window, paddedWin, 0, M - window.rows, 0, N - window.cols, BORDER_CONSTANT, Scalar::all(0));  
        }  
    }  
    else    //最佳尺寸与原图像的尺寸一致  
    {  
        padded1 = src1;  
        padded2 = src2;  
        paddedWin = window;  
    }  
  
    Mat FFT1, FFT2, P, Pm, C;  
  
    // perform window multiplication if available  
    //执行步骤1，两幅输入图像分别与窗函数逐点相乘  
    if(!paddedWin.empty())  
    {  
        // apply window to both images before proceeding...  
        multiply(paddedWin, padded1, padded1);  
        multiply(paddedWin, padded2, padded2);  
    }  
  
    // execute phase correlation equation  
    // Reference: http://en.wikipedia.org/wiki/Phase_correlation  
    //执行步骤2，分别对两幅图像取傅立叶变换  
    dft(padded1, FFT1, DFT_REAL_OUTPUT);  
    dft(padded2, FFT2, DFT_REAL_OUTPUT);  
    //执行步骤3  
    //计算互功率谱的分子部分，即公式3中的分子，其中P为输出结果，true表示的是对FF2取共轭，所以得到的结果为：P=FFT1×FFT2*，mulSpectrums函数为通用函数  
    mulSpectrums(FFT1, FFT2, P, 0, true);  
    //计算互功率谱的分母部分，即公式3中的分母，结果为：Pm=|P|，magSpectrums函数就是在phasecorr.cpp文件内给出的，它的作用是对复数取模。  
    magSpectrums(P, Pm);  
    //计算互功率谱，即公式3，结果为：C=P / Pm，divSpectrums函数也是在phasecorr.cpp文件内给出的，它仿照mulSpectrums函数的写法，其中参数false表示不取共轭  
    divSpectrums(P, Pm, C, 0, false); // FF* / |FF*| (phase correlation equation completed here...)  
    //执行步骤4，傅立叶逆变换  
    idft(C, C); // gives us the nice peak shift location...  
    /*平移处理，fftShift函数也是在phasecorr.cpp文件内给出的，它的作用是把图像平均分割成——左上、左下、右上、右下，把左上和右下对调，把右上和左下对调。它的目的是把能量调整到图像的中心，也就是图像的中心对应于两幅图像相频差为零的地方，即没有发生位移的地方。*/  
    fftShift(C); // shift the energy to the center of the frame.  
  
    //执行步骤5  
    // locate the highest peak  
    //找到最大点处的像素位置，minMaxLoc为通用函数  
    Point peakLoc;  
    minMaxLoc(C, NULL, NULL, NULL, &peakLoc);  
  
    // get the phase shift with sub-pixel accuracy, 5x5 window seems about right here...  
    //在5×5的窗体内确定亚像素精度的坐标位置  
    Point2d t;  
    // weightedCentroid也是在phasecorr.cpp文件内给出的，它是利用公式4来计算更精确的坐标位置  
    t = weightedCentroid(C, peakLoc, Size(5, 5), response);  
  
    // max response is M*N (not exactly, might be slightly larger due to rounding errors)  
    //求最大响应值  
    if(response)  
        *response /= M*N;  
  
    // adjust shift relative to image center...  
    //最终确定位移量  
    //先找到图像中点，然后用中点减去由步骤5得到的坐标位置  
    Point2d center((double)padded1.cols / 2.0, (double)padded1.rows / 2.0);  
  
    return (center - t);  
}  

参考资源：

【1】西北工业大学，吕海霞，硕士论文，《自动图像配准技术研究》，2007.3

【2】MIT,FFTW库

【3】Joseph L. Horner and Peter D. Gianino. Phase-only matched ltering. Applied Optics, 23(6):812-816, 1984.

【4】复旦大学，宋智礼，博士论文，《图像配准技术及其应用的研究》，2010,4

【5】中国科学技术大学信号统计处理研究院，郑志彬，叶中付，《基于相位相关的图像配准算法》，2006,12

【6】(美)冈萨雷斯著; 阮秋琦译. 数字图像处理(MATLAB 版) [M]. 北京：电子工业出版社, 2005.

【7】(美)冈萨雷斯著; 阮秋琦等译. 数字图像处理(第二版) [M]. 北京：电子工业出版社, 2003.

【8】感谢该博主对OpneCV相位相关库函数的解析，http://blog.csdn.net/zhaocj/article/details/50157801