四状态不可延展码的显式构造

具有显式恒定速率的四状态不可延展码

布瓦纳·卡努库尔蒂1(B)、赛·拉克什米·布瓦纳·奥巴图1(B)和斯鲁蒂·塞卡 尔2(B)
1印度科学研究所计算机科学与自动化系，印度班加罗尔bhavana@iisc.ac.in, oslbhavana@gmail.com2印度科学研究所数学系，印度班加罗尔 sruthi.sekar1@gmail.com

摘要

非延展性编码（NMCs），由兹杰姆博夫斯基、彼得扎克和维克斯 （ITCS2010）提出，通过提供一种强大的保障机制，推广了经典纠错码 的概念，即使在纠错码无法提供任何保障的场景下也能发挥作用：无论码 字中引入了多少错误，解码后的消息要么与原始消息相同，要么与原始消 息完全独立。非正式地说，非延展性编码是相对于一类篡改函数 F定义 的，其保证任何被篡改的码字只要使用函数 f ∈F进行篡改，解码后得到 的消息要么与原始消息相同，要么是一个独立的消息。

几乎所有已知的非延展性编码构造都是针对 t‐分状态家族，其中攻击 者任意但独立地篡改码字的每个 t “states”。切拉吉奇和古鲁斯瓦米（ TCC2014）在 t= O(n)的情况下获得了码率为1的非延展性编码，其中 n 为码字长度；并在（ITCS2014）中证明了对于任何 t‐分状态非延展性编 码，可达到的最佳速率的上界为 1 − 1/t。对于t= 10，查托帕迪亚和祖 克曼（FOCS2014）实现了一个恒定速率构造，但该常数未知。总之，目 前尚无任何t= o(n)情形下具有显式恒定速率的非延展性编码构造，更不 用说接近切拉吉奇和古鲁斯瓦米所给出的下界的构造了！

在这项工作中，我们构造了一种高效的非延展性编码，适用于 t‐分状 态模型，其中 t= 4，其码率达到常数 1 3+ζ ，对于任意常数 ζ> 0，且错 误率为 2 −Ω(/log c+1 )，其中 是消息长度， c> 0是一个常数。

1 引言

纠错码能够纠正数据中引入的错误。然而，由于它们只能纠正有限数量的错误， 其适用性受到限制。当数据被完全覆盖时，无法提供任何保护。 Dziembowski等人[15],提出的非延展性编码可保证：对数据造成的错误将使 其与原始消息无关，或保持不变。

非延展性编码由一组篡改函数族tampering函数F进行参数化，且仅当 m∗= Dec(f(Enc(m)))时（其中f ∈F，Enc,Dec分别为加密函数和解码函数）才保证非 延展性。（换句话说，当 f∈/F时没有保证。）直观上讲，给定一个篡改函数族F， 一个非延展性编码（Enc,Dec）将给定的消息 m编码成一个码字c ← Enc(m)，使 得如果 c被某个 f ∈ F修改为 c˜= f(c)，则在修改后的码字中解码得到的消息 m˜= Dec(c˜)要么是原始消息m，要么与 m“无关”且“独立”。

为了理解研究非延展性编码的动机，可以考虑其在密码学中的应用。在任 何标准的密码学安全游戏中，即使攻击者能够访问关于密钥的某些允许的输入‐ 输出行为，安全性通常也是有保障的 sk。1如果允许攻击者观察到关于某种修 改后 sk∗的输入‐输出行为，则我们不再能保证任何关于原始密钥 sk的安全性。 考虑一种情况：若不同于 sk∗的 sk被保证与 sk相互独立，则关于 sk∗的任何输 入‐输出行为都无法破坏关于 sk的安全性。（毕竟，如果获取一个独立的sk∗的 信息有助于破坏关于 sk的安全性，那么针对 sk的攻击者完全可以自行生成该 信息。）如果 sk使用非延展性编码进行编码，则非延展性将防止 sk∗取到任何 相关值，从而该方案仍能保持关于 sk的安全性。

毫不奇怪的是，自从被提出以来，非延展性编码已在许多领域找到了应用， 例如在抵御物理——泄露和篡改——攻击[15,21],、CCA安全加密的域扩展[8]以 及非延展性承诺[17]中。此外，非延展性编码激发了大量理论研究，这些研究 在非延展性提取器、加法组合学等主题之间建立了引人注目的联系。研究人员 一直对非延展性编码的两个方面非常感兴趣： （a）非延展性编码能够防范的篡改函数族的丰富程度，以及（b）码率（ = messagelength码字长度）他们所达到的。 我们的工作也属于这一领域，但特别关注码率。

1.1 相关工作

在[15], Dziembowski等人观察到，不可能构建相对于所有函数类安全的非延 展性编码。其背后的直觉是，该函数类将包含一个函数，该函数对加密函数(m) 进行解码，并将其重新编码为一个相关的值 m∗。此外，[15]证明了关于大小 小于 22 n的篡改函数族的非延展性编码的存在性结果。

一个自然但受限的篡改函数类别是按位篡改函数，其独立地修改码字的每 一位。Dziembowski等人[15]提出了针对该篡改族的非延展性编码构造。他 们的构造结合了线性纠错秘密共享方案（LECSS）2和代数操作检测码（ AMD码）3。在此之后，切拉吉奇和古鲁斯瓦米[7]给出了针对按位篡改族的最 优速率非延展性编码的显式构造。他们的构造结合了LECSS方案的性质、小消 息下的次优非延展性编码以及伪随机置换。

按位篡改族的一个自然推广是分状态篡改族，其中码字被分割成块（通常 是等长的，但并非必须如此），码字的每个块称为一个state，并被独立地篡改。 一个 t‐分状态族由作用于长度为 n/t的状态上的一组 t个函数组成，其中 n是 码字长度4。

在Dziembowski等人[15],的存在的结果基础上，Cheraghchi和 Guruswami表明，对于一个 t‐分状态族，每个码字状态包含 n/t比特时，可 达到的最佳速率的上界为1 −1/t。两者[6,15]都给出了2‐分状态模型下非延展 性编码的蒙特卡洛构造，证明了在随机预言模型中此类编码的存在性。[7]的工 作还在无种子t‐源非延展性提取器与 t‐分状态模型中的非延展性编码之间建立 了优雅的联系。

尽管在逐比特篡改函数族方面取得了进展，但分状态非延展性编码的首批 高效构造仍依赖于强假设，例如随机预言模型[15] 或处于计算环境[21]5中。 Dziembowski等人[14] 首次提出了分状态模型下非延展性编码的显式构造。 具体而言，他们使用内积提取器在2‐分状态模型中构造了针对1比特消息的非 延展性编码。在此基础上，阿加瓦尔等人[3] 提出了首个针对2‐分状态模型中 k‐比特消息的信息论构造，实现了码率Ω(n−6/7)。该构造依赖于内积

2 LECSS确保码字的比特位是 t‐wise独立的，并在码字被偏移量修改时检测篡改，当 Δ不是该方案的有效码字时。 Δ AMD编码检测向码字添加某个预定义偏移量 Δ的篡 改攻击。4 这类篡改函数族涵盖了其他篡改攻击，例如逐比特篡改、恒等 函数、常数函数等。研究此模型的一个动机来源于诸如云存储之类的实际应用，其中单 个文件可能被分割成 t多个部分并存储在 t不同的位置，而攻击者独立地篡改这些部 分中的每一个。因此，针对 t‐分裂状态族构造非延展性编码，且使 t> 1尽可能小，具 有理论和实际意义。5具体而言，刘和利西扬斯卡娅[21]在公共参考字符串（CRS）模 型中，基于数论假设并假设存在适用于适当NP语言的健壮的非交互式零知识证明系统， 提出了关于分裂状态篡改函数的计算型非延展性编码。

积函数，这是通过加法组合学的结果（包括拟多项式Freiman‐Ruzsa定理）得到的。

具有改进码率的非延展性编码：上述所有工作都集中在提高非延展性编码所能 容忍的篡改函数的丰富性上。然而，除了[7]针对按位篡改族的编码外，其余均 未实现最优速率。查托帕迪亚和祖克曼[5]首次在10‐分割状态模型中构造出了 高效常数速率非延展性编码。遗憾的是，他们所达到的码率是一个未知的常数， 在构建信息论原语时通常不理想。此外，正如在[2],中所观察到的，由于他们 使用了加法组合学，该码率可能是一个较小的（即较差的）常数。

对于2‐分状态模型，李在[20]中的构造实现了迄今为止已知的最佳码率， 即Ω(1/log n)。这两项工作都利用了无种子 t‐源非延展性提取器与 t‐分状态模 型中非延展性编码之间的联系，该联系源于[7]。阿加瓦尔等人[2]的研究给出了 各种分状态模型之间的优美关联。然而，由于李[20],指出的一个细微错误，他 们所提出的2‐分状态、常数速率非延展性编码的构造不再成立，这使得李的结 果成为2‐分状态模型中已知最佳的结果。不过，目前有两个被推测为常数速率 的NMC构造。具体而言，在[3],中，在内积猜想的前提下，作者得到了一个常 数速率的2‐分状态方案。此外，尽管[2],目前使用现有方法仅能实现线性速率 编码，但在适当的猜想下，它也能实现常数速率的2‐分状态编码。

我们从[6]中了解到关于可达到的最佳速率的以下内容：

引理1。 [6,第1节。1]。对于 t-分状态模型中的非延展性编码，且每个状态长 度相等时，可达到的最佳速率为 1 − 1 t。

尽管切拉吉等人在[7],中获得了针对 t= O（n）的速率1（最优）非延展性编码，但 对于 t= o（n），目前尚无达到最优码率1 − 1 t的构造方法，适用于 t‐分割状态模型。 在本研究中，我们在4‐分割状态模型中构造了一个码率为 1 3+ζ的非延展性编码，其中 ζ> 0为任意常数。

计算环境：如果我们借助计算假设，阿加瓦尔等人[1] 表明，可以构造出 具有最优码率且针对最不受限的t‐分割状态函数族的非延展性编码。具体而言， 他们获得了关于2‐分割状态篡改函数族的码率为1的计算型非延展性编码。不 幸的是，尽管付出了大量努力，目前已知最佳构造在计算环境与信息论环境下 的码率之间仍存在显著差距。

我们概述了Aggrawal等人在计算环境下提出的速率‐1构造[1]，并强调了 在信息论环境下构建此类代码所面临的挑战。他们的构造方法是选择一个密钥 kae用于计算认证加密方案，并使用低速率两分状态不可延展码对该密钥进行 编码，得到状态 c1, c2。该密钥用于计算待编码消息的认证加密密文(c3)，从而 得到一个三状态不可延展码：(c1, c2, c3)。（他们通过采用“增强型”非延展性 的一种扩展概念，得到了两分裂状态构造。）

代码。他们还证明了[3]的2状态构造实现了增强型非延展性。)码率最优性的关 键在于观察到，在计算环境中，用于认证加密的密钥长度可以很短（且独立于 消息长度）。

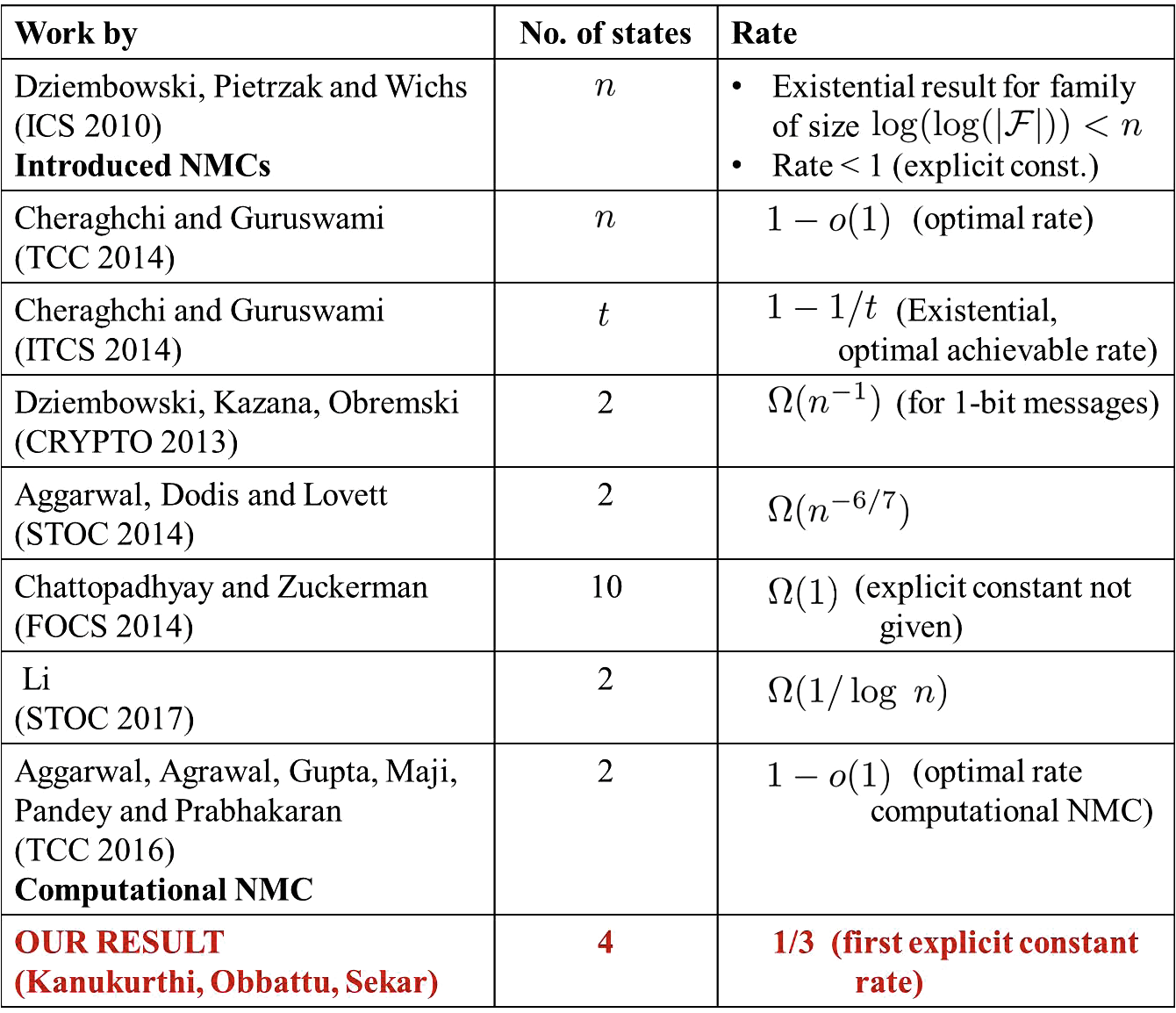
我们总结了关于 t‐分状态模型的非延展性编码的前期工作，见图1。

1.2 我们的结果

非正式地说，在本研究中，我们获得了在4‐分割状态模型下具有信息论常数码 率的非延展性编码。由于我们不依赖任何计算假设，这在构造和证明过程中带 来了一些独特的挑战，下面我们对此进行重点说明。作为起点，考虑上述描述 的相同构造[1]，但将其中的计算型认证加密方案替换为信息论意义上的加密 方案：我们仍然可以得到一个安全的非延展性编码。然而，对于一个信息论意 义上安全的加密方案，我们需要密钥的长度至少与消息长度相当。这意味着， 为了获得良好的码率，用作构建模块的分状态非延展性编码本身必须具有良好 的码率，因为它所编码的是

一个与消息m一样长的密钥ke——这正是我们试图解决的问题！

为了解决这一鸡与蛋问题，我们注意到认证加密方案可以模块化地分解为 一个认证方案和一个加密方案：即，首先使用通用的（一次性）加密方案对消 息进行加密，然后使用一次性消息认证码对其进行认证，从而构造出一个（一 次性）认证加密方案。好消息是，消息认证码仅需要较短的密钥（非正式地说， 长度与安全参数相当），因此可以使用非延展性编码对其进行编码，而不会影 响码率。这引出了以下方法：我们能否利用认证密钥的非延展性来对更大的消 息进行非延展性编码？

我们将通过讨论一些不正确的构造来说明我们构造的动机。考虑以下尝试： c1=(Encke(m),Tagka(Encke(m))); c2= ke;(c3, c4)= NMEnc(ka)，其中 Enc仅为一次性密码本加密，MAC=(Tag,Vrfy)为一次性消息认证码， NMEnc是一个两分裂状态非延展性编码，且{ci}i∈[4] 均存储在独立状态中。 该方案的一个根本问题是加密密钥未使用非延展性编码进行编码。攻击者只需 更改密钥 ke并保持其余编码部分不变，即可将被篡改的消息 m˜与原始消息 m 相关联。我们可以通过要求对加密密钥也进行认证来解决此问题。令 c1= (Encke(m),Tagka(Encke(m)||ke));c2=ke;(c3, c4)= NMEnc(ka)。虽然 ke的真 实性可能不再成问题，但这引入了另一个问题： c1包含在密钥 ke上计算的 MAC值，可能会泄露有关 ke的一些信息，因此密文c1可能不再安全。一次性 MAC的标准定义并不能保证原始消息的隐私性。（我们可以考虑同时保证隐私 性的特定MAC，但如上所述，我们需要的这类信息论安全的消息认证码无法使 用短密钥。）让我们尝试通过使用非延展性编码对标签进行编码来消除这种依 赖性。令c1=(Encke(m)); c2= ke;(c3, c4)= NMEnc(ka,Tagka(Encke(m)||ke))。 这导致了以下用于加密消息 m的候选构造： 1.为一次性密码本加密（Enc）选择一个密钥ke，并为一次性消息认证码（ MAC）选择一个密钥 ka。2.计算c1=Enc k e(m)，标签 t= Tagka(c1||ke)，并设 置 c2= ke。3.使用具有较低码率的两分裂状态非延展性编码，计算(c3, c4) ← NMEnc(ka, t)。4.输出c1, c2, c3, c4作为非延展性编码的四个状态。

直观上，这似乎是安全的，因为加密密钥 ke是经过认证的，并且其标签t是不 可篡改地编码的。因此，最理想的情况是，篡改函数˜ ˜只能使被篡改的 ka, t与底 层值相互独立。假设消息认证码在被篡改的密钥ke和标签t上验证通过，人们可能 会认为这保证了 ke的独立性，从而也保证了原始消息m m˜的独立性。然而，这种 推理对于具有短标签的MAC并不成立。具体而言，当标签远短于底层值时

消息m，对于给定密钥ke的标签空间中必然会出现碰撞——即，在同一个密钥 ke下，可能存在多个消息m映射到相同的标签值t。6正如我们在下面的攻击中 所描述的，这些“碰撞”可被利用来使代码变得“可延展的”。

对候选构造的攻击：为了描述一次攻击，我们需要指定篡改函数f1, f2, f3, f4。 在下面的描述中，我们使用 x[0] 表示二进制字符串 x 的最低有效位。

1.从加密密钥空间选择常数 k0, k1，从密文空间选择 ct0, ct1，使得 ct0[0]= k0[0]= 0, ct1[0]= k1[0]= 1 ，并选择一个标签 t∗和一个密钥 k∗ a， 使得Tagka∗(ct0||k0)= Tagka∗(ct0||k1)= Tagka∗(ct1||k0)= Tagka∗(ct1||k1)= t∗。 注意，这些值均独立于上述编码方案中的消息以及随机性。现在我们描述四个 篡改函数。2. f1(c1)：如果 c1[0]= 0，则设置 c1∗= ct0，否则 c1∗= ct1。3. f2(c2)：如果 c2[0]= 0，则设置 c2∗= k0，否则 c2∗= k1。4.计算 c3∗, c ∗ 4= NMEnc(k∗ a, t∗)。5. f3(c3)= c3∗。6. f4(c4)= c4∗。

仔细分析我们对各个常数的选择可知，被篡改的消息将保留原始消息的最 低有效位，即 m˜[0]= m[0]，其中 m˜是被篡改的消息。此外，攻击者利用了 MAC方案中的碰撞，以确保被篡改消息的标签和密钥始终能够通过验证。因此， 任何篡改行为都不会被检测到，并且会泄露关于原始消息的信息，从而违反非 延展性。

分析该攻击背后的直觉，我们发现主要挑战在于，即使密钥和密文是独立 被篡改的，它们联合起来仍可能保留关于原始消息的信息。为了克服这一问题， 我们修改了构造方法，以确保被篡改的密钥永远不会与原始密钥相关。实现这 种独立性成为我们的主要瓶颈。我们通过一种somewhatsurprising的方式 使用（强）随机性提取器，成功克服了这一瓶颈。

利用随机性提取器“放大”非延展性：非正式地说，随机性提取器允许我们 将非均匀随机性转化为均匀随机性。在这里，我们使用随机性提取器生成密钥 ke，即 ke= Ext(w; s)，其中 w和 s是适当长度的均匀随机字符串。一开始， 这看起来似乎完全毫无意义：毕竟，提取器通常用于无法获得完美随机性的情 况下。而此处显然并非如此：事实上，编码方案可以自行选择其随机性！如何 将 ke作为提取器的输出会带来任何

6此类问题不会出现在诸如 ax+ b的消息认证码中，其中(a, b)是MAC密钥， x是原始 消息。在此情况下，对于固定的密钥和固定的标签，存在唯一满足该线性方程的消息。

help?说明随机性提取器如何在此场景中发挥作用是我们的证明的关键。我们考虑 以下几种情况： 1. s, w均保持不变：在这种情况下，提取出的加密密钥保持不变。尽管目前 尚不清楚如何在此情形下论证非延展性，但暂时只需注意到上述描述的攻击已 不再相关，因此我们将其讨论留待后续。2. s被更改为一个独立的种子 s˜：7在 这种情况下， k˜e与 ke相互独立，无论 w˜如何依赖于 w。如前所述，此时上述 攻击也不再相关。˜3. s保持不变，但 w以相关方式被更改：在这种情况下， ke可能包含有关 ke的信息。

情况3似乎仍然保留了我们原来的瓶颈，我们通过确保在构造中，每当源 w发 生变化时，种子 s也必须随之改变来处理这一问题。这将其归约为情况2。剩 下的问题是如何通过巧妙地使用随机性提取器、消息认证码和非延展性编码来 实现这一点。

我们构造的概述：我们在构造中使用了以下工具：（a）一种针对2‐分状态 模型的非延展性编码，其实现的码率为 Ω(1/log n)[20]，其中 n 是块长度； （b）一种信息论安全的一次性消息认证码；（c）一种平均情况强随机性提取 器；（d）一种完全安全的加密方案，如一次一密。

步骤I：我们使用一个随机性提取器（通常具有短种子）来提取加密密钥。 步骤II：我们使用提取出的密钥对消息进行加密。 步骤III：为了检测用于提取密钥的源以及密文的修改，我们使用两个不同的一次性 MAC8对它们进行认证。 步骤IV：最后，我们使用两状态非延展性编码对认证密钥、标签以及用于 提取密钥的种子进行编码。我们输出双状态码字、源和密文。 步骤IV中的不可延展编码将我们构造的各个关键组件联系在一起，并在应对情况3 中描述的挑战时至关重要。

Proof Techniques:我们通过一系列统计上接近的混合体来证明非延展性，这些混 合体将我们从篡改游戏带入模拟游戏。但在我们的证明过程中出现了一些非平凡的 挑战：首先，各状态之间存在依赖性（例如：我们在一个状态中包含源，在另一个 状态中包含其标签的编码）。因此，即使各状态被独立修改，这些修改也会通过这 种依赖性相互关联。其次，尽管在我们的编码过程中我们是均匀随机地选择源，但 解码过程会揭示

7我们通过使用非延展性编码对 s进行加密来确保这一点。 8必须单独认证它们，因为 不对它们进行单独认证的构造是不安全的。这一点将在后续的安全证明中体现。

有关源的信息。这将阻止我们直接使用提取器安全性。在这里帮助我们的技巧 是，我们使用与种子无关的辅助信息来捕获通过解码获得的所有信息。独立于 种子。这将使我们能够在证明中使用关键的提取器安全性。

1.3 论文结构

我们在第节2和3中分别描述了构造的预备知识和构建模块。然后在第节4.2中给 出主要构造，接着在第节4.3中给出证明。随后在第节4.4、4.5、4.6和4.7中对 码率和错误进行了详细分析。

2 预备知识

符号说明。 κ表示安全参数。 s ∈R S表示从集合S中进行均匀采样。 x ← X 表示从概率分布X中采样。x||y表示两个二进制字符串 x和 y的连接。 |x| 表 示二进制字符串 x的长度。 Ul表示在{0, 1}l上的均匀分布。所有对数均为以2 为底的对数。

统计距离与熵。设X1, X2是某个集合 S上的两个概率分布。它们的统计距离为 SD(X1, X2) d=ef max T⊆S {Pr[X1 ∈ T] − Pr[X2 ∈ T]}= 1 2∑ s∈S ∣ ∣ ∣ ∣ Pr X1 [s] − Pr X2 [s] ∣ ∣ ∣ ∣ （如果SD(X1, X2) ≤ ε，则称它们为 ε‐接近，并记作 X1 ≈ε X2）。随机变量 W的最小熵定义为H∞(W)= −log(maxw Pr[W= w])。对于联合分布(W, E)， 定义在给定 E[12]的条件下 W的（平均）条件最小熵为 H˜∞(W | E)= −log(Ee←E(2−H∞(W|E=e))) （这里的期望是针对满足Pr[E= e]非零的 e取值）。对于定义在{0, 1}n上的 随机变量 W，若˜, t成立，则称 W|E为一个(n, t)‐源。

命题1。 设A1，…， An为互斥且穷尽的事件。则对于某个集合 S上的概率分布 X1、 X2，我们有： SD(X1, X2) ≤ n ∑ i=1 Pr[Ai].SD(X1|Ai, X2|Ai) 其中Xj|Ai是以事件 Ai为条件的 X j 的分布。

引理2. 对于任意随机变量 A, B, C，如果(A, B) ≈ε(A, C)，则 B ≈ε C。

引理3。 对于任意随机变量 A, B，如果A ≈ε B，则对任意函数f，f(A) ≈ε f(B)。

引理4。 设 A, B为定义在 A, B上的相关的随机变量。对于随机函数 F: A → X, G: A → X（所使用的随机性与 B独立），若 ∀ a ∈ A, F(a)≈ε G(a)，则(B, A, F(A)) ≈ε(B, A, G(A))

Proof. 2SD((B, A, F(A)),(B, A, G(A))) = ∑ b∈B,a∈A,x∈X ∣ ∣ ∣ Pr[B= b ∧ A= a ∧ F(A)= x] − Pr[B= b ∧ A= a ∧ G(A)= x] ∣ ∣ ∣ = ∑ b∈B,a∈A,x∈X Pr[B= b] ∣ ∣ ∣ Pr[A= a ∧ F(A)= x|B= b] − Pr[A= a ∧ G(A)= x|B= b] ∣ ∣ ∣ = ∑ b∈B,a∈A,x∈X Pr[B= b] Pr[A= a|B= b]. ∣ ∣ ∣ Pr[F(A)= x|A= a, B= b] − Pr[G(A)= x|A= a, B= b] ∣ ∣ ∣ = ∑ b ∈B ,a ∈A ,x ∈X Pr[B= b] Pr[A= a|B= b]. ∣ ∣ ∣ Pr[F(a)= x|B= b] − Pr[G(a)= x|B= b] ∣ ∣ ∣ = ∑ b ∈B ,a ∈A ,x ∈X Pr[B= b] Pr[A= a|B= b] ∣ ∣ ∣ Pr[F(a)= x] − Pr[G(a)= x] ∣ ∣ ∣ = ∑ b ∈B ,a ∈A Pr[A= a ∧ B= b]∑ x ∈ X ∣ ∣ ∣ Pr[F(a)= x] − Pr[G(a)= x] ∣ ∣ ∣ ≤ ∑ b ∈ B,a ∈A Pr[A= a ∧ B= b] · 2ε= 2ε

我们还使用以下引理[12,引理2.2b],该引理指出，随机变量的平均最小熵不 会减少超过相关随机变量的长度。

引理5。 如果 B至多有 2λ个可能的取值，则 ˜H∞(A | B) ≥H∞(A, B)− ˜ ˜λ ≥H∞(A) − λ。更一般地，H∞(A | B, C) ≥H∞(A, B | C) − λ ≥˜H∞(A | C) − λ。

2.1 定义

定义 1[7]。 一个（可能是随机的）函数Enc：{0, 1}l →{0, 1}n和一个确 定性函数Dec：{0, 1}n →{0, 1}l ∪{⊥}被称为一个编码方案，如果 ∀ m ∈{0, 1}l，Pr[Dec(Enc(m))= m]= 1。 l称为消息长度， n称为块 长度或码字长度。编码方案的码率为l。n

定义 2[7]。 一个编码方案(Enc,Dec)其消息空间和码字空间分别为{0, 1}l,{0, 1}n ，关 于函数族 F ⊆{f:{0, 1}n →{0, 1}n}是 ε -非可延展的，如果 对于 任意 ∀ f ∈ F, ∃存在一个分布 Simf在{0, 1}l ∪{same∗,⊥}上，使得 ∀ m ∈{0, 1}l Tampermf ≈ε Copy m Simf 其中Tampermf 表示分布解码函数(f(加密函数(m)))，而CopymSimf 的定义如下 m˜ ← Simf Copy m Sim f ={m if m˜= same∗ m˜ otherwise Simf在拥有对 f的预言机访问时应可被高效采样(.)。

3 构建模块

我们使用信息论消息认证码、强平均情况提取器以及李[20],提出的现有两分裂 状态非延展性码构造作为构建模块来构造我们的方案。下面我们简要讨论这些 构建模块。

3.1 一次性消息认证码

一组函数对 { {0, 1} γ × {0, 1} δ →{0, 1}}ka ∈ { 0,1 } τ k a {0, 1} γ →{0, 1} δ k a μ − Tag：，Vrfy：被称 为安全的一次性消息认证码，如果

1. For ka ∈R{0, 1} τ, ∀ m ∈{0, 1} γ, Pr[Vrfyka (m, Tagka (m))= 1]= 1.
2. For any m= m′, t, t′, Pr k a [Tagka (m)= t|Tagka (m′)= t′] ≤ μ for ka ∈R{0, 1} τ.

3.2 平均情况提取器

提取器[22]利用均匀随机种子 i作为一种催化剂，从具有高最小熵的随机变量中生 成接近均匀的字符串。强

提取器是指即使在已知种子的情况下，所提取的字符串看起来仍是随机的提取 器。（本文仅使用强提取器，因此有时会省略“强”这一形容词。）如果一个 提取器在对 W的保证是基于条件最小熵而非最小熵时仍然有效，则称之为平均 情况提取器。

定义 3[12,第2节5]。 设 Ext：{0, 1}n ×{0, 1}d →{0, 1}l是一个多项式时 间可计算函数。我们称Ext是一个高效的平均情况(n, t, d, l, ε)-强提取器，如果 对于所有满足˜W是一个 n比特字符串且H∞(W|I) ≥ t的随机变量对(W, I)， 都有SD((Ext(W; X) X, I),(U, X, I))，其中 X在{0, 1}d上均匀分布。

3.3 李的2‐分割状态非延展性编码构造

引理 6[20,定理7.12]. 对于任意 β ∈ N ，在具有块的二分状态模型中存在具有高效编解码器的 显式非可延展代码 长度 2β，码率 Ω( 1对数 β)和错误= 2 −Ω ⎛ ⎝ β 对数 β ⎞ ⎠。

设消息长度为 α引理中的非延展性编码6。根据引理6，我们有 α 2β=Ω( 1 log β) ⇒ α=Ω( β log(β)) 由引理10，我们有 β= O(α. log(α)) (1)

4 构造

在提出我们的构造之前，我们简要总结一下第1节中讨论的一些重要点。我们注 意到，如果消息 m在任何一个状态中以明文形式泄露，则该非延展性编码不太 可能是安全的。因为在这种情况下，该状态的篡改函数可以根据其获取的信息 决定是否进行篡改。正是由于这个原因，在我们的构造中，我们需要使用一次 一密对消息进行加密，然后将密钥和密文分别存储在独立状态中。为了防止攻 击者以相关的方式篡改这些信息，我们使用密钥 ka对其进行认证。我们将 ka 以及标签使用非延展性编码进行编码，以确保任何非平凡的篡改都会使它们与 底层的 ka和标签相互独立。然而，如第1节所述，如果我们以明文形式存储加密密钥 k，那么利用消息认证码中的碰撞，我们可以以相关的方式篡改密钥和 密文，从而导致产生相关的篡改消息。我们观察到，如果我们能够

˜将被篡改的密文关联起来，但不关联被篡改的加密密钥 k以 k，那么第1节中 描述的攻击不再成立。因此，我们在设计方案时需要解决的一个关键问题是：我们 能否确保任何被篡改的加密密钥˜与底层加密密钥 k 之间的独立性 k？ 我们展示了利用随机性提取器生成 k，并结合谨慎使用消息认证码，有助于实现这 种独立性。

4.1 符号说明

–NMEnc,NMDec是一个 ε1‐安全的双分割状态非延展性码，其消息空间和 码字空间分别为{0, 1}α、{0, 1}β1 ×{0
1}β2（如引理6所述），消息长度为 α，两个状态的长度分别为 β1、 β2。NMTamperfm1,f2 ,和NMSimf1,f2 分别表 示关于篡改函数 f1、 f2的被篡改的消息分布 m 以及NMEnc,NMDec的模 拟器。–Tag,Vrfy是一个信息论意义上ε2 ‐安全的一次性消息认证码（如引 理9所述），其密钥、消息、标签空间分别为{0, 1}τ1、{0, 1}n、{0, 1}δ1。– Tag′,Vrfy′ 是一个信息论意义上 ε3 ‐安全的一次性消息认证码（如引理9所述）， 其密钥、消息、标签空间分别为{0, 1}τ2、{0, 1}l、{0, 1}δ2。–Ext是一个(n, t, d, l, ε4)平均情况下的强提取器。 参数的选择将满足α= τ1+ τ2+ δ1+ δ2+ d和 n>1+ τ2+ δ2+ l+ t。（详见第 4.5节）

4.2 构造概述

我们现在定义一种用于四分割状态模型中 l位消息的构造方法。其思想是使用 随机性提取器（通常具有短种子）来提取密钥，然后使用底层非延展性码对种 子进行编码。此外，将源和密文存储在码字的不同部分。接着，我们使用两个 不同的一次性MAC方案对源和密文进行认证，然后使用底层非延展性码对认证 密钥和标签进行编码。换句话说，我们定义一个编码器，它输出密文、源（用 于提取加密密钥）以及对两对认证密钥和标签及种子进行编码的双状态码字。

构造方法如下所述：

加密函数(m) : – w ∈R{0, 1}n, s ∈R{0, 1}d– ka1 ∈R{0, 1} τ1, ka2 ∈R{0, 1} τ2– k= Ext(w, s)– C= m⊕ k– t1= 标签k a 1(w), t2=标签 ′ k a 2 (C)–(L, R) = NMEnc(ka1 ||ka2 ||t1||t2||s)–输出: (L, R, w, C)
加密函数(m) : – w ∈R{0, 1}n, s ∈R{0, 1}d– ka1 ∈R{0, 1} τ1, ka2 ∈R{0, 1} τ2– k= Ext(w, s)– C= m⊕ k– t1= 标签k a 1(w), t2=标签 ′ k a 2 (C)–(L, R) = NMEnc(ka1 ||ka2 ||t1||t2||s)–输出: (L, R, w, C)		解码函数(L, R, w, C): – ka1||ka2||t1||t2||s= NMDec(L, R) –如果 ka1||ka2||t1||t2||s= ⊥ 输出 ⊥–否则如果Vrfyka1(w, t1)= 1∧ Vrfy′ k a 2 (C, t2)= 1输出 C ⊕ Ext(w, s)–否则输出 ⊥
加密函数(m) : – w ∈R{0, 1}n, s ∈R{0, 1}d– ka1 ∈R{0, 1} τ1, ka2 ∈R{0, 1} τ2– k= Ext(w, s)– C= m⊕ k– t1= 标签k a 1(w), t2=标签 ′ k a 2 (C)–(L, R) = NMEnc(ka1 ||ka2 ||t1||t2||s)–输出: (L, R, w, C)

定理1。 设NMEnc、NMDec是一个 ε1-安全的双分割状态非延展性码，Tag、Vrfy 是一个信息论 ε2安全的一次性MAC ，且Tag′,Vrfy′是如上所述的一个信息论 ε3 安全的一次性MAC。设Ext是一个(n, t, d, l, ε4)平均情况下的强提取器。令 α= τ1+ τ2+ δ1+δ2+ d且 n> 1+ τ2+ δ2+ l+ t。 对于任意常数 ζ> 0，长度为 l的消息，以及满足 κ 的任意 κ= o( l log l)，上图中的构造是一个非延展性编码，其块长度为(3+ ζ)l+ o(l)，从而实现 渐近码率 1 3+ ζ 和错误 2−κ。

证明。 我们分两步给出证明。首先，我们证明所提出的构造是一个非可延展的 编码方案（第4.3节）。其次，我们设置参数以达到期望的码率和错误（第4.4节）。

4.3 安全性证明

为上述构造定义四分割态篡改族 F={(h1, h2, f, g): h1:{0, 1}β1 →{0, 1}β1, h2:{0, 1}β2 →{0, 1}β2, f:{0, 1}n →{0, 1}n, g:{0, 1}l →{0, 1}l} 为了证明（加密函数,解码函数）是不可延展的，我们需要证明 ∀(h1, h2, f, g) ∈F, ∃ Simh1,h2,f,g使得 ∀ m ∈{0, 1}l T amper m h1,h2,f,g ≈ε Copy m Simh1,h2,f,g 设(h1, h2, f, g) ∈F。我们定义以下模拟器： Simh1,h2,f,g：1. k ∈R{0, 1}l2. C= 0 ⊕ k3. w ∈R{0, 1}n ˜ 4.( w˜, C)=(f(w) g(C))5. k˜a1|| k˜a2|| t˜1|| 6 ⊥ 7 。如果 k˜a1|| k˜a2|| t˜1|| t˜2||s˜= ⊥，输出。否则如果 k˜a1|| k˜a2|| t˜1|| t˜2||s˜= same∗ ˜ a.如果 w˜= w 且 C= C，输出 same∗b.否则输出 ⊥8.否则如果验证 ˜ k 1( w˜, t˜1)= 1 ∧验证 ′ ˜ k a 2 ( C˜, t˜2)= 1，输出Ext(w ˜; s˜)9.否则输出 ⊥

我们现在通过一系列混合体来证明篡改的随机变量与模拟的随机变量之间的统计接 近性。

证明概述。 从高层来看，我们的目标是通过一系列混合体来消除 m˜对 m的依赖 性。码字通过各种随机变量（例如种子 s、 w、认证密钥以及标签）直接或间接 地依赖于 m。首先，我们希望消除用于解密码字的篡改的提取密钥对原始提取 密钥的依赖性。通过一系列混合体，我们通过消除篡改的提取密钥对种子 s的依 赖性来实现这一点。一旦完成此操作，我们将利用提取器的性质，以消除 C对 w和 s的依赖性。最后，我们利用一次一密的完美˜安全性来消除 C对 m的依 赖性。

从篡改实验到混合体1mh1,h2,f,g: 混合体1mh1,h2,f,g与标准篡改实验相同，只是 我们使用底层非延展性编码的模拟器来生成篡改的随机变量 k˜a1|| k˜a2|| t˜1|| t˜2||s˜。

声明。 如果(NMEnc,NMDec)是一个ε1安全的非延展性编码，则Tampermh1, h2,f,g ≈ε1 Hybrid1 m h1,h2,f,g

		混合1mh1,h2,f,g： 1. w ∈R{0, 1}n, s ∈R{0, 1}d 2. k1a ∈R{0, 1}τ1, ka 2 ∈R{0, 1}τ2 3. k= Ext(w; s) 4. C= m⊕ k 5. t1=标签 ka1 (w), t2=标签 ′ ka2(C) 6.(w ˜, C˜)=(f(w) g(C)) 7a. k˜a1|| k˜a2|| t˜1|| t˜2||s˜ ← NMSimh 1,h2 7b. If k˜a1|| k˜a2|| t˜1|| t˜2||s˜= same∗, 分配 k˜a1|| k˜a2|| t˜1|| t˜2||s˜ = ka1||ka2||t1||t2||s 8. If k˜a1|| k˜a2|| t˜1|| t˜2||s˜= ⊥，输出 ⊥ 9.否则 if Vrfy ˜ k a 1 ( w˜,t ˜1)= 1 ∧ Vrfy ′ ˜ k a 2 (C ˜, t˜2)= 1 四态不可延展编码及 其显式常数速率 C˜ ⊕ Ext(w ˜; s˜)
篡改m h1,h2,f,g: 1. w ∈R{0, 1}n, s ∈R{0, 1} d 2. ka1 ∈R{0, 1}τ1, ka 2 ∈R{0, 1}τ2 3. k= Ext(w; s) 4. C= m⊕ k 5. t1=Tag ka1 (w), t2=标签 ′ ka2(C) 6.(w ˜, C˜)=(f(w) g(C)) 7. k˜a1|| k˜a2|| t˜1|| t˜2||s˜ ← NMTamper ka1||ka2||t1||t2||s h1,h2 8. If k˜a1|| k˜a2|| t˜1|| t˜2||s˜= ⊥,output ⊥ 9.否则 if验证 ˜ k a 1 ( w˜,t ˜1)= 1 ∧ Vrfy′ ˜ k a 2 (C ˜, t˜2)= 1 输出 C˜ ⊕ Ext(w ˜; s˜) 10.否则输出 ⊥		混合1mh1,h2,f,g： 1. w ∈R{0, 1}n, s ∈R{0, 1}d 2. k1a ∈R{0, 1}τ1, ka 2 ∈R{0, 1}τ2 3. k= Ext(w; s) 4. C= m⊕ k 5. t1=标签 ka1 (w), t2=标签 ′ ka2(C) 6.(w ˜, C˜)=(f(w) g(C)) 7a. k˜a1|| k˜a2|| t˜1|| t˜2||s˜ ← NMSimh 1,h2 7b. If k˜a1|| k˜a2|| t˜1|| t˜2||s˜= same∗, 分配 k˜a1|| k˜a2|| t˜1|| t˜2||s˜ = ka1||ka2||t1||t2||s 8. If k˜a1|| k˜a2|| t˜1|| t˜2||s˜= ⊥，输出 ⊥ 9.否则 if Vrfy ˜ k a 1 ( w˜,t ˜1)= 1 ∧ Vrfy ′ ˜ k a 2 (C ˜, t˜2)= 1 四态不可延展编码及 其显式常数速率 C˜ ⊕ Ext(w ˜; s˜)
10.否则输出 ⊥

证明。 我们希望利用与（NMEnc,NMDec）相关的被篡改的随机变量和模拟的随 机变量之间的统计接近性，来证明该声明。 现在，我们应用引理4，取 B=(w, C) A=(ka1||ka2||t1||t2||s)，并将函数设为 NMTamperh1,h2,CopyNMSimh1 ,h2，得到： Since, NMTamperka1||ka2||t1||t2||s h1,h2 ≈ε1 Copy ka1||ka2||t1||t2||s NMSimh1,h2 因此我们得到， (w, C, ka1||ka2||t1||t2||s, NMTamperka1||ka2||t1||t2||s h1,h2 ) ≈ε1 (w, C, ka1||ka2||t1||t2||s, Copy ka1||ka2||t1||t2||s NMSimh1,h2 ) 由引理2，(w, C, NMTamperka1||ka2||t1||t2||s h1 h2 ,) ≈ε1(w, C, Copyka1||ka2||t1||t2||s NMSimh1,h2) =⇒ By Lemma 3,(w ˜, C˜, NMTamperka1||ka2||t1||t2||s h1,h2 ) ≈ε1(w ˜, C˜, Copy ka1||ka2||t1||t2||s NMSimh1,h2) (2) 现在，我们将混合体的输出表示为上述变量的确定性函数Q，以应用引理3，从而证明该 声明。和因此证明该声明。 Q( w˜, C˜, k˜a1|| k˜a2|| t˜1|| t˜2||s˜)： – If k˜a1|| k˜a2|| t˜1|| t˜2||s˜= ⊥, output ⊥ – else if Vrfy ˜ ka1(w ˜, t˜1)= 1 ∧ Vrfy′ ˜ – else output ⊥ 然后，利用公式2和引理3，我们得到 Q(w ˜, C˜, NMTamper ka1||ka2||t1||t2||s h1,h2 ) ≈ε1 Q(w ˜, C˜, Copy ka1||ka2||t1||t2||s NMSimh1,h2 ) =⇒ Tampermh1,h2,f,g ≈ε1 Hybrid1mh1,h2,f,g

从混合实验Hybrid1mh1,h2,f,g到Hybrid2mh1,h2,f,g： 正如稍后将变得明显的 那样，Hybrid1mh1,h2,f,g将使我们能够论证，在˜ s˜= s的受限情况下，提取的密 钥 k与 s相互独立。现在我们转向Hybrid2mh1,h2,f,g，它与Hybrid1mh1,h2,f,g相 同，除了 s保持不变的情况。在这种情况下，正如我们在Hybrid2mh1,h2,f,g中所 展示的，实验的输出可以在不计算˜的情况下得出。我们通过利用消息认证方案 的不可伪造性来证明Hybrid1mh1,h2,f,g和Hybrid2mh1,h2,f,g在统计上接近。

声明。 如果（Tag,Vrfy）和（Tag′,Vrfy′）分别是 ε2‐、 ε3‐安全的信息论 一次性MAC（分别），则Hybrid1 m h 1 ,h 2 ,f,g ≈ε 2 +ε 3 Hybrid2 m h 1 ,h 2 ,f,g。

Hybrid1mh1,h2,f,g:

1. w ∈R{0, 1}n, s ∈R{0, 1}d 2. ka1 ∈R{0, 1}τ1, ka2 ∈R{0, 1}τ2 3. k= Ext(w; s)4. C= m⊕ k5. t1=标签ka1(w), t2=标签′ka2(C)˜ 6.( w˜, C)=(f(w) g(C))7. k˜a1|| k˜a2|| t˜1|| t˜2||s˜ ←NMSimh1,h28. 如果 k˜a1|| k˜a2|| t˜1|| t˜2||s˜= same∗，分 配 k˜a1|| k˜a2|| t˜1|| t˜2||s˜ = ka1||ka2||t1||t2||s9.如果 k˜a1|| k˜a2|| t˜1|| t˜2||s˜= ⊥，输出⊥10. 否则如果验证 ˜ ka1( w˜, t˜1)= 1 ∧验 证′ ˜ ka2( C˜, t˜2)= 1˜输出 C ⊕ Ext(w ˜; s˜) 11.否则输出 ⊥
1. w ∈R{0, 1}n, s ∈R{0, 1}d 2. ka1 ∈R{0, 1}τ1, ka2 ∈R{0, 1}τ2 3. k= Ext(w; s)4. C= m⊕ k5. t1=标签ka1(w), t2=标签′ka2(C)˜ 6.( w˜, C)=(f(w) g(C))7. k˜a1|| k˜a2|| t˜1|| t˜2||s˜ ←NMSimh1,h28. 如果 k˜a1|| k˜a2|| t˜1|| t˜2||s˜= same∗，分 配 k˜a1|| k˜a2|| t˜1|| t˜2||s˜ = ka1||ka2||t1||t2||s9.如果 k˜a1|| k˜a2|| t˜1|| t˜2||s˜= ⊥，输出⊥10. 否则如果验证 ˜ ka1( w˜, t˜1)= 1 ∧验 证′ ˜ ka2( C˜, t˜2)= 1˜输出 C ⊕ Ext(w ˜; s˜) 11.否则输出 ⊥		Hybrid2mh1,h2,f,g：1. w ∈R{0, 1}n, s ∈R{0, 1}d3. k= Ext(w; s)4. C= m⊕ k˜6. ( w˜, C)=(f(w) g(C))7. k˜a1|| k˜a2|| t˜1|| t˜2||s˜ ←NMSimh1,h2 8.如果 k˜a1|| k˜a2|| t˜1|| t˜2||s˜= same∗ ˜ 如果 w˜= w且 C= C输出m •否则输出 ⊥9.如果 k˜a1|| k˜a2|| t˜1|| t˜2||s˜= ⊥，输出⊥10. 否则如果验证 ˜ ka1( w˜, t˜1)= 1 ∧验 证′ ˜ ka2( C˜, t˜2)= 1˜输出 C ⊕ Ext(w ˜; s˜) 11.否则输出 ⊥

证明。 如果 same∗不是从NMSimh1,h2中采样的值，则Hybrid1mh1,h2,f,g和 Hybrid2mh1,h2,f,g可以分别在不执行步骤(2,5,8)和步骤(8)的情况下进行评估。 在此情况下，这两个混合体的输出完全相同。因此，此时统计距离为零。当 same∗被采样时，Hybrid1mh1,h2,f,g与Hybrid2mh1,h2,f,g之间的关键区别在于， 针对此情况，我们在Hybrid2mh1,h2,f,g中移除了步骤10中的两个验证检查，并 简单地将其替换为步骤8中所示的检查。根据命题1以及上述观察，我们得到： SD(Hybrid1 m h1,h2,f,g ; Hybrid2 m h1,h2,f,g) ≤ Pr[NMSimh1,h2= same ∗ ] · SD(Hybrid1 m h 1 ,h 2,f,g |NMSimh1, h2= same ∗;Hybrid2 m h 1 ,h 2,f,g |NMSimh1, h2= same ∗ ) 因此，现在只剩下NMSimh1,h2输出 same∗的情况。通过利用(Tag,Vrfy)和 (Tag′,Vrfy′)的不可伪造性，我们证明了这两个混合体在统计上是接近的。 ˜–设事件E为 same∗从NMSimh1，h2中采样的事件，其补事件为 E。 ˜ ˜–设事件F为 w˜= w ∧ C= C的事件，其补事件为 F。˜–事件E 与 F相互独立，因为 w˜， C分别是 w和 C的确定性函数（而 w和 C与 NMSimh1， h2无关），且NMSimh1， h2除了预先固定的篡改函数 h1， h2外 不接受任何输入。

2SD(Hybrid1mh1,h2,f,g; Hybrid2mh1,h2,f,g) = ∑ m˜∈{0,1}l∪{⊥} ∣∣∣Pr[Hybrid1mh1,h2,f,g= m˜] − Pr[Hybrid2mh1,h2,f,g= m˜] ∣∣∣ = ∑ m˜∈{0,1}l∪{⊥} ∣∣∣Pr E + Pr E ˜ ︸ ︷︷ ︸ =0 as given E˜ both the hybrids are identical. ∣∣∣ = ∑ m˜∈{0,1}l∪{⊥} Pr[E] ∣∣∣ Pr[Hybrid1mh1,h2,f,g= m˜|E] − Pr[Hybrid2mh1,h2,f,g= m˜|E] ∣∣∣ = Pr[E] ∑ m˜∈{0,1}l∪{⊥} ∣ ∣ ∣ Pr[F|E]. ( Pr[Hybrid1mh1,h2,f,g= m˜|E, F] − Pr[Hybrid2mh1,h2,f,g= m˜|E, F] ︸ ︷︷ ︸ =0 as given E and F both the hybrids outputm.So for any m˜ the difference is 0 )+ Pr[F ˜|E]. (Pr[Hybrid1mh1,h2,f,g= m˜|E, F˜] − Pr[Hybrid2mh1,h2,f,g= m˜|E, F˜])∣ ∣ = Pr[E] ∑ m˜∈{0,1}l ∪{⊥} ∣ ∣ ∣ Pr F ˜ ∣ ∣ = Pr[E] Pr[F ˜] ∑ m˜∈{0,1}l ∣ ∣ ∣ Pr[Hybrid1mh1,h2,f,g = m˜|E, F˜] − Pr[Hybrid2mh1,h2,f,g = m˜|E, F˜] ∣∣∣ + ∣ ∣ Pr[Hybrid1mh1,h2,f,g = ⊥|E, F˜] − Pr[Hybrid2mh1,h2,f,g = ⊥|E, F˜] ︸ ︷︷ ︸ = 1 as given E, F˜ Hybrid 2 outputs ⊥ ∣ ∣ ∣ = Pr[E] Pr[F ˜] ∑ m˜∈{0,1} l Pr[Hybrid1mh1,h2,f,g = m˜|E, F˜]+1 − Pr[Hybrid1mh1,h2,f,g = ⊥|E, F˜] = 2 Pr[E] Pr F ˜ ≤ 2 Pr[E] Pr[F ˜] Pr[Vrfy ˜ k a 1 (w ˜, t˜1)= 1 ∧ Vrfy ′ ˜ k a 2 (C ˜, t˜2)= 1|t1= Tagka1 (w), t2= Tag ′ k a 2 (C), E, F˜] ≤ 2 Pr[E] Pr[F ˜] Pr[Vrfyka1 (w ˜, t1)= 1 ∧ Vrfy ′ k a 2 (C ˜, t2)= 1|t1= Tagka1 (w), t2= Tag ′ k a 2 (C), F˜] ≤ 2(ε2+ ε3) ∴ Hybrid1 m h 1 ,h 2 ,f,g ≈ε 2 +ε 3 Hybrid2 m h 1 ,h 2 ,f,g

重写Hybrid2mh1,h2,f,g为Hybrid3mh1,h2,f,g： 现在我们只需重写Hybrid2mh1,h2,f,g，从 NMSimh1,h2开始采样。

Hybrid2mh1,h2,f,g:

1. w ∈R{0, 1}n, s ∈R{0, 1}d 2. k= Ext(w; s) 3. C= m⊕ k 4.(w ˜, C˜)=(f(w) g(C)) 5. k˜a1|| k˜a2|| t˜1|| t˜2||s˜ ← NMSimh1,h2 6. If k˜a1|| k˜a2|| t˜1|| t˜2||s˜= same∗ •如果 w˜= w并且 C˜= C输出m •否则输出 ⊥ 7. If k˜a1|| k˜a2|| t˜1|| t˜2||s˜= ⊥，输出 ⊥ 8.否则 if验证 ˜ k a1( w˜,t ˜1) = 1 ∧ 验证′ ˜ k 输出 C˜ ⊕ Ext(w ˜; s˜) 9.否则输出 ⊥		1. k˜a1|| k˜a2|| t˜1|| t˜2||s˜ ← NMSimh1,h 2 2. w ∈R{0, 1}n, s ∈R{0, 1}d 3. k= Ext(w; s) 4. C= m⊕ k 5.(w ˜, C˜)=(f(w) g(C)) 6. If k˜a1|| k˜a2|| t˜1|| t˜2||s˜= same∗ •如果 w˜= w且 C˜= C输出m •否则输出 ⊥ 7. If k˜a1|| k˜a2|| t˜1|| t˜2||s˜= ⊥，输出 ⊥ 8.否则 if验证 ˜ k a1( w˜,t ˜1) = 1 ∧ 验证′ ˜ k 四态非延展性编码具 有显式恒定速率 C˜ ⊕ Ext(w ˜; s˜) 9.否则输出 ⊥
Hybrid3mh1,h2,f,g:

很容易看出，我们在不改变任何随机变量分布的情况下重新排列了步骤， Hybrid2mh1,h2,f,g ≡Hybrid3mh1,h2,f,g。

从Hybrid3mh1,h2,f,g到Hybrid4mh1,h2,f,g： 我们现在希望消除密文对源的依 赖性。这将消除包含 w和 C的两个状态之间的依赖性，这种依赖性可能导致消 息的相关篡改。为此，我们希望利用随机性提取器的安全性，并将提取的密钥 k替换为均匀分布的密钥。这样做的主要挑战在于，解码后的（被篡改的）消 息本身可能会泄露关于密钥 k的信息。这是一个挑战，因为这些信息是在种子 s 选择之后才被获取的。这是我们证明中的主要瓶颈。我们克服这一问题的方法 是仔细论证由解码消息所泄露的信息可能从辅助信息中获得。重要的是，该辅 助信息与 s完全独立，因此我们可以使用提取器安全性。

声明。 如果Ext是(n, t, d, l, ε4)平均情况提取器，则Hybrid3 m h1,h2,f,g ≈ε4Hybrid 4 m h1,h2,f,g

Hybrid3mh1,h2,f,g： 1. k˜a1|| k˜a2|| t˜1|| t˜2||s˜ ← NMSimh 1,h2 2. w ∈R{0, 1}n,s ∈R{0, 1}d 3. k= Ext(w; s) 4. C= m⊕ k 5.(w ˜, C˜)=(f(w) g(C)) 6. If k˜a1|| k˜a2|| t˜1|| t˜2||s˜= same∗ •如果 w˜= w并且 C˜= C输出m 否则输出 ⊥ 7.否则如果 k˜a1|| k˜a2|| t˜1|| t˜2||s˜= ⊥，输出‐ 输出 ⊥ 8.否则 if验证 ˜ k a1( w˜,t ˜1) = 1 ∧ 验证′ ˜ ka2(C ˜, t˜2)= 1 四态不可延展码具有 显式常数速率 C˜ ⊕ Ext(w ˜; s˜) 9.否则输出 ⊥		Hybrid4mh1,h2,f,g： 1. k˜a1|| k˜a2|| t˜1|| t˜2||s˜ ← NMSimh 1,h2 2. w ∈R{0, 1}n 3. k ∈R{0, 1}l 4. C= m⊕ k 5.(w ˜, C˜)=(f(w) g(C)) 6. If k˜a1|| k˜a2|| t˜1|| t˜2||s˜= same∗ •如果 w˜= w并且 C˜= C输出m •否则输出 ⊥ 7.否则如果 k˜a1|| k˜a2|| t˜1|| t˜2||s˜= ⊥，输‐ 出 ⊥ 8.否则 if验证 ˜ k a1( w˜,t ˜1) = 1 ∧ 验证′ ˜ ka2(C ˜, t˜2)= 1 输出 E˜xt(w ˜; s˜) 9.否则输出 ⊥

证明。 正如本声明的动机所述，我们希望用一个均匀的字符串替换提取器输出。 但其中的主要挑战在于，在给定辅助信息的情况下如何保证安全性。我们考虑 两种情况，并仔细分析每种情况下所使用的