k近邻法 kd树 平衡kd树

k近邻法

k近邻法的思想：

k近邻法是一种基本分类与回归方法。输入为实例的特征向量，输出为实例的类别（可取多类）。具体过程是：给定一个已经分好类的数据集，对于新的实例，加入此数据集，以离这个点最近（距离度量）的k个点（k值选取）的类别进行多数表决（分类策略）去决定这个新的实例的类别。

k近邻法三要素：

k值的选择：

k小，用于训练的点少，只有新实例点旁边的点起作用（表决），近似误差小，估计误差大；k大，用于训练的点的数量多，模型较简单，近似误差大，估计误差小。

距离的度量：

特征空间中两个实例之间的距离是两个实例之间相似程度的度量。距离的度量方式有L1距离(曼哈顿距离)L2距离（欧式距离）,更一般的Lp距离或明氏距离。

分类的策略：

多数表决。等价于经验风险最小化。

kd树

kd树是什么：

k近邻法需要判断实例点之间的距离，大规模数据时，不停的计算距离显然是一件十分耗时的事情。为了减少计算的次数以提高效率，考虑用特殊的结构去存储训练数据，这里用kd树来存储。kd树首先是一种二叉树。因为数据可以是高维的，所以对应的kd树的每个节点都是一个k维数值点的二叉树。这也是与以前学的二叉树的一个不同。kd树主要应用在高维数据索引上，做空间划分和近邻搜索。以上是kd树的作用，明白了它是用来划分高维空间、存储高维数据的之后，接下来要知道kd树如何构造，怎么就划分了高维空间了，以及怎么样搜索就减少了计算的次数了。

kd树的构造

一维数据构造的二叉树及其查找过程：

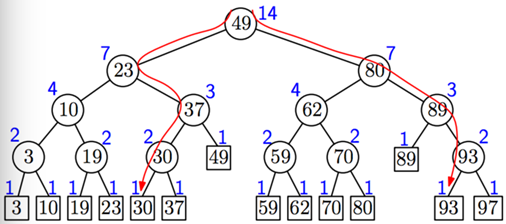
比如这是一个班里语文的成绩，现在想找出来成绩在区间[40,80]之间的，很好找，设此集合为S1。