密码学相关

一、加解密算法

1、对称加密

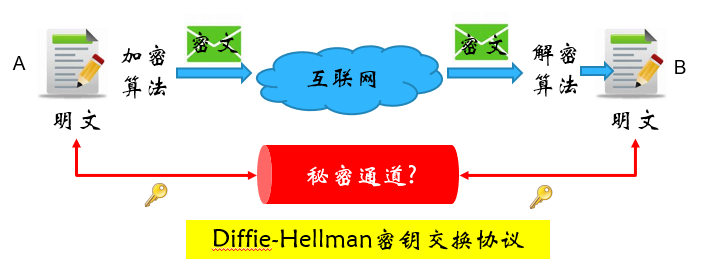
对称加密模型中，加密解密使用同一个密钥，密钥的首次传送需用秘密通道，类别有流密码和分组密码。

 1.流密码

• 一次一密，逐比特加密
• 仅用于在传递机密参数时进行加密

例：RC4:秘钥调度算法+伪随机密码生成算法

2、分组密码

2.1 DES算法

• 分组长度64位，密钥长度64位（其中仅56位有效）
• 
• 1998年以后逐渐由于容易被破解被替代

 

2.2 3-DES算法

• 在DES的基础上用3个密钥对明文加密三次
• 缺点：慢了、

2.3 IDES算法

• 密钥长度128位，分组长度64位

2.4 AES算法

• 分组长度128位，密钥长度128/192/256位

二、非对称加密（ 公开密钥）

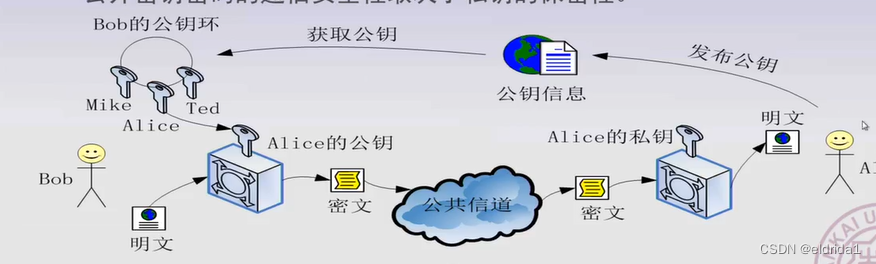
• 公开密钥密码的通信安全性取决于私钥的保密性，公钥可以经过互联网传输        VS        对称加密算法：取决于密钥的保密性 ，密钥传输需经过秘密通道
• 核心思想：           单项陷门函数f（x）

1、公开密钥的应用——认证模型 

 

 Q：如何保证公钥的真实性？

A:证书

2、公钥密码算法

2.1、Diffie-Hellman密钥交换算法

• 只能用来交换密钥，不能用来加密信息
• 可以为对称加密算法交换密钥，建立有关安全的传输通道

原理：

• 原根：如果a是素数p的原根，则对于任意的整数b，一定能找到唯一的幂i（1=<i<=p-1)，使得,且可以证明素数一定存在原根。

      如素数7的原根3

•   离散对数：若a是素数p的一个原根，则对于任意整数b，一定能找到唯一的幂i（1=<i<=p-1)，使得,i称为b的以a为基数且模p的幂指数，即离散对数。对于函数,已知g,x,p，计算y是容易的；而已知y,g,p，计算x是困难的。
• Diffie-Hellman密钥交换算法：1）Alice和Bob协商好原根大素数p，和大的整数g，其中g是p的原根，p跟g无需保密。

  

2.2、RSA公开密钥算法 

(1)原理：

• 大整数因子分解问题：已知p，q为两个大素数，则求N=pxq是容易的，只需要一次乘法运算；但已知N是两个大素数的乘积，要求将N分解是很困难的。
• 欧拉定理及其推论：给定两个素数p和q，以及两个整数m、n，使得n=pxq，且0<m<n,则对于任何整数，
• RSA密码算法：

  参数	解释	公式	描述
  P、Q	质数	P*Q=N	分解模数N后得到的值
  N	公共模数	N=P*Q	在RAS中进行模运算
  e	公钥指数	gcd(φ,e)=1	1<e<φ,与φ互素
  d	私钥指数	gcd(φ,d)=1	1<d<φ，且为模φ下e的乘法逆元，即（d * e） mod φ=1
  φ	欧拉公式	φ=(P-1)*(Q-1)	/
  c	密文	c=m^e mod N	/
  d	明文	m=c^d mod N	/

 公钥Pk={e,n},私钥Sk={d，n，p，q}

加密算法：c=m^e mod N

解密算法：m=c^d mod N

原因：m=c^d mod N=m^(e*d) mod N=m^(k*φ+1) mod N=m mod N=m

二、散列函数

1、散列函数的目的

将任意长的消息映射成一个固定长度的hash值，也成为消息摘要。消息摘要可以作为认证符，完成消息认证。

2、散列函数的健壮性

• 强无碰撞性：两个不同的变量一定对应两个不同的hash函数值
• 单向性：由自变量求函数值容易，由函数值反求自变量很难
• 散列函数可将任意长度的比特串映射到一个定长的比特串(摘要，指纹)
• 散列值的安全长度不低于128位（“生日悖论”）

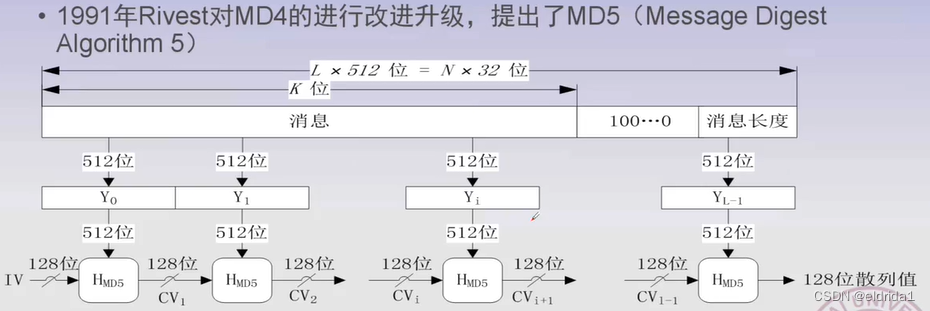
3、MD5

对于任意明文生成128位散列值

三、相关应用

 1、消息认证

1.1 概述

目的：1）证明消息的信源和信宿的真实性；2）检验消息内容是否曾受到偶然或有意的篡改；

3）消息的序号和时间性是否正确。

1.2 主要方式

消息认证由具有认证功能的函数来实现的，主要方式有：

• 用消息的完整密文作为消息的认证符
• 消息认证码MAC，也称密码校验和，使用密码对消息加密，生成固定长度的认证符
• 消息编码，是针对信源消息的编码函数，使用编码抵抗针对消息的攻击

1.3 消息加密函数

既可以用公钥函数，也可以用私钥函数

• 对称密钥密码对消息加密，不仅具有机密性，同时具有一定的可认证性。
• 公开密钥密码本身就提供认证功能

 1.4 消息认证码MAC

基本思想：

• 发送方利用事先约定的密码，加密生成一个固定长度的短数据块MAC，并将MAC附加在消息之后，一起发送给接收者
• 接收方使用相同密码对消息原文进行加密得到新的MAC，比较新的MAC和随消息一起发送来的MAC，如果相同则未受到篡改

生成方法:

• 基于加密函数的认证码

 将消息分为64比特的小块，然后串联逐个加密

• 基于消息摘要（即散列函数） 

扩展：HMAC基于散列的消息认证码（Hash-based Message Authentication Code）

1.5 消息编码

基本思想：

• 引入冗余度，使得通过信道传送的可能序列集M大于消息集S（信源集）
• 发送方从M中选出用来代表消息的许用序列Li，即对消息进行编码
• 接收方根据编码规则，进行解码，还原出发送方按此规则向他传来的消息
• 窜扰者不知道编码规则，因而伪造的假码字多是M中的禁用序列，接收方将以很高的概率将其检测出来，并拒绝进行认证。

示例：

如果采用L0编码规则，则发送“00”代表信源0，发送“10"代表信源1，则消息：”01”和“11”是违法的，当接受方检测到01和11时，证明消息收到篡改。

2、数字签名

2.1  概述

概念：

附加在数据单元上的一些数据或是对数据做的密码变换，这种数据或变换可以被数据单元的接收者用来确认数据单元来源和数据单元的完整性，并保护数据不会被人伪造。

 从签名形式上分，可分为两种：

• 对整个消息的签名
• 对压缩消息的签名

主要目的：保证收方能够确认或验证发方的签名，但不能伪造；发送方发出签名消息后，不能否认所签发的消息

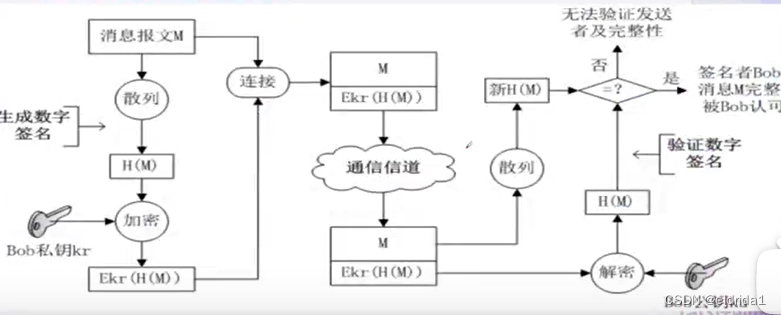
 2.2 基本流程

其中的加密的过程其实时生成签名的过程，其中用发送方的私钥加密，公钥解密

3、数字证书 

3.1 出现场景

在2的场景中，Bob用自己的私钥进行数字签名，Alice再拿Bob的公钥解密从而确认发送方身份。但是，在Bob发布自己公钥时，若被黑客拦截下来改为黑客自己的公钥，那么接收方就可能会将黑客发布的信息认为是Bob发布的信息，而Bob自己的信息则由于验证签名失败会被认为是遭篡改后的信息。

所以需要一个权威机构——CA机构（负责签发证书、认证证书、管理已颁发证书的机关）发布证书，证明Bob的公钥确实是Bob的

3.2 流程