51Nod-1491-黄金系统

ACM模版

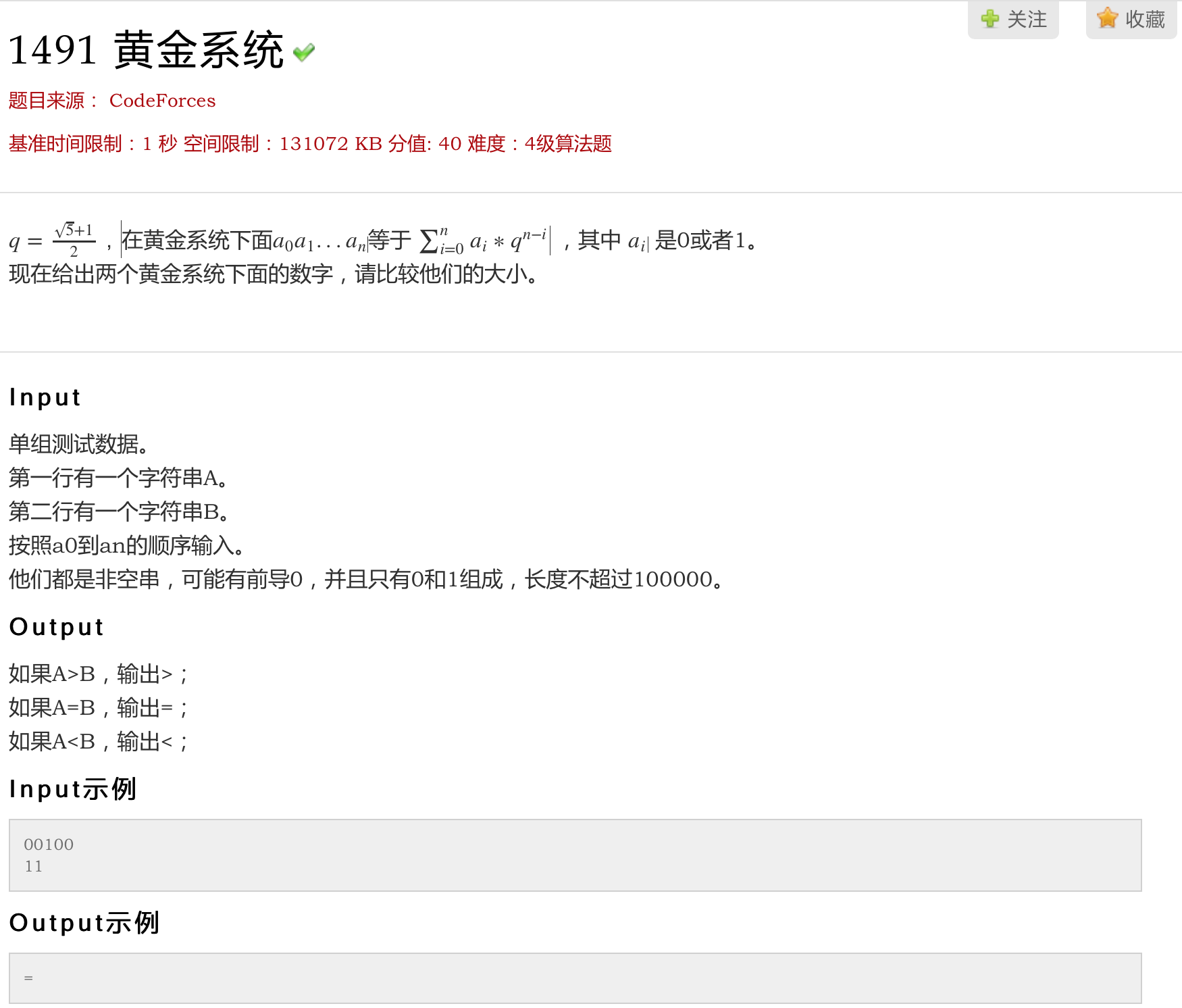
描述

题解

拿到这种题，不用多想，先枚举一些q^i，可以发现在某种程度上其符合斐波那契数列……
q^0用A表示，q^1用B表示，
我们可以发现，每一个数都可以用xA + yB表示，
而这里的x和y在一定程度上都符合斐波那契数列。
这也就给了我初始的想法，能否遍历一遍，
遇见连续两位都是1的时候就减去这两个1继而在高位添1，
就着这个想法尝试，这时注意到n-i的问题，
于是乎，想了一个办法就是在短的序列前补0，使两个序列长度一样，
接着，从后向前遍历。

此时问题又出现了，就是序列中会出现2的位，
可是在某种程度上，2会影响比大小，怎么才能避免出2呢？
经过观察发现，当连续1的个数为奇数时，最后会出现2，偶数则不会，
于是乎，加了一个判断，每次遇见一段儿1的时候先判断奇偶性，
如果是奇数，该位则不处理，直接跳过处理下一位，否则处理方案不变。

So，处理后的两个字符串中一定都是1和0，
且一定不存在连续的1（因为连续的可以组成更大的数），
那么从高位开始逐位比较，1的权重之和相等时，输出=，否则输出对应符号。
其实，并不需要求和，只用找最先出现的两者对应位置不同的情况就行了，
如果没有，就是相等了~~~KO.

代码

#include <iostream>
#include <cstring>

using namespace std;

const int MAXN = 1e5 + 5;

char A[MAXN];
char B[MAXN];

//  判断相连的1的奇偶性
bool judge(char C[], int i)
{
    int res = 0;
    while (C[i] == '1' && i > 0)
    {
        res++;
        i--;
    }
    return res % 2;
}

int main(int argc, const char * argv[])
{
    scanf("%s %s", A + 2, B + 2);
    A[0] = A[1] = B[0] = B[1] = '0';
    int lenA = (int)strlen(A);
    int lenB = (int)strlen(B);
    int len = lenA > lenB ? lenA : lenB;

    if (lenA < lenB)
    {
        int k = lenB - lenA;
        int pos = k;
        k += 2;
        for (int i = lenB - 1; i >= k; i--)
        {
            A[i] = A[i - pos];
        }
        for (int i = 2; i < k; i++)
        {
            A[i] = '0';
        }
    }
    else if (lenA > lenB)
    {
        int k = lenA - lenB;
        int pos = k;
        k += 2;
        for (int i = lenA - 1; i >= k; i--)
        {
            B[i] = B[i - pos];
        }
        for (int i = 2; i < k; i++)
        {
            B[i] = '0';
        }
    }
//    cout << A << '\n' << B << "\n\n";

    bool flag = true;
    for (int i = len - 1; i >= 2; i--)
    {
        if (A[i] == '0')
        {
            flag = true;
        }
        else if (A[i] == '1' && flag)
        {
            flag = false;
            if (judge(A, i))
            {
                continue;
            }
        }
        if (A[i] > '0' && A[i - 1] > '0')
        {
            A[i]--;
            A[i - 1]--;
            A[i - 2]++;
        }
    }

    flag = true;
    for (int i = len - 1; i >= 2; i--)
    {
        if (B[i] == '0')
        {
            flag = true;
        }
        else if (B[i] == '1' && flag)
        {
            flag = false;
            if (judge(B, i))
            {
                continue;
            }
        }
        if (B[i] > '0' && B[i - 1] > '0')
        {
            B[i]--;
            B[i - 1]--;
            B[i - 2]++;
        }
    }

//    cout << A << '\n' << B << "\n\n";

    for (int i = 0; i < len; i++)
    {
        if (A[i] != B[i])
        {
            if (A[i] > B[i])
            {
                cout << ">\n";
                return 0;
            }
            else
            {
                cout << "<\n";
                return 0;
            }
        }
    }
    cout << "=\n";

    return 0;
}