HDU-3938-Portal

ACM模版

描述

题解

必须说，这道题超出了我的英语水平，拆开了每个字母都认识，合起来，一半单词不认识，全篇，无尽懵逼……说得神马鬼！！！

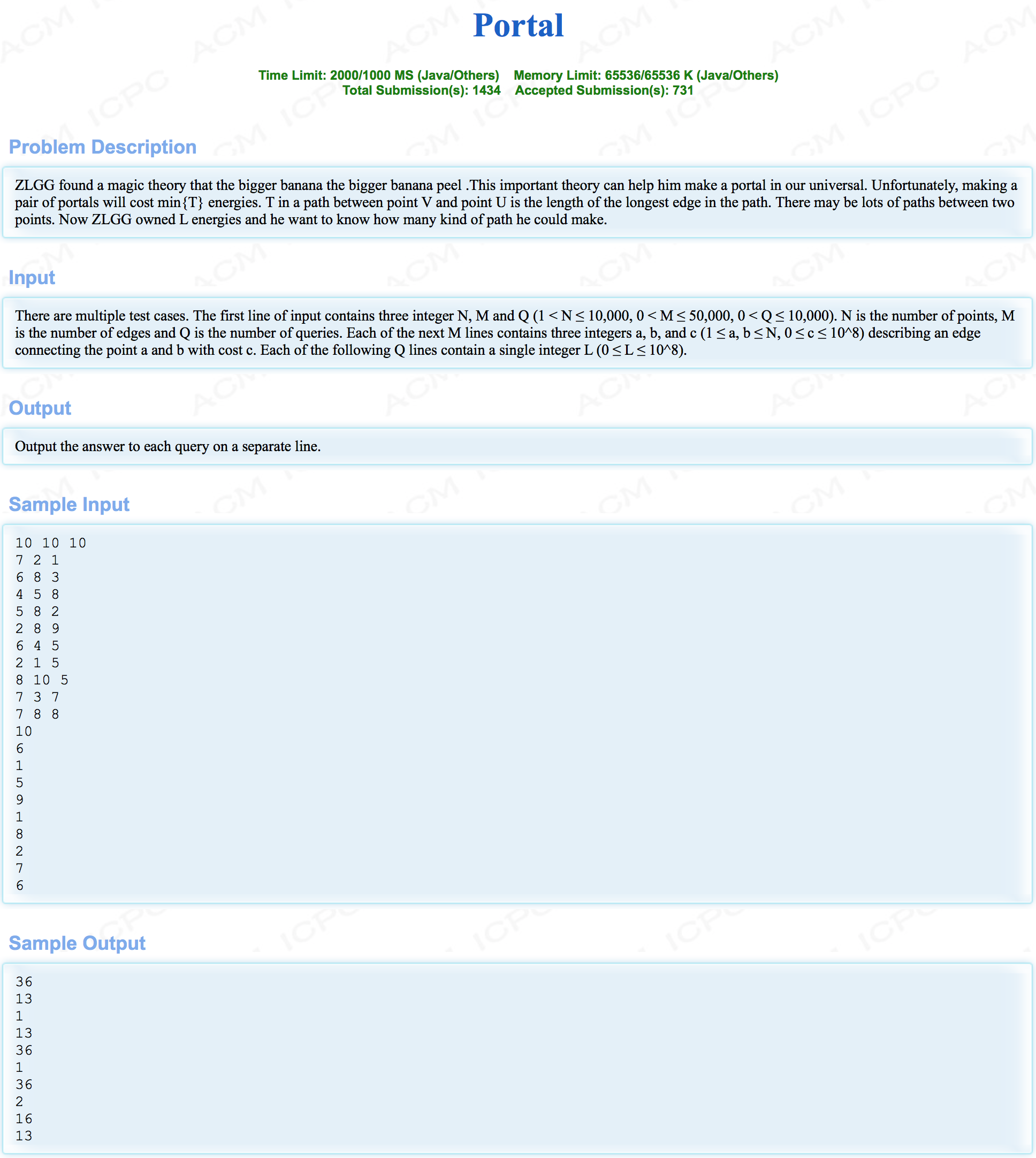
网上找了相关的题解，稍稍懂了些，是求满足点对儿之间路径存在最大花费段不超过q的点对儿数目，像克鲁斯卡尔，用并查集搞搞。

代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int MAXN = 50010;

struct edge
{
    int s, t, len;
};

struct order
{
    int id, q, res;
};

order Order[MAXN * 2];
edge Edge[MAXN];

int num[MAXN / 5];
int pre[MAXN / 5];
int out[MAXN];

bool cmp(edge a, edge b)
{
    return a.len < b.len;
}

int find(int x)
{
    int i = x, root;
    while (x != pre[x])
    {
        x = pre[x];
    }

    root = x;
    x = i;
    while (x != pre[x])
    {
        i = pre[x];
        pre[x] = root;
        x = i;
    }
    return root;
}

int join(int s, int t)
{
    int a = find(s);
    int b = find(t);

    int sum = 0;
    if (a != b)
    {
        //  不连通则进行连通并构成sum点对
        sum = num[a] * num[b];

        pre[b] = a;
        num[a] += num[b];
    }

    return sum;
}

bool cmp_(order a, order b)
{
    return a.q < b.q;
}

int main()
{
    int n, m, q;

    while (~scanf("%d%d%d", &n, &m, &q))
    {
        memset(Order, 0, sizeof(Order));

        for (int i = 0; i < m; i++)
        {
            scanf("%d%d%d", &Edge[i].s, &Edge[i].t, &Edge[i].len);
        }
        sort(Edge, Edge + m, cmp);

        for (int i = 0; i < q; i++)
        {
            scanf("%d", &Order[i].q);
            Order[i].id = i;
        }
        sort(Order, Order + q, cmp_);

        for (int i = 0; i <= n; i++)
        {
            pre[i] = i;
            num[i] = 1;
        }

        int cnt = 0;
        for (int i = 0; i < q; i++)
        {
            int ans = Order[i - 1].res;
            while (cnt < m && Edge[cnt].len <= Order[i].q)
            {
                int a = Edge[cnt].s;
                int b = Edge[cnt].t;
                ans += join(a, b);
                cnt++;
            }
            out[Order[i].id] = Order[i].res = ans;
        }
        for (int i = 0; i < q; i++)
        {
            printf("%d\n", out[i]);
        }
    }

    return 0;
}