Genetic Algorithm for VRP

Part 1: Representation and explanation of the given problem

This is a classical optimization problem in graphic thoery. Variable descriptions and mathmatical model are given below:

 

Variables:

K: the number of vehicles;

Q: capacity of each vehichle (all vehicles have the same capacity);

k: index of each vehicle;

S_k: length travelled by the kth vehicle;

N_k: the number of customers assigned to the kth vehicle;

M: the number of all customers;

x_mk: x coordination of the mth customer corresponding to the kth vehicle;

y_mk: y coordination of the mth customer corresponding to the kth vehicle;

D_mk: demand amount of the mth customer corresponding to the kth vehicle;

T_mk: arriving time of the mth customer corresponding to the kth vehicle;

T¹_mk: ready time of the mth customer corresponding to the kth vehicle;

T²_mk: due time of the mth customer corresponding to the kth vehicle;

T_k: the time when the kth vehicle returns to the original starting location;

T²₀: the total consuming time limit;

t: duration of sevice time ( same in all locations );

S: total distance of all vehicles;

n: the orignal index of the given location.

d_k(i , j): distance between the ith and jth location for the kth vehicle;

 

Analysis:

The goal is to fulfill demands of all customers at the lowest sum of travelling distances by all vehicles according to the problem requirement. For operational sake, all the customers have to be grouped into K sections. The kth section is supposed to contain N_k specific customers which are assigned to the kth vehicle.

 

Constraints can be listed in two aspects:

1.      number and volumes of the vehicles;

2.      time constraints including: ready time and due date of each customer and the total amount of time used by each vehicle. The latter one is mentioned in files as due date of the 0^th location.

 

 

Mathematical model:

 

Objective:

                                         

 

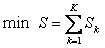
in which, we give the general mathematical notation of the optimization objective and overall restraints. Some detailed relations among these varialbes are stated as following:

      

where d(m,m+1) originally represents the distance between the mth and (m+1)th customer, yet the task description thinks that this is eaqual to the time consumed in the jounry between the two locations. As a result, we directly adopt d(m,m+1) as the time. t is the service time in the mth location for kth vehicle. The total time during the jouney of the kth vehicle T_k can be seen as the sum of 3 parts: 1 elasped time when the kth vehicle arrives the last customer N_k; 2 sevice duration at the N_kth location; 3 time used in the way from the N_kth location to the starting point.

 

Part 2: Genetic Algorithm for VRP

 

The mathematical model only lists the general relations among all the variables and give a overall description of the problem. However, several critical issues call for solutions:

1.      How to group these customers?

2.      For a certain group, how to choose the exact route?

In fact, the two issues are mutually reliant. If the former one can be solved, then VRP problem can be transformed into the TSP (Travelling Salesman Problem). Distances in certain routes will definitely influence the way to devide customers.

 

Chromosome generating:

 

The coding of VRP problem is quite different from norm problems. All the original chromosomes must obey all the constraints above, as a result, we are confromted with some chromosome structure problem.

 

1. Time restraint of all customers. We build a directional graph spanned by all the locations. We know that the p^th customer has a ready time T¹_p and a due time T²_p, there is a route from customer p to customer q only when

                                 

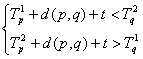
which describs that if there is a vehicle moves from customer p, with time consumed on the way to q^th customer and service time at location p taken into consideration, the time when the vehicle arrives at the q^th location must lie between the ready time and due time of the the q^th customer.

By this, we successfully transfer a complete graph into a directional graph whose degree is substantially decreased, and many routes need not to be considered.

2. Time constraint of a route. As is stated above, the time of traversing all the locations of a route and returning to the starting point must be less than the due time of the starting point. By further examination of some given examples and routine thinking we know that if there is no violation of the time restraint of the last customer of a route, the vehicle can return to the starting point on time.

3. Capacity limitation. In detailed operation, we will randomly choose a customer as the first customer of a certain route, and then there only some adjacent points next to it, from which we choose one as the second customer of the route, and so on. At each location, we will compute the cumulative demand of the customers on present route, a cease of the route when the cumulative demand exceeds the vehicle capacity. Then choose another customer as the first point of a new route and excute the same procedure. It must be addressed that each customer can only be contained in one route.

4. Constaint of the number of vehicles. We can excute the progress stated in Step 3, if the chromosome uses more vehicles than allowed, regenerate a new one until it satisfy all vehicle number constraint.

 

 

Estimation function:

 

Suppose there are M customers and K vehicles, there should be M+K+1 elements in the serial above. Our objective is to minimize the total distance, which in the specific serial can be expressed as the sum of all distances between two consecutive elements. I would like to choose such a calculation as fitness value.

                            

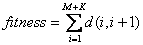
where i is the index in the serial and d(i, i+1) represents the distance between the i^th and (i+1)^th location.

 

Crossover and variation:

 

Crossover here are also barried by the structual problem (all the constraints), we can not merely choose a crossover point and exchange haves of two chromosomes as normal. As the problem is based on the directional graph, and then we need only think over constraints of capacity limitation and vehicle number.

We randomly choose two chromosomes from parental generation. We build a new directional graph among customers only(no consideration of the starting point), all the routes between points are selected from the two chromosomes. In fact, quite a lot are repeated in two chromosomes, each vertex has no more than two inputs and two outputs. Maybe some points are isolated (in two chromosomes the point is a route). Then we can simplify the directional graph. We firstly choose a shorter input of two-inputs point and desert the other one. Then choose a shorter output of two-outputs and let the other abandoned. With the redued graph, we furtherly generate the vehicle routes as above, in which capacity are taken account.

 

In each ieration, we randomly generate several chromosomes as variation.

 

Part3: Calculation result:

 

We choose the data listed in file “C1_2_1.txt” as an example.

Each generation 10 chromosomes are selected and 3 iterations are taken. We only give the exact chromosome with the best fitness.

 

Initial generation:

Index	1	2	3	4	5	6	7	8	9	10
Fitness (min)	4292.9	4601.7	5508.7	4791.8	4391.6	7438.8	7361.2	6563.2	5972.3	6705.4

Best fitness: 4292.9

Best chromosome:

Index	Route
1	0     20   41   12   129 11 6   122 90 67 17 39 0
2	0  21    23   182 75   163 194 145 195 52   92   0
3	0  24    61   139 0
4	0     30   120 19   192 196 97 14   89   105 15   59   0
5	0     32   171 65   86   115 94   51   110 162 0
6	0     45   155 0
7	0     144 119 166 35   126 71   9     1     99   53   0
8	0     100 64   179 109 149 56   0
9	0     57   5     10   193 46   128 106 167 34   95   158 0
10	0     114 159 38   150 22 151 16 140 187 142 111  63 0
11	0     73   116 147 160 47   91   70   0
12	0     78   175 13   43   2     0
13	0     190 82   0
14	0     85   80   31   25   172 77   0
15	0     93   55   18   54   185 132 7     181 188 108 0
16	0     101 0
17	0     133 48   26   152 40   153 169 96   130 28   74   107 0
18	0     118 83   143 176 36   33   121 165 49   0
19	0     148 103 197 124 141 69   200 174 136 189 0
20	0     161 104 0
21	0     164 66   0
22	0     170 134 50   156 112 168 79   29   87   42   123 198 0
23	0     177 3     88   8     186 127 98   157 0
24	0     178 27   173 154 0
25	0     135 58   184 199 37   81   138 137 183 0
26	0     180 84   191 125 4     72   0
27	0     44   102 146 0
28	0     60   0
29	0     62   0
30	0     68   76   0
31	0     113 0
32	0     117 0
33	0     131 0

 

Second generation:

Index

1

2

3