【59天|503.下一个更大元素II ● 42. 接雨水】

503.下一个更大元素II

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        stack<int> st;
        int n = nums.size();
        vector<int> res (n, -1);
        for(int i=0; i<2*n;i++)
        {
            while(!st.empty()&&nums[i%n]>nums[st.top()]){
                res[st.top()] = nums[i%n];
                st.pop();
            }
            st.push(i%n);
        }
        return res;
    }
};

42. 接雨水

height = [0,1,0,2,1,0,1,3,2,1,2,1]

假设我们遍历数组height， 那么以height[i] 为底可以接的雨水为多少呢？
这里我们可以推出一个很重要的公式： sum[i] = min(height[i]左边最高的边，height[i]右边最高的边) - height[i]；(sum[i] 表示height第i个元素可以接到的雨水)

例如： height[2] = 0； 左边的最大元素等于 1， 右边最大元素等于3. 求得height[2] 位置可以接的雨水为 min(1,3) -0 = 1;

1. 暴力法

按照上面的分析, 我们只需要遍历height， 然后求height[i] 左边的最大元素lmax和右边的最大元素rmax。

然后就可以按上面的公式计算出 height[i]可接住的雨水。最后用一个变量记录下这整个过程接的雨水就行。不难写出如下代码：

class Solution {
public:
    int trap(vector<int>& height) {
        int sum = 0;
        for (int i = 0; i < height.size(); i++) {
            // 第一个柱子和最后一个柱子不接雨水
            if (i == 0 || i == height.size() - 1) continue;

            int rmax = height[i]; // 记录右边柱子的最高高度
            int lmax = height[i]; // 记录左边柱子的最高高度
            for (int r = i + 1; r < height.size(); r++) {
            //从当前位置向右遍历，找到height[i] 的rHeight
                if (height[r] > rmax) rmax = height[r];
            }
            for (int l = i - 1; l >= 0; l--) {
            //从当前位置向左遍历，找到height[i] 的lHeight
                if (height[l] > lmax) lmax = height[l];
            }
            //按照公式计算height[i]接的雨水
            int h = min(lHeight, rHeight) - height[i];
            if (h > 0) sum += h;
        }
        return sum;
    }
};

时间复杂度o(n2), 空间复杂度O(1)。暴力的解法太费事，在leetcode是无法通过的。继续思考一下！

2. 动态规划

上述代码主要是在求 rmax、 lmax时花了太多时间。 我们可以考虑用一个额外空间记录每一个元素的 rmax, lmax。 然后在求雨水时到这里面取对应元素的 rmax 和 lmax即可。

求每个元素的rmax和lmax我们可以用动规的方法。
不难发现 lmax 满足如下规律：

lmax[i] = max(lmax[i-1], height[i]);  //(height.size()-1>i>0)
lmax[i] = 0; // i=0;

所以可以写出如下代码：

vector<int> lmax(height.size(), 0);
lmax[0] = height[0];
for (int i = 1; i < size; i++) {
	lmax[i] = max(height[i], lmax[i - 1]);
}

同理， 可求rmax数组。

rmax[size - 1] = height[size - 1];
for (int i = size - 2; i >= 0; i--) {
    rmax[i] = max(height[i], rmax[i + 1]);
}

最终整体代码为：

class Solution {
public:
    int trap(vector<int>& height) {
        if (height.size() <= 2) return 0;
        vector<int> lmax(height.size(), 0);
        vector<int> rmax(height.size(), 0);
        int size = height.size();

        // 记录每个柱子左边柱子最大高度
        lmax[0] = height[0];
        for (int i = 1; i < size; i++) {
            lmax[i] = max(height[i], lmax[i - 1]);
        }
        // 记录每个柱子右边柱子最大高度
        rmax[size - 1] = height[size - 1];
        for (int i = size - 2; i >= 0; i--) {
            rmax[i] = max(height[i], rmax[i + 1]);
        }
        // 求和
        int sum = 0;
        for (int i = 0; i < size; i++) {
            int count = min(lmax[i], rmax[i]) - height[i];
            if (count > 0) sum += count;
        }
        return sum;
    }
};

我们发现时间复杂度减低为O(n), 但是空间复杂度增大到O(n).这样写是可以通过这题的.

3. 双指针

我们进一步优化一下, 考虑如何不要额外空间去解决这题.

我们回到题目一开始时,我们推出的那个重要公式:
sum[i] = min(lmax[i], rmax[i]) - height[i];

从这个公式可以知道,如果想求sum[i] 那么必须得知道lmax[i] 和rmax[i]
其中, lmax[i] 其实可以在从左到右遍历height得过程中, 通过动规一样的思路求得.

lmax = max(height[left], lmax);

rmax[i] 由于height[i] 右边的元素都还是遍历到,所以是不可能求到的.

那么我们思考一下, 我们不知道rmax[i]等于多少, 但是如果能保证rmax[i] >= lmax[i] 是不是也能求出sum[i]? 此时, sum[i] = lmax[i]-height[i];

于是, 我们尝试从rmax[i]的动规规律中找到能保证rmax[i] >= lmax[i]的条件:

rmax[i] = max(height[i], rmax[i + 1]);// 已知的动规规律
即, rmax[i] >= rmax[i+1] >= .... >= rmax[height.size()-1]; 
即, rmax[i] >= rmax[j] // j>i

同理可得, lmax[j] >= lmax[i] // j>i

如果想让rmax[i] >= lmax[i], 由于rmax[i] >= rmax[j] ,
所以当rmax[j] > lmax[i]时, 就能保证rmax[i] >= lmax[i]. 此时 sum[i] = lmax[i]-height[i];

那么当rmax[j]<= lmax[i]时是什么情况呢?
由于lmax[j] >= lmax[i], 那么 lmax[j]>=rmax[j] 恒成立. 有 sum[j] = rmax[j]-height[i];

综上, 若rmax[j] > lmax[i], sum[i] = lmax[i]-height[i];
若rmax[j]<= lmax[i], sum[j] = rmax[j]-height[i];

画个图加深理解:

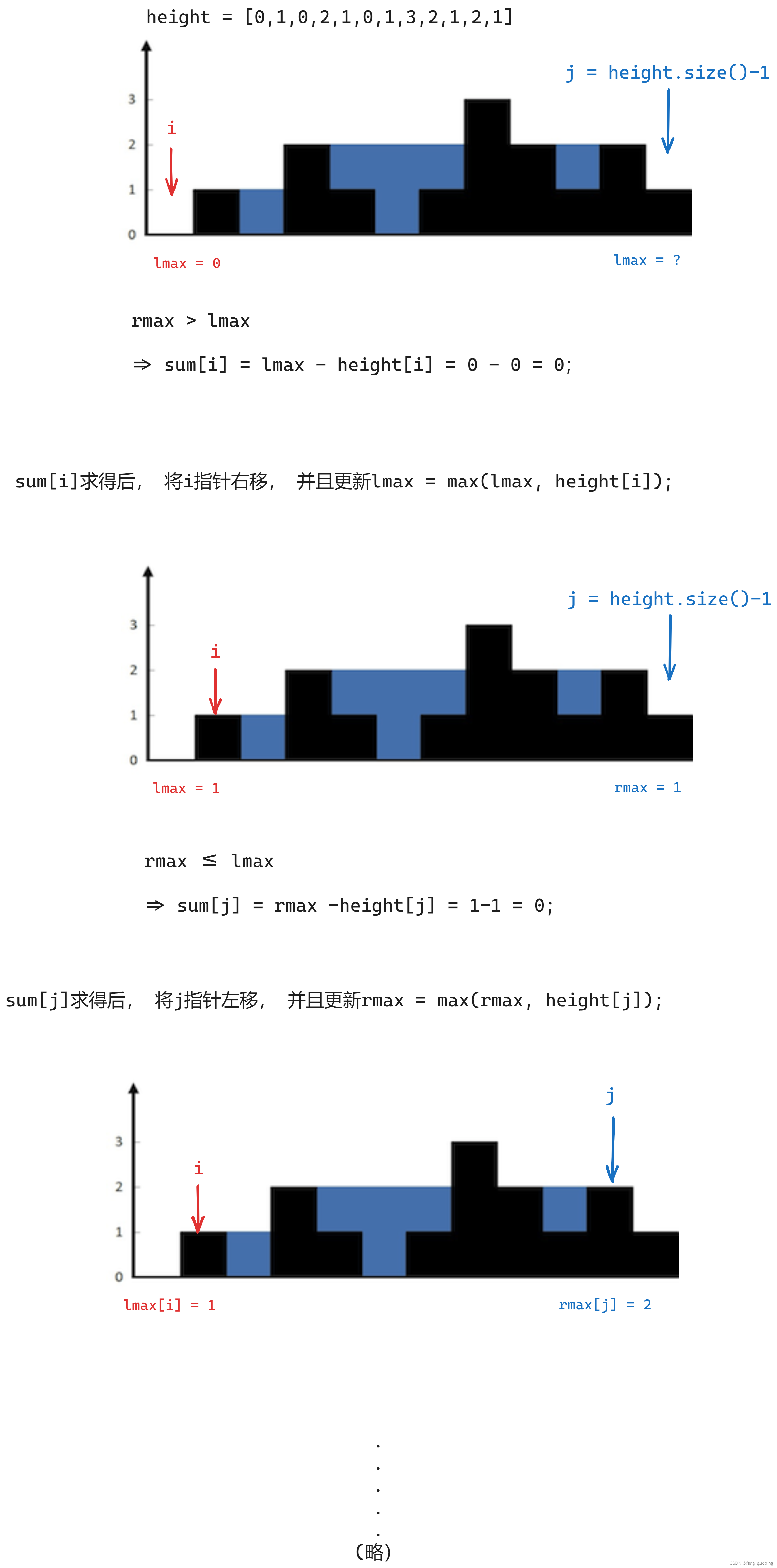
分析到这一步其实很明显了,这就是首尾指针的题.

如果首指针的lmax < 尾指针的rmax, 那么sum[i] = lmax-height[i], 然后首指针右移;
否则首指针的lmax >= 尾指针的rmax, 即尾指针的rmax<=首指针的lmax, 那么sum[j] = rmax - height[i], 然后尾指针左移.
重复这个过程, 直到首尾指针相遇.

class Solution {
public:
    int trap(vector<int>& height) {
        int left = 0, right = height.size()-1;
        int left_lmax = 0, right_rmax = 0;
        int res =0;
        while(left<right)
        {   
            left_lmax = max(height[left], left_lmax);
            right_rmax = max(height[right], right_rmax);
            if(left_lmax<right_rmax)
            {
                res += left_lmax - height[left];
                left++;
            }
            else{//right_rmax <= left_lmax
                res += right_rmax - height[right];
                right--;
            }
        }
        return res;
    }
};

时间复杂度O(n), 空间复杂度O(1)

4. 单调栈

单调栈求雨水的思路和公式跟上面提到的三种方法不一样.单调栈的解法可以看卡哥的单调栈.

class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> st;
        st.push(0);
        int sum = 0;
        for (int i = 1; i < height.size(); i++) {
            while (!st.empty() && height[i] > height[st.top()]) {
                int mid = st.top();
                st.pop();
                if (!st.empty()) {
                    int h = min(height[st.top()], height[i]) - height[mid];
                    int w = i - st.top() - 1;
                    sum += h * w;
                }
            }
            st.push(i);
        }
        return sum;
    }
};

时间复杂度O(n), 空间复杂度O(n)