HDU 3220 Alice’s Cube 按位压缩表示状态+BFS

Alice’s Cube

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1948    Accepted Submission(s): 639

Problem Description

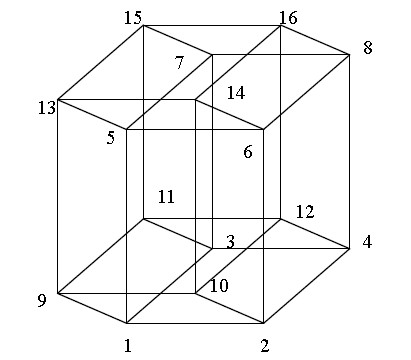
Alice has received a hypercube toy as her birthday present. This hypercube has 16 vertices, numbered from 1 to 16, as illustrated below. On every vertex, there is a light bulb that can be turned on or off. Initially, eight of the light bulbs are turned on and the other eight are turned off. You are allowed to switch the states of two adjacent light bulbs with different states (“on” to “off”, and “off” to “on”; specifically, swap their states) in one operation.

Given the initial state of the lights, your task is to calculate the minimum number of steps needed to achieve the target state, in which the light bulbs on the sub cube (1,2,3,4)-(5,6,7,8) are turned off, and the rest of them are turned on.

 

Input

There are multiple test cases. The first line of the input contains an integer T, meaning the number of the test cases. There are about 13000 test cases in total.
For each test case there are 16 numbers in a single line, the i-th number is 1 meaning the light of the i-th vertex on the picture is on, and otherwise it’s off.

 

Output

For every test cases output a number with case number meaning the minimum steps needed to achieve the goal. If the number is larger than 3, you should output “more”.

 

Sample Input

  
  

   
   3
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
0 1 0 0 0 0 0 0 1 0 1 1 1 1 1 1
0 0 0 0 0 0 1 0 1 0 1 1 1 1 1 1
  
  

 

Sample Output

  
  

   
   Case #1: 0
Case #2: 1
Case #3: more
  
  

bfs的套路

1，首先正难则反，因为终止状态已经确定了，就是0000000011111111，所以可以终止状态往前搜索（3步即可）。

2，标记，用数字的二进制表示哪些状态已经被访问过了，一个bool vis[1<<16]的数组即可

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<set>
using namespace std;
struct node {
    int a[17];
    int step;
};
node h;
bool vis[1<<16];///2^16
int st[1<<16];
int data[17][4]={
    {0,0,0,0},
    {2,3,5,9},
    {1,4,6,10},
    {1,4,7,11},
    {2,3,8,12},
    {1,6,7,13},
    {2,5,8,14},
    {3,5,8,15},
    {4,6,7,16},
    {1,10,11,13},
    {2,9,12,14},
    {3,9,12,15},
    {4,10,11,16},
    {5,9,14,15},
    {6,10,13,16},
    {7,11,13,16},
    {8,12,14,15}
};
int getstate(int a[]){
    int sum=0;
    int r=1;
    for(int i=1;i<=16;i++){
        sum+=(a[i]*r);
        r*=2;
    }
    return sum;
}
void bfs(){
    queue<node> qq;
    h.a[1]=0;h.a[2]=0;h.a[3]=0;h.a[4]=0;
    h.a[5]=0;h.a[6]=0;h.a[7]=0;h.a[8]=0;
    h.a[9]=1;h.a[10]=1;h.a[11]=1;h.a[12]=1;
    h.a[13]=1;h.a[14]=1;h.a[15]=1;h.a[16]=1;
    h.step=0;
    vis[getstate(h.a)]=true;
    st[getstate(h.a)]=0;
    qq.push(h);
    while(!qq.empty()){
        node top;
        top=qq.front();
        qq.pop();
        if(top.step==3){
            continue;
        }
        int temp[17];
        //memcpy(temp,top.a,sizeof(temp));
        for(int i=1;i<=16;i++){
            for(int j=0;j<4;j++){
                memcpy(temp,top.a,sizeof(temp));
                if(temp[i]!=temp[data[i][j]]){
                    swap(temp[i],temp[data[i][j]]);
                    if(vis[getstate(temp)]){
                        continue;
                    }else{
                        vis[getstate(temp)]=true;
                        st[getstate(temp)]=top.step+1;
                        node newnode;
                        memcpy(newnode.a,temp,sizeof(temp));
                        newnode.step=top.step+1;
                        qq.push(newnode);
                    }
                }
            }
        }

    }

}
int main(){
    int T;
    memset(vis,false,sizeof(vis));
    memset(st,0,sizeof(st));
    bfs();///end state fix
    int cas=1;
    scanf("%d",&T);
    while(T--){
        int sum;
        int s[17];
        for(int i=1;i<=16;i++){
            scanf("%d",&s[i]);
            sum=getstate(s);
        }
        if(vis[sum]){
            printf("Case #%d: %d\n",cas++,st[sum]);
        }else{
            printf("Case #%d: more\n",cas++);
        }
    }
    return 0;
}