【题解】LeetCode-寻找两个有序数组的中位数（median-of-two-sorted-arrays）

4. 寻找两个有序数组的中位数

给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。

请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。

你可以假设 nums1 和 nums2 不会同时为空。

示例 1:

nums1 = [1, 3]
nums2 = [2]

则中位数是 2.0
示例 2:

nums1 = [1, 2]
nums2 = [3, 4]

则中位数是 (2 + 3)/2 = 2.5

思路一
对于这样的题很自然的想法是：先合并，再求中位数。可是仔细想想似乎不满足题干对时间复杂度的要求，因为合并所需要的时间是O(N)，其中N = m + n，且在空间上也会有额外的消耗。显然这不是最优的解法。（不过后来翻评论发现有哥们这样做，而且基本都过了？？？）

解法一
可以参考归并排序的merge部分，这里就不做探讨了。

思路二
很惭愧，翻了题解~
值得一说的是，笔者发现官方对这道题的解法数学味有点浓，于是花了点时间研究了一波，下面是一些收获：

先明确一下概念：中位数把一组有序的数列划分成两个数量级相当的子集，左子集恒小于等于右子集。
什么意思呢？翻译成伪代码就是：

1. COUNT(Left) == COUNT(Right);
2. ANY(Left) <= ANY(Right);

咋一看好像没什么卵用，仔细一想其实不然，这个概念是可逆的，也就是说：如果某个数满足这个概念，则其就是要找的中位数。

那么不妨假设在第一个有序数集A中找到了一个下标为x的数把A划分为等量的两份，在数集B中找到的划分点下标为y，画图形象化就是：

                   |
     A[0]...A[x-1] | A[x]...A[m-1]
B[0],B[1]...B[y-1] | B[y],B[y+1]...B[n-1]
                   |

搞清楚了这个，就可以按图索骥了：

第一步、根据第一个等量关系可以推导出：

• 当m + n为偶数时，(COUNT(A.Left) + COUNT(B.Left) = x + y) == (COUNT(A.Right)+COUNT(B.Right) = m - x + n - y)
• 当m + n为奇数时，(COUNT(Left) = x + y) == (COUNT(Right) = m - x + n - y + 1)
  也就是说：$ 2(x+y) = m + n + (m + n)%2 $即：$ y = {{ m + n + {(m + n)} % 2 } \over 2} - x $
  函数形如：
  

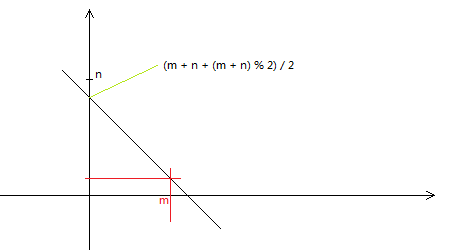
第二步、利用第一步分析结果：枚举一个x就可以得到一个y,这个时候还需要满足条件2：
由于A和B初始是有序的: A[x-1] <= A[x]，B[y-1] <= B[y];
此时若A[x-1] <= B[y] 且 B[y-1] <= A[x]，则就相当于满足了条件2。

第三步、找到x和y后如何得到最终的中位数呢？
通过举例的方式很快可以发现：

• 当m + n为奇数时，ans = Max(A[x-1], B[y-1])；
• 当m + n为偶数时，ans = (Max(A[x-1], B[y-1]) + Min(A[x], B[y]))/2；

解法二

class Solution {
    public double findMedianSortedArrays(int[] A, int[] B) {
        int m = A.length, n = B.length;
        if (m > n) { // 保证 m <= n, 确保j>=0
            int t = m;
            int[] T = A;
            m = n;
            A = B;
            n = t;
            B = T;
        }

        int a = 0, b = m, len = m + n;
        int halfLen = (len + (len) % 2) / 2;
        int x, y;

        while (a <= b) {
            x = a + (b - a) / 2;
            y = halfLen - x;
            if (x > a && A[x - 1] > B[y]) { // x取得太大了
                b = x - 1;
            } else if (x < b && A[x] < B[y - 1]) { // x取得太小了
                a = x + 1;
            } else { // x,y满足了条件2
                int left;
                if (x <= 0) {
                    left = B[y - 1];
                } else if (y <= 0) {
                    left = A[x - 1];
                } else {
                    left = Math.max(A[x - 1], B[y - 1]);
                }

                if ((len) % 2 == 1) {
                    // m+n为奇数
                    return left;
                }


                int right;
                if (x >= m) {
                    right = B[y];
                } else if (y >= n) {
                    right = A[x];
                } else {
                    right = Math.min(A[x], B[y]);
                }
                // m+n为偶数
                return (left + right) / 2.0;

            }
        }
        return 0.0;
    }
}

其实可以发现，这个代码好像跟官方的解答一毛一样哎~