Splay学习笔记

昨天这个时候到现在终于把Splay给搞明白了，还A了一道郁闷的出纳员；刚学完的感受：我再也不碰这东西了；做完郁闷的出纳员的感受：我发誓这辈子不当出纳员(虽然这确实只是个入门题……)
于是来讲一讲这个恶心的东西吧……(全程不用指针，请做好心理准备……)
学习前请先学习下二叉搜索树，里面可能直接用到这个东西
首先，Splay是一个数据结构，为了突出它是一个数据结构，所以给他开个结构体……

struct tree
{
    int val,sz,cnt;//val为值 sz为子树大小，cnt为"有多少这个值"
    //cnt:假如出现了两个一模一样的值，只需要让cnt+1就可以了，cnt是数目
    int s[2],f;//s[0]为左儿子 s[1]为右儿子 f为父亲
};

为了之后的操作，我们再写三个函数(如果认为没用可以先跳过，过一会用到了再回来看)

bool son(int x) //返回x是左儿子还是右儿子，如果为左儿子，返回0，右儿子则返回1
{
    return a[a[x].f].s[1] == x;
}

void rejs(int x)    //重新计算以x为根，子树的大小，子树大小等于左子树大小加右子树大小(好吧我承认我英语拙计)
{
    a[x].sz = a[a[x].s[0]].sz + a[a[x].s[1]].sz + a[x].cnt;
}

void point(int x,int y,bool z)  //在x下面插入y，y是x的z儿子(z为0则左儿子，z为1为右儿子)
{
    a[x].s[z] = y;
    a[y].f = x;
}

写完这几个树的基本函数，我们要开始讲splay啦(似乎我之前好像真的没有开始讲splay)
Splay最重要的一个操作就是旋转(rotate)，如下，(图片为1600x900，可直接作为桌面)：

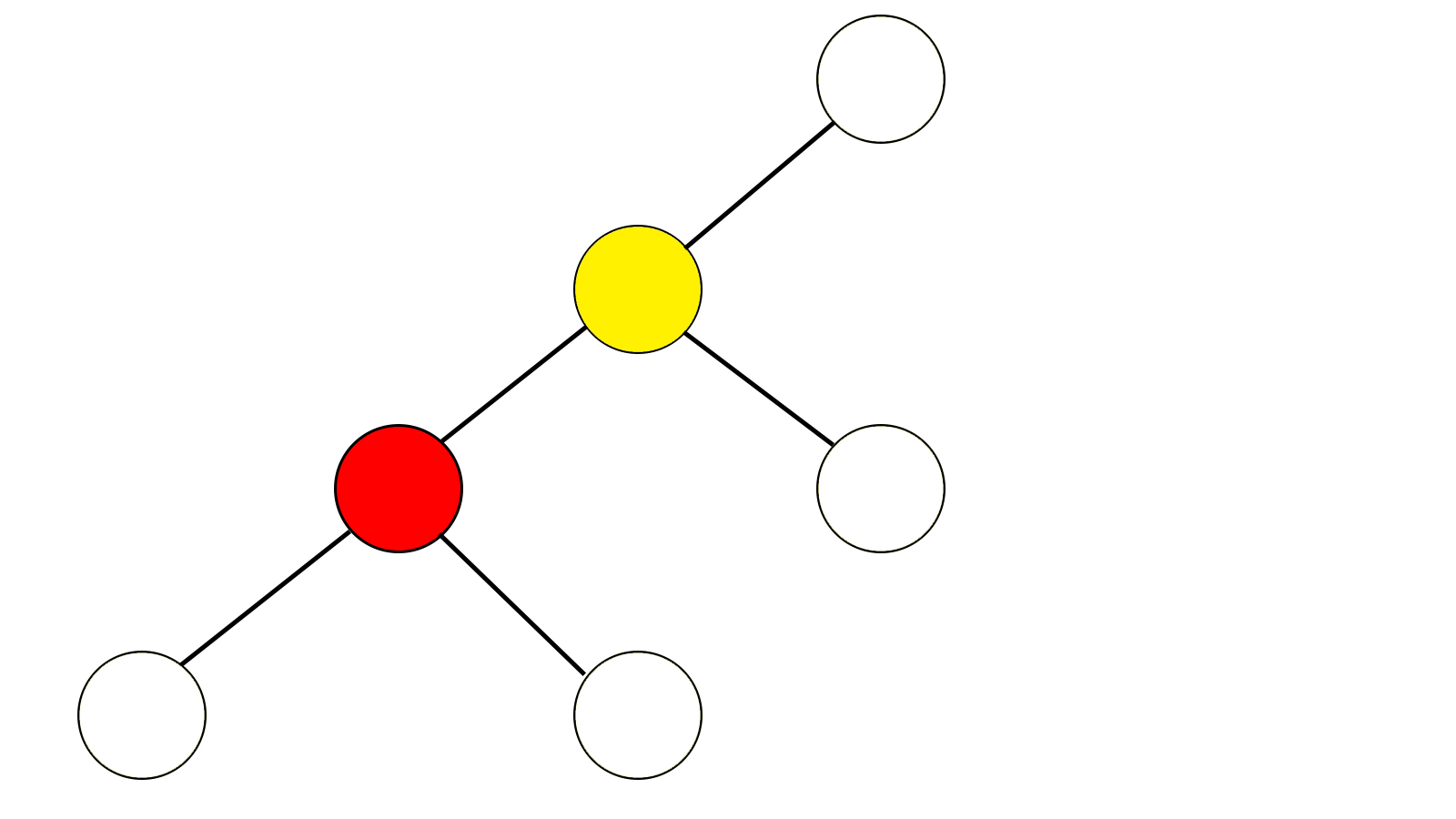
我们的目的是将红色节点旋转到它父亲的位置，即黄色节点的位置
我们应当怎么办呢？不要急，看组图

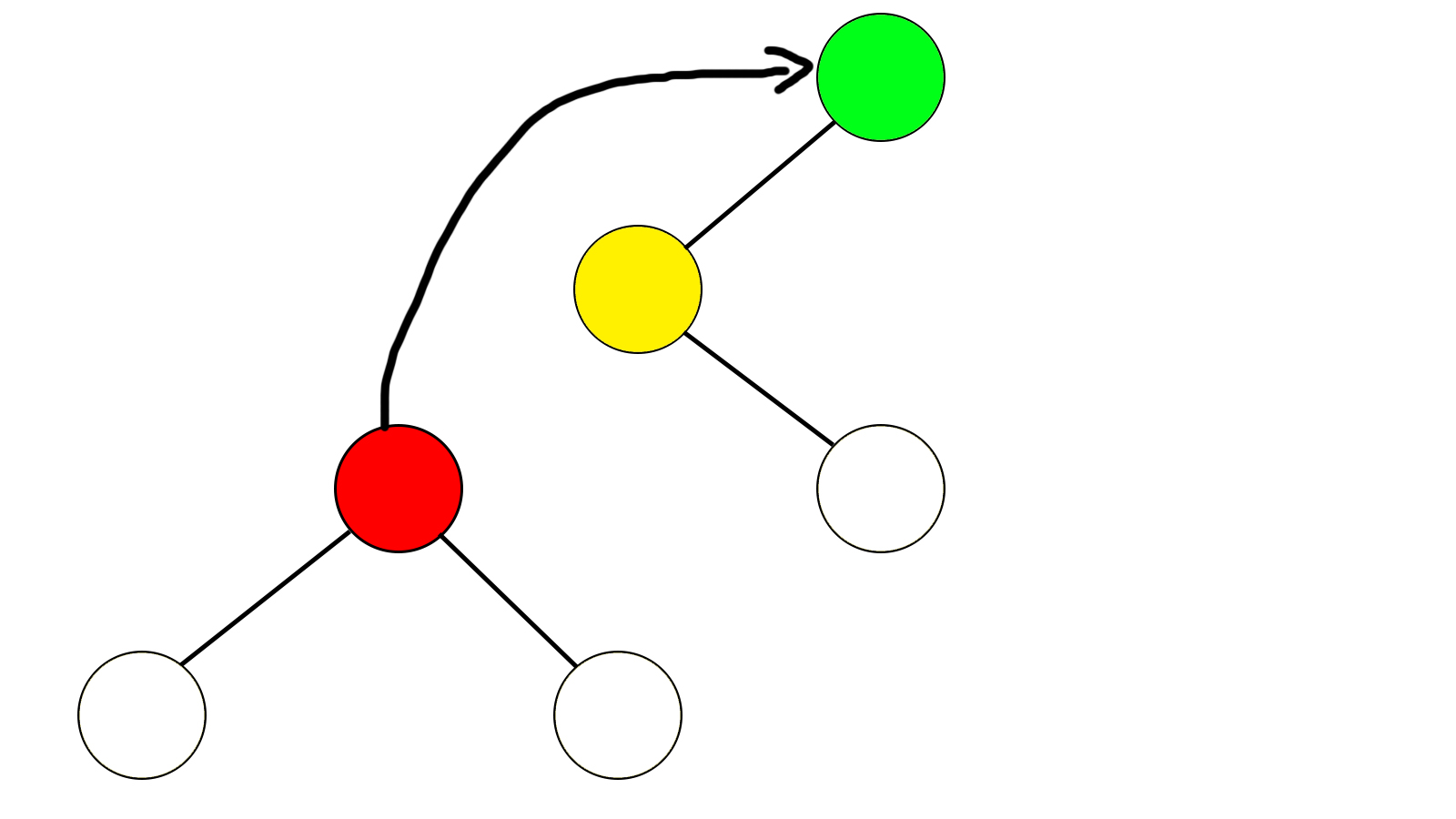
bool型变量son(黄)代表黄色节点是左儿子还是右儿