线段树(Segment Tree)是一种二叉搜索树,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
对于线段树中的每一个非叶子节点[a,b],它的左子树表示的区间为[a,(a+b)/2],右子树表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树。叶节点数目为N,即整个线段区间的长度。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。而未优化的空间复杂度为2N,因此有时需要离散化让空间压缩。
基本操作
给定整个线段区间,建立一棵线段树的时间复杂度是 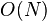 。单点修改的时间复杂度是
。单点修改的时间复杂度是 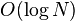 。单点查询的时间复杂度是
。单点查询的时间复杂度是  。如果允许惰性赋值而加上延迟标记的话,许多的区间修改的时间复杂度也会是
。如果允许惰性赋值而加上延迟标记的话,许多的区间修改的时间复杂度也会是 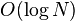 ,但是单点查询的时间复杂度会变成
,但是单点查询的时间复杂度会变成 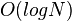 。
。
代码中, rt指的是root, 当前子树的根节点; l, r指的是当前子树所统计的区间![[l, r]](http://upload.wikimedia.org/math/a/6/1/a615eebe867a499ba18a5de92492cf93.png) 利用完全二叉堆的性质来保存节点编号, 所以rt << 1是左子树的节点, rt << 1 | 1是右子树的节点 在查询和成端更新操作中的L和R是指修改或者查询的区间
利用完全二叉堆的性质来保存节点编号, 所以rt << 1是左子树的节点, rt << 1 | 1是右子树的节点 在查询和成端更新操作中的L和R是指修改或者查询的区间
------wiki
由于线段树维护了一个区间,可以快速的对该区间进行查改操作,因此适用于对区间进行频繁查改操作的算法。如果只对区间进行求和操作而不修改则应该考虑其它的算法,比如:如果频繁求某个给定区间的和,但是区间的值永远不变,则应该利用公式:sum[m,n] = sum[1,n]-sum[1,m-1]。从而只需要保存:sum[i],i form 0 - N 即可。该方法无论从时间还是空间均比线段树要好。正如刘未鹏大神所说:联想很重要,但是我们应该多利用推理来求解答案。
树状数组:
数组a[1..n],那么查询a[1]+...+a[n]的时间是log级别的,而且是一个在线的数据结构,支持随时修改某个元素的值,复杂度也为log级别。
来观察这个图:

树状数组的结构图
令这棵树的结点编号为C1,C2...Cn。令每个结点的值为这棵树的值的总和,那么容易发现:
C1 = A1
C2 = A1 + A2
C3 = A3
C4 = A1 + A2 + A3 + A4
C5 = A5
C6 = A5 + A6
C7 = A7
C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
...
C16 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9 + A10 + A11 + A12 + A13 + A14 + A15 + A16
这里有一个有趣的性质:
设节点编号为x,那么这个节点管辖的区间为2^k(其中k为x二进制末尾0的个数)个元素。因为这个区间最后一个元素必然为Ax,
所以很明显:Cn = A(n – 2^k + 1) + ... + An
算这个2^k有一个快捷的办法,定义一个函数如下即可:
|
1
2
3
|
intlowbit(intx){
returnx&(x^(x–1));
}
|
利用机器补码特性,也可以写成:
|
1
2
3
|
intlowbit(intx){
returnx&(-x);
}
|
当想要查询一个SUM(n
)(求a[n]的和),可以依据如下算法即可:
step1: 令sum = 0,转第二步;
step2: 假如n <= 0,算法结束,返回sum值,否则sum = sum + Cn,转第三步;
step3: 令n = n – lowbit(n),转第二步。
可以看出,这个算法就是将这一个个区间的和全部加起来,为什么是效率是log(n)的呢?以下给出证明:
n = n – lowbit(n)这一步实际上等价于将n的二进制的最后一个1减去。而n的二进制里最多有log(n)个1,所以查询效率是log(n)的。
那么修改呢,修改一个节点,必须修改其所有祖先,最坏情况下为修改第一个元素,最多有log(n)的祖先。
所以修改算法如下(给某个结点i加上x):
step1: 当i > n时,算法结束,否则转第二步;
step2: Ci = Ci + x, i = i + lowbit(i)转第一步。
i = i +lowbit(i)这个过程实际上也只是一个把末尾1补为0的过程。
------百度百科
之前一直想不明白为什么第二步是 i = i + lowbit(i)。没办法很好地感知,但是我有不想死记。后来终于想到了证明方法了
证:
设下一步的 i 的增量为 k,则当 k 小于 lowbit(i) 的时候,必有 lowbit(k+i) < lowbit(i) 且 lowbit(k+i) == lowbit(k)
又 C(k+i) = A( k+i - lowbit(k+i) + 1 )....+ A(k+i)。即
C(k+i) = A( k+i - lowbit(k) + 1 )....+ A(k+i)
而 k+i - lowbit(k) +1 > i 所以 C(k+i) 不需要更新,同理易得最小的增量是 lowbit(i)
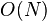 。单点修改的时间复杂度是
。单点修改的时间复杂度是 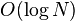 。单点查询的时间复杂度是
。单点查询的时间复杂度是  。如果允许惰性赋值而加上延迟标记的话,许多的区间修改的时间复杂度也会是
。如果允许惰性赋值而加上延迟标记的话,许多的区间修改的时间复杂度也会是 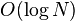 ,但是单点查询的时间复杂度会变成
,但是单点查询的时间复杂度会变成 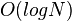 。
。![[l, r]](http://upload.wikimedia.org/math/a/6/1/a615eebe867a499ba18a5de92492cf93.png) 利用完全二叉堆的性质来保存节点编号, 所以rt << 1是左子树的节点, rt << 1 | 1是右子树的节点 在查询和成端更新操作中的L和R是指修改或者查询的区间
利用完全二叉堆的性质来保存节点编号, 所以rt << 1是左子树的节点, rt << 1 | 1是右子树的节点 在查询和成端更新操作中的L和R是指修改或者查询的区间






















 4640
4640

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








