2023年CSP-J第一轮认证试题解析

最新推荐文章于 2024-08-27 07:54:02 发布

Easoncalm

最新推荐文章于 2024-08-27 07:54:02 发布

阅读量2.6k

点赞数

文章标签： c++

本文链接：https://blog.csdn.net/ffalali001/article/details/133487218

版权

单项选择

1.在C++中，下面哪个关键字用于声明一个变量，其值不能被修改? ( )

A. unsigned

B. const

C. static

D. mutable

【答案】B

【考点】考点: C++语法知识: 变量与常量

【解析】变量是存储信息的容器，变量在计算机内有一个内存地址，里面放的内容即变量的值，变量是允许被修改，但是常量的值不允许被修改，常量的定义格式如下:

const 数据类型常量名 = 常量值;

数据类型 const 常量名 = 常量值;

题目说其值不能被修改指的是常量，因此选择 const 修饰，所以答案选择 B。

2. 八进制数 12345670 和 07654321 的和为 ( )

A. 22222221

B. 21111111

C. 22111111

D. 22222211

【答案】D

【考点】进制转换 (初赛集训内容)

【解析】R 进制的运算逢 R 进一，题目是八进制加法，所以每一个进制位上的数字是逢 8 进一。

12345670

+ 07654321

--------------

22222211

3. 阅读下述代码，请问修改 data 的 value 成员以存储 3.14，正确的方式是( )

union Data{ int num; float value; char symbol;};union Data data;

A. data.value = 3.14;

B. value.data = 3.14;

C. data->value = 3.14;

D. value->data = 3.14;

【答案】A

【考点】联合体(NOI新大纲内容)

【解析】共用体定义格式:

union 共用体名{    成员列表};

共用体的所有成员占用同一段内存，修改一个成员会影响其余所有成员。

共用体占用的内存等于最长的成员占用的内存。

共用体使用了内存覆盖技术，同一时刻只能保存一个成员的值，如果对新的成员赋值，就会把原来成员的值覆盖掉。

题目中 data 占用 4 个字节，修改 value 使用 . 运算符，-> 适用于指针。

4. 假设有一个链表的节点定义如下：

struct Node {    int data;         Node* next;};

现在有一个指向链表头部的指针：Node* head。如果想要在链表中插入一个新节点，其成员 data 的值为 42，并使新节点成为链表的第一个节点，下面哪个操作是正确的? ( )

A. Node* newNode = new Node; newNode->data = 42; newNode->next = head; head = newNode;B. Node* newNode = new Node; head->data = 42; newNode->next = head; head = newNode;C. Node* newNode = new Node; newNode->data = 42; head->next = newNode;D. Node* newNode = new Node; newNode->data = 42; newNode->next = head;

【答案】A

【考点】链表的插入(数据结构)

【解析】题目使用头插法即可

B. 赋值错误。

C. 新插入的结点的后继未确认。

D. 表头结点的后继未指向新生成的结点。

5. 根节点的高度为 1，一根拥有 2023 个节点的三叉树高度至少为 ( )

A. 6

B. 7

C. 8

D. 9

【答案】C

【考点】树

【解析】观察下图 👇

第 1 层有 1 个结点

第 2 层有 3 个结点

第 3 层有 27 个结点

......

第 n 层有 3n 个结点

根据性质知道是一个等比数列，公比为 3，根据等比数列求和公式:

计算过程如下:

6. 小明在某一天中依次有七个空闲时间段，他想要选出至少一个空闲时间段来练习唱歌，但他希望任意两个练习的时间段之间都有至少两个空闲的时间段让他休息，则小明一共有（）种选择时间段的方案。

A. 31

B. 18

C. 21

D. 33

【答案】B

【考点】枚举法

【解析】枚举的方法讲解

① 只有一个练习时间段的情况

② 只有两个练习时间段的情况

③ 只有三个练习时间段的情况

7. 以下关于高精度运算的说法错误的是( )

A. 高精度计算主要是用来处理大整数或需要保留多位小数的运算

B. 大整数除以小整数的处理的步骤可以是，将被除数和除数对齐，从左到右逐位尝试将除数乘以某个数，通过减法得到新的被除数，并累加商

C. 高精度乘法的运算时间只与参与运算的两个整数中长度较长者的位数有关。

D. 高精度加法运算的关键在于逐位相加并处理进位。

【答案】C

【考点】高精度运算

【解析】高精度乘法的时间取决于两个大整数的长度的乘积有关，高精度乘低精度 O(n) 的时间复杂度，高精度乘高精度 O(n*n) 的时间复杂度。

8. 后缀表达式“6 2 3 + - 3 8 2 / + * 2 ^ 3 +”对应的中缀表达式是 ( )

A. ((6 - (2 + 3)) * (3 + 8 / 2)) ^ 2 + 3

B. 6 - 2 + 3 * 3 + 8 / 2 ^ 2 + 3

C. (6 - (2 + 3)) * ((3 + 8 / 2) ^ 2) + 3

D. 6 - ((2 + 3) * (3 + 8 / 2)) ^ 2 + 3

【答案】A

【考点】栈的应用

【解析】首先 6，2，3 入栈，遇到第一个操作符 +，弹出 2 和 3 执行加法，然后将 2 + 3 的结果入栈，遇到操作符 -，弹出两个数 6 和 (2 + 3) 执行减法，然后将 (6 - (2 + 3)) 的结果入栈，3，8，2 依次入栈，遇到操作符 /，弹出 2 和 8 执行除法，然后将 8/2 入栈，遇到操作符 +，弹出 8/2 和 3 执行加法，然后将 (3 + 8/2) 入栈，遇到操作符 *，弹出 (6 - (2 + 3)) 和 (3 + 8/2) 执行乘法，然后将 (6-(2 + 3))*(3 + 8/2) 入栈，然后 2 入栈，遇到操作符 ^ 弹出 2 和 (6-(2 + 3))*(3 + 8/2) 执行异或操作，然后将 (6-(2 + 3))*(3 + 8/2)^2 入栈，然后 3 入栈，遇到操作符 +，然后弹出 3 和 (6-(2 + 3))*(3 + 8/2)^2 执行加法，然后将 (6-(2 + 3))*(3 + 8/2)^2 + 3 入栈，所以最终结果选 A。

9. 二进制数 101010 和八进制数 166 的和为( )

A. 二进制数 10110000

B. 八进制数 236

C. 十进制数 158

D. 十六进制数 A0

【答案】D

【考点】进制转换

【解析】先将二进制数和八进制数转换成十进制

160 转换成16进制是 A0，八进制是 240，二进制数是 10100000。

10. 假设有一组字符 {a,b,c,d,e,f}，对应的频率分别为 5%，9%，12%，13%，16%，45%。请问以下哪个选项是字符 a, b, c, d, e, f分别对应的一组哈夫曼编码？( )

A. 1111，1110，101，100，110，0

B. 1010，1001，1000，011，010，00

C. 000，001，010，011，10，11

D. 1010，1011，110，111，00，01

【答案】A

【考点】哈夫曼编码/霍夫曼编码

【解析】记住要点: 霍夫曼编码左 0 右 1，哈夫曼编码的形态不唯一，但是 WPL 一定是唯一的，哈夫曼树的形态如下:

哈夫曼树的形态不唯一，但是结点到根节点的路径的长度一定是唯一的，路径的长度是唯一的所以 WPL 是唯一，备考北化刷王道数据结构以前刷到过类似的题目hhh。合并的策略一定是选择 n 个结点中最小的两个结点进行合并，然后再将合并的结果放入合并的集合中。B、C、D 选可以从路径上排除，这个题比较好 👍。

11. 给定一棵二叉树，其前序遍历结果为：ABDECFG，中序遍历结果为：DEBACFG。请问这棵树的正确后序遍历结果是什么？( )

A. EDBGFCA

B. EDGBFCA

C. DEBGFCA

D. DBEGFCA

【答案】A

【考点】树的遍历

【解析】前序遍历顺序: 根左右中序遍历顺序: 左根右

后序遍历: 左右根 ==> EDBGFCA。

12. 考虑一个有向无环图，该图包括4条有向边：(1,2)，(1,3)，(2,4)，和(3,4)。以下哪个选项是这个有向无环图的一个有效的拓扑排序？( )

A. 4，2，3，1

B. 1，2，3，4

C. 1，2，4，3

D. 2，1，3，4

【答案】B

【考点】拓扑排序、有向图

【解析】有向图如下所示

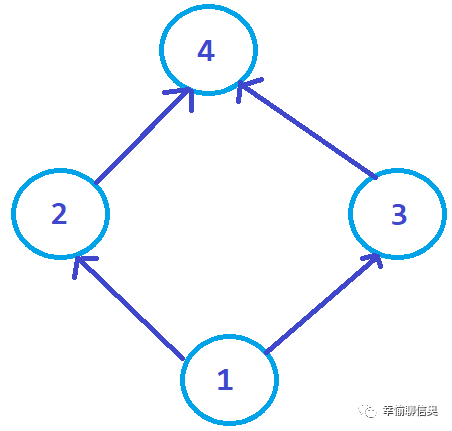
拓扑排序: 度为 0 的点从图中去掉。率先去掉 1 号点，(1,2)，(1,3) 这两条边去掉，度为 0 的点是 2 和 3，可以是 2 这个点先去掉，也可以是 3 这个点去掉，最后去掉 4 这个点，所以拓扑序列是: 1, 2, 3, 4 或者 1, 3, 2, 4。

13. 在计算机中，以下哪个选项描述的数据存储容量最小？( )

A. 字节（byte）

B. 比特（bit）

C. 字（word）

D. 千字节（kilobyte）

【答案】B

【考点】数据存储

【解析】数据存储的基本单位: 字节(Byte)，数据的最小存储单元: 比特(bit)。

1 Byte = 8 bit。

14. 一个班级有10个男生和12个女生。如果要选出一个3人的小组，并且小组中必须至少包含1个女生，那么有多少种可能的组合？（ )

A. 1420

B. 1770

C. 1540

D. 2200

【答案】A

【考点】排列组合

【解析】

① 一个女生，2 个男生

② 两个女生，1 个男生

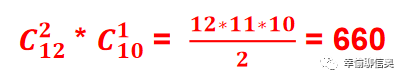
③ 三个女生

最终方案数: 540 + 660 + 220 = 1420。

15. 以下哪个不是操作系统？( )

A. Linux

B. Windows

C. Android

D. HTML

【答案】D

【考点】操作系统

【解析】HTML 前端三剑客之一，超文本标记语言。

第二部分

程序阅读

程序阅读

程序阅读 ①

01 #include<iostream>02 #include<cmath>03 using namespace std;04 05 double f(double a,double b,double c){06     double s=(a+b+c)/2;07     return sqrt(s*(s-a)*(s-b)*(s-c));08 }0910 int main(){11    cout.flags(ios::fixed);12    cout.precision(4);13    14    int a,b,c;15    cin>>a>>b>>c;16    cout<<f(a,b,c)<<endl;17    return 0;18 }

假设输入的所有数都为不超过1000的正整数，完成下面的判断题和单选题：

16. （2分）当输入为“2 2 2”时，输出为“1.7321”( )

【答案】✔

【解析】a = 2, b = 2, c = 2, s = 3, 计算结果如下 👇

17. （2分）将第7行中的"（s-b）*（s-c）"改为"（s-c）*（s-b）"不会影响程序运行的结果( )

【答案】✔

【解析】乘法交换率 = a*b = b*a，所以交换后结果并不会发送变化。

18. （2分）程序总是输出四位小数( )

【答案】✔

【解析】cou.precision(4): 保留四位小数输出。

19. （3分）当输入为“3 4 5”时，输出为( )

A. 6.0000

B. 12.0000

C. 24.0000

D. 30.0000

【答案】A

【解析】a = 3, b = 4, c = 5, s = 6，根据海伦－秦九韶公式知代码求三角形面积，根据 a, b, c 的关系得知是直角三角形，所以面积为 6，故选 A。

20. （3分）当输入为“5 12 13”时，输出为( )

A. 24.0000

B. 30.0000

C. 60.0000

D. 120.0000

【答案】B

【解析】a = 5, b = 12, c = 13，根据海伦－秦九韶公式知代码求三角形面积，根据 a, b, c 的关系得知是直角三角形，所以面积为 30，故选 B。

点评: 第一道题送分题 12 分应该拿满分，语法简单题，未拿到满分的同学应该好好进行自我反思为什么语法难度的阅读题会丢分。

程序阅读 ②

01 #include<iostream>02 #include<vector>03 #include<algorithm>04 using namespace std;05 06 int f(string x,string y){07     int m=x.size();08     int n=y.size();09     vector<vector<int>>v(m+1,vector<int>(n+1,0));10     for(int i=1;i<=m;i++){11         for(int j=1;j<=n;j++){12             if(x[i-1]==y[j-1]){13                 v[i][j]=v[i-1][j-1]+1;14             }else{15                 v[i][j]=max(v[i-1][j],v[i][j-1]);16             }17         }18     }19     return v[m][n];20 }2122 bool g(string x,string y){23     if(x.size() != y.size()){24         return false;25     }26     return f(x+x,y)==y.size();27 }2829 int main(){30     string x,y;31     cin>>x>>y;32     cout<<g(x,y)<<endl;33     return 0;34 }

21. （1.5分）f函数的返回值小于等于min（n,m）。( )

【答案】✔

【解析】f 函数是一个典型的最长公共子序列模型，属于动态规划里面的内容

v[i][j]: 表示字符串 1 前 i 个字符和字符串 2 前 j 个字符，属性值表示共有的子序列，状态转移方程如下 👇

所以 f 函数最终的返回值应该小于等于两个字符串中最小的那个长度。

22. （1.5分） f函数的返回值等于两个输入字符串的最长公共子串的长度。( )

【答案】❌

【解析】子串: 要求连续; 子序列: 要求不连续，f 函数求的是最长公共子序列。

23. （1.5分）当输入两个完全相同的字符串时，g函数的返回值总是true( )

【答案】✔

【解析】f 函数的返回值是字符串的长度，所以 f(x+x, y) = y.size() 是恒成立，所以 g 函数的返回值总是 true。

24. （3分）将第19行中的“v[m][n]”替换为“v[n][m]”，那么该程序( )

A. 行为不变

B. 只会改变输出

C. 一定非正常退出

D. 可能非正常退出

【答案】D

【解析】当字符串 x 和字符串 y 长度相等的情况情况不变，所以排除 B 和 C，当字符串 x 的长度大于或者小于字符串长度 y 导致数组越界访问，可能导致程序异常终止。

25. （3分）当输入为“csp-j p-jcs”时，输出为: ( )

A. 0

B. 1

C. T

D. F

【答案】B

【解析】csp-jcsp-j p-jcs，f 函数的返回值是 5，和 p-jcs 长度相等，g 函数返回 true，bool 类型的输出 true 自动转化成 1。

26. （3分）当输入为“csppsc spsccp”时，输出为: ( )

A. T

B. F

C. 0

D. 1

【答案】D

【解析】csppsccsppsc spsccp，f 函数的返回值是 6，和 spsccp 长度相等，g 函数返回 true，bool 类型的输出 true 自动转化成 1。

点评: 第二道题 f 函数考察同学们对于动态规划学习的检验。

程序阅读 ③

01 #include <iostream>02 #include <cmath>03 using namespace std;04 05 int solve1(int n){06     return n*n;07 }0809 int solve2(int n){10    int sum=0;11    for(int i=1;i<=sqrt(n);i++){12         if(n%i==0){13             if(n/i==i){14                 sum+=i*i;15             }else{16                 sum+=i*i+(n/i)*(n/i);17             }18         }19     }20     return sum;21 }2223 int main(){24     int n;25     cin>>n;26     cout<<solve2(solve1(n))<<" "<<solve1((solve2(n)))<<endl;27     return 0;28 }

27. （1.5分）如果输入的n为正整数，solve2函数的作用是计算n所有的因子的平方和 ( )

【答案】✔

【解析】solve2 函数代码解析如下:

28. （1.5分）第13~14行的作用是避免n的平方根因子i（或n/i）进入第16行而被计算两次 ( )

【答案】✔

【解析】平方数 n 中出现 i 是 n 的因子时，必然 n/i 和 i 相同，同一个因子出现两次但是计算只计算一次，所以该判断题叙述正确。

29. （1.5分）如果输入的n为质数，solve2（n）的返回值为n2+1 ( )

【答案】✔

【解析】循环枚举 i 是从 1 开始枚举，质数的定义除了 1 和它本身外没有其余的因子，所以 sum = n*n + 1*1，所以叙述正确。

30. （4分）如果输入的n为质数 p 的平方，那么 solve2（n）的返回值为( )

A. p2+p+1

B. n2+n+1

C. n2+1

D. P4+2p2+1

【答案】B

【解析】n 的因子有 1, p, n，sum 统计的是 n*n + p*p + 1*1，题目说 n 是质数 p 的平方，那么 p*p = n，等价替换返回值等于 n*n + n + 1 或者 p*p*p*p + p*p + 1，两个答案的变形都算正确，所以最终选 B。

31. （3分）当输入为正整数时，第一项减去第二项的差值一定 ( )

A. 大于0

B. 大于等于0且不一定大于0

C. 小于0

D. 小于等于0且不一定小于0

【答案】D

【解析】特殊代值法排除，当 n 为 1 时 solve2(solve1(n))-solve1((solve2(n)))结果都为 0，因为模拟计算后发现都为 1，所以排除 A、C 两个选项；代入一个值 n为 3 的情况，solve1(3) = 9，solve2(9) = 1*1 + 9*9 + 3*3 = 91，solve2(3) = 1*1 + 3*3 = 10，solve1(10) = 100，91 - 100 = -9，所以选 D，暑期集训说过这种结论题一般代值大概率能找出正确答案，算是做题技巧。

32. （3分）当输入为“5”时，输出为 ( )

A. 651 625

B. 650 729

C. 651 676

D. 652 625

【答案】C

【解析】solve1(5) = 25，solve2(25) = 1*1 + 5*5 + 25*25 = 651。

solve2(5) = 1*1 + 5*5 = 26，solve1(26) = 26*26 = 676。

点评: 数学知识因数分解。

第三部分

程序完善

程序完善

(1)(寻找被移除的元素)问题:原有长度为 n+1 公差为 1 等升数列，将数列输到程序的数组时移除了一个元素，导致长度为 n 的开序数组可能不再连续，除非被移除的是第一个或最后之个元素。需要在数组不连续时，找出被移除的元素。试补全程序。

01 #include <iostream>02 #include <vector>03 04 using namespace std;05 06 int find missing(vector<int>& nums){07    int left = 0, right = nums.size() - 1;08    while (left < right){09        int mid = left + (right  left) / 2;10        if (nums[mid] = mid + ①){11            ②;12        }else{13            ③14        }15    }16    return ④;17 }18 19 int main(){20     int n;21     cin >> n;22     vector<int> nums(n);23     for (int i= 0; i< n; i++) cin >> nums[i];24     int missing_number = find_missing(nums);25     if_(missing_number == ⑤) {26         cout << "Sequence is consecutive" << endl;27     }else{28         cout << "Missing number is " << ,missing numbeer << endl;29     }30     return 0;31 }

二分适用条件: ① 区间单调性 ② 二分的答案满足单调性

单调递增区间查找 >= x 的最小值

int Find_L(int n, int num){ // n 表示 n 个数, num 查询的数     int L = 0, R = n-1; // L:左端点, R:右端点     while(L < R){        int mid = (L+R)>>1; //中间点         if(a[mid] >= num) R = mid; //左子区间         else L = mid + 1; //右子区间     }    return L; //二分的 >= num 的最小值 }

单调递增区间查找 <= x 的最大值

int Find_R(int n, int num){ //n:n个元素,num:查询值     int L = 0, R = n - 1; //L:左端点 R:右端点     while(L < R){         int mid = (L + R + 1)/2; //中间点         if(a[mid] <= num) L = mid; //右区间         else R = mid - 1; //左区间     }    return R; // 二分 <= num 的最大值 }

33. ① 处应填( )

A. 1

B. nums[0]

C. right

D. left

【答案】B

【解析】等差数列公差 1 说明原序列具有连续性，连续必然满足 nums[0] + mid == nums[mid]，不连续 nums[mid] 必然大于 nums[0] + mid。

34. ②处应填( )

A. left=mid+1

B. right=mid-1

C. right=mid

D. left=mid

【答案】A

【解析】当 if 成立说明左区间连续，答案必然在右区间 [mid+1, right] ，通过不断调整左指针 left 和右指针 right 来确定答案处于哪个区间，因此需要将 left 修改成 mid+1。

35. ③处应填( )

A. left=mid+1

B. right=mid-1

C. right=mid

D. left=mid

【答案】C

【解析】if 不成立答案处于左区间 [left, mid]，只需要修改指针 right = mid。

36. ④处应填( )

A. left+nums[0]

B. right+nums[0]

C. mid+nums[0

D. right+1

【答案】A

【解析】返回的是被删除的数，被删除的数即不连续的位置 + 起始值。

37. ⑤处应填( )

A. nums[0]+n

B. nums[0]+n-1

C. nums[0]+n+1

D. nums[n-1]

【答案】D

【解析】如果 n 个数连续， left = right = n-1，返回的数必然是序列中的最后一个数，反之则返回的数即是被删除的数。

这个题大多数认真学的同学都是满分，注意认真学并不是说上课听讲，而是自己课后自己动手去模拟过二分的过程，听老师讲懂了和自己动手验证老师上课讲的内容记忆会更加深刻。

②(编辑距离) 给定两个字符串，每次操作可以选择删除 (Delete)、插入 (Insert)、替换 (Replace)，一个字符，求将第一个字符串转换为第二个字符串所需要的最少操作次数。

1.#include <iostream>2.#include <string>3.#include <vector>4.using namespace std;5. 6.int min(int x,int y,int z){7.    return min(min(x,y),z);8.}9. 10.int edit_dist_dp(string str1,string str2){11.    int m=str1.length();12.    int n=str2.length();13.    vector<vector<int>> dp(m+1,vector<int>(n+1));14. 15.    for(int i=0;i<=m;i++){16.        for(int j=0;j<=n;j++){17.            if(i==0)18.                dp[i][j]= ①;19.            else if(j==0)20.                dp[i][j]= ②;21.            else if(③)22.                dp[i][j]= ④;23.            else24.                dp[i][j]=1+min(dp[i][j-1],min(dp[i-1][j],⑤)); 25.        }26.    }27.    return dp[m][n];28.}29. 30.int main(){31.    string str1,str2;32.    cin>>str1>>str2;33.    cout<<"Mininum number of operation:"34.    <<edit_dist_dp(str1,str2)<<endl;35.    return 0; 36.}