Tarjan算法

Tarjan 算法就是求强连通分量的算法
下面介绍几个定义
强连通图：任意两个定点之间相互可达
强连通分量：非强连通图有向图的极大强连通子图

在Tarjan算法中为每个节点i维护了以下几个变量：
DFN[i]：深度优先搜索遍历时节点i被搜索的次序。
low[i]：节点i能够回溯到的最早位于栈中的节点。
flag[i]：标记i是否在栈中。

这个算法大致过程就是 对于每个节点每条边都要走一遍，当走到原来的已经访问过的节点时，更新low值，并且递归更新该节点的所有父节点的low值，因为我们判断弹出的条件就是当前点的low值等于DFN值，会把栈中这个点及这个点之后的所有节点弹出，然后寻找下一个强连通分量

下面详细介绍一下：
设父节点为v，子节点为u（相对关系）
1.进行深度优先搜索对所有节点搜索
2.此时有两种情况
(1).该节点已经在栈中，也就是已经被访问过，则就要判断节点v的DFN值和节点u的low值的大小来更新节点u的low值。
(2).如果不在栈中，则继续搜索，但是回来的时候不要忘记将u的low值一并更新（与v的low值比较之后再更新）。
上述两种情况一种是根据DFN更新，一种是根据low更新，是有所区别的；
3.回溯完成发现当前low=DFN值时，就可以以当前节点为终点一直弹出节点啦，这就是一个连通分量
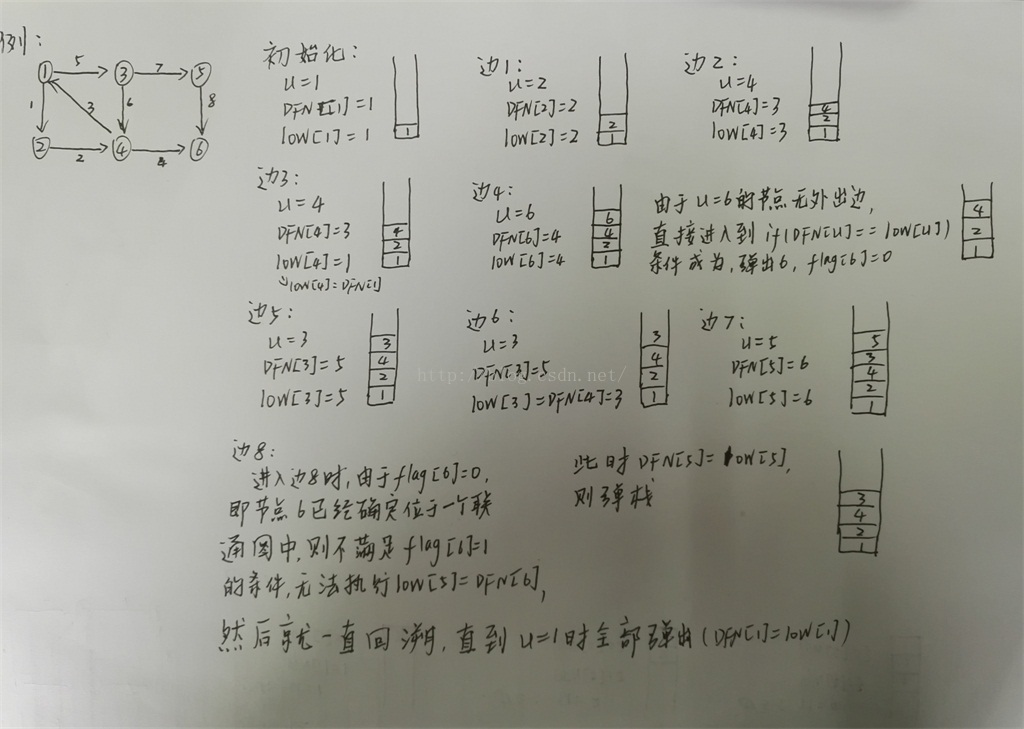
下面附一张大神的图

代码：

#include<iostream>  
using namespace std;  
int DFN[105];                                  //记录在做dfs时节点的搜索次序  
int low[105];                                  //记录节点能够找到的最先访问的祖先的记号  
int count=1;                                   //标记访问次序，时间戳  
int stack[105];                                //压入栈中  
int top=-1;  
int flag[105];                                 //标记节点是否已经在栈中  
int number=0;  
int j;  
int matrix[105][105]={{0,1,1,0,0,0},{0,0,0,1,0,0},{0,0,0,1,1,0},{1,0,0,0,0,1},{0,0,0,0,0,1},{0,0,0,0,0,0}};  
int length;                                    //图的长度  
void tarjan(int u){  
        DFN[u]=low[u]=count++;                     //初始化两个值，自己为能找到的最先访问的祖先  
        stack[++top]=u;  
        flag[u]=1;                                 //标记为已经在栈中  

        for(int v=0;v<length;v++){  
        if(matrix[u][v]){  
            if(!DFN[v]){                       //如果点i没有被访问过  
            tarjan(v);                     //递归访问  
            if(low[v]<low[u])  
                low[u]=low[v];             //更新能找的到祖先  
            }  
            else{                              //如果访问过了，并且该点的DFN更小，则  
            if(DFN[v]<low[u]&&flag[v])     //flag[v]这个判断条件很重要，这样可以避免已经确定在其他联通图的v,因为u到v的单向边而影响到u的low  
            low[u]=DFN[v];                 //也就是已经确定了的联通图要剔除掉，剔除的办法就是判断其还在栈中，因为已经确定了的连通图的点  
            }                                  //flag在下面的do while中已经设为0了(即已经从栈中剔除了)  
        }  
        }  

        //往后回溯的时候，如果发现DFN和low相同的节点，就可以把这个节点之后的节点全部弹栈，构成连通图  
        if(DFN[u]==low[u]){  
        number++;                               //记录连通图的数量  
        do{  
            j=stack[top--];                     //依次取出，直到u  
            cout<<j<<" ";  
            flag[j]=0;                          //设置为不在栈中  
        }while(j!=u);  
            cout<<endl;  
        }  
}  
int main(){  

        memset(DFN,0,sizeof(DFN));                  //数据的初始化  
        memset(low,0,sizeof(low));  
        memset(flag,0,sizeof(flag));  

        length=6;  
        tarjan(0);  

        cout<<endl;  
        for(int i=0;i<6;i++){  
        cout<<"DFN["<<i<<"]:"<<DFN[i]<<" low["<<i<<"]:"<<low[i]<<endl;  
       }  
       return 0;  
}