跳跃表skiplist简析

1.简述

跳跃表(skiplist)最初由 William Pugh发表在ACM通讯上的论文《 Skip lists: a probabilistic alternative to balanced trees   》中,作者给出的定义是：跳表是在很多应用中有可能替代平衡树而作为实现方法的一种数据结构。跳跃列表的算法有同平衡树一样的渐进的预期时间边界，并且更简单、更快速和使用更少的空间。其实，跳表，顾名思义，跳跃的链表，跳表在链表的基础上增加了前向指针，对于链表而言，顺序查找的时间复杂度为线性时间，为了提高查找的效率，在有序链表的节点上增加额外的前向指针，可以通过额外的前向指针跨越链表中的若干个节点，那么到这里问题就来了，当然不是挖掘机哪家强啦。如何知道有序链表需要增加额外的前向指针，要增加多少额外的前向指针以及要跨越的节点数，在跳表的实现中，采用了随机化的技术，使得跳表的查找，插入，删除的平均时间复杂度为O（logn）

以下是一个跳跃表的例图(来自维基百科)：

 

从图中可以看出跳跃表主要有以下几个部分构成：

<1> 表头head：负责维护跳跃表的节点指针

<2> 节点node：实际保存元素值，每个节点有一层或多层

<3> 层level：保存着指向该层下一个节点的指针

<4> 表尾tail：全部由null组成

跳跃表的遍历总是从高层开始，然后随着元素值范围的缩小，慢慢降低到低层。

2.跳表的基本原理

首先考虑有序链表如下，对于查找有序链表中的元素，只能用顺序查找的方法，在线性空间存储的有序元素中，折半查找的方法的时间复杂度为 o(logn) ， 跳表其实采用空间换时间的方法加速查找插入删除这些操作，跳表的性质如下

<1> 由很多层布局构成，level是经由过程必然的概率随机产生的
<2> 每一层都是一个有序的链表，默认是升序
<3> 最底层（Level 1）的链表包含所有元素。
<4> 若是一个元素呈如今Level i 的链表中，则它在Level i 之下的链表也都邑呈现。
<5> 每个节点包含两个指针，一个指向同一链表中的下一个元素，一个指向下面一层的元素

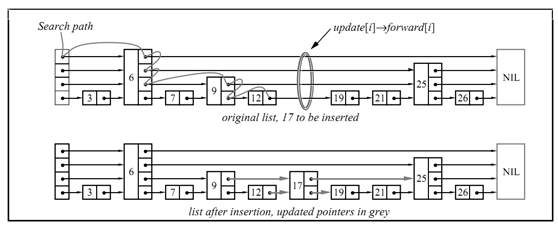
下图列出了从有序链表转化为跳表的过程

3.跳表的实现

跳表作为基础的数据结构在一些开源的实现中使用非常广泛，包括leveldb，redis，都使用跳表作为基础的数据结构。redis中的有序集合就是基于跳表的基础结构实现的，leveldb中的memtable的实现就是基于跳表实现的  .在性能上，跳表完全可以比拟平衡树。 二叉树可以用来表示字典和有序链表等抽象数据结构，当以随机顺序插入元素时，它们表现出非常好，但是连续插入有序元素时，会迅速退化导致非常糟糕的性能。 跳表的表达比树更加直观，算法实现更加简单，比平衡树提供了常量因子速度提升，有效的空间效率，每个节点并不需要存储平衡或优先级信息

跳跃表的查找，插入和删除示意图如下

 

设定跳表的最大层数，每个节点的层数实现根据随机化算法实现，层越高，概率越小

跳表的search实现

跳表的insert实现

跳表的delete实现

参考：

Redis设计与实现

Skip lists: a probabilistic alternative to balanced trees

维基百科-跳跃表