网络流——最大流增广路算法

网络流——最大流增广路算法

---

最大流问题

最大流问题是给定源点 s 和汇点 t ，在允许从其他点中转的情况下，询问最多有多少个物品能从源点 s 运送到汇点 t 。

---

增广路算法

首先提出残量这个概念，残量指的是对应边上容量与流量之差，通俗来说就是这条边再允许通过的最大物品个数

增广路的思想就是找到一条由起点到汇点的路径（这个路径就是增广路），去除这条路径上残量的最大值 delta，为路径上的所有边的流量加上 delta。通俗来说就是有 delta 个物品通过这条路由源点运送到了汇点，而选择运送 delta 件物品的原因显而易见。

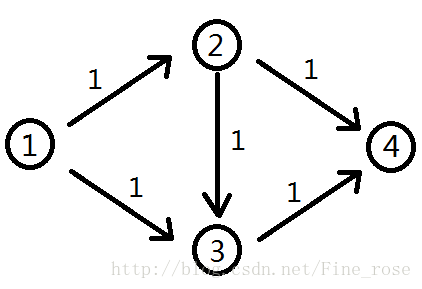
思考下面这种情况

如果我们第一次找 1 - 2 - 3 这条增广路， 通过这条路径我们运送了 1 件物品。如果通过这个增广路运送物品，则我们能够得到的最大值是1。然而答案应是 2 ，方法则是分别通过 1 - 2 - 4 和 1 - 3 - 4 这两条路径。

增广路的思想正确性是显而易见的，但是相对于这个图来说，我们缺少的是一个撤销的操作。如果举出增广路的同时回溯，那复杂度将会上升到指数级别，复杂度无法接受，因此引入了一个反向边的概念。

一条边的反向边就是从它的终点指向它的起点的边，这些反向边同样也具有流量，但是这些流量初始是0。反向边是相对的。

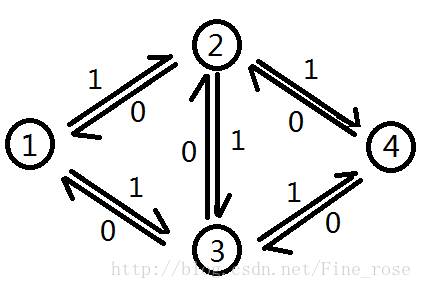
如果加上了反向边，那么图一就会变成如下情况

在图二的情况下，我们同样先从 1 - 2 - 3 - 4 的这条增广路开始，在将增广路上所有边的残量减一的同时，也要对每条边的反向边加一

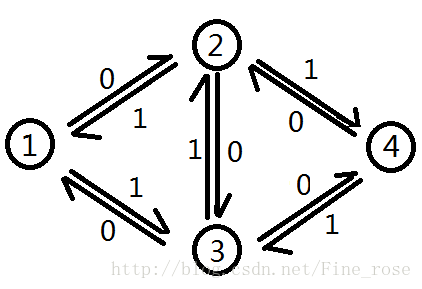
就构成了下图这种情况

这时我们发现 1 - 3 - 2 - 4这条增广路又联通了。注意在走这条增广路的同时也要对对应的反向边操作。

添加反向边的原因是什么呢。其实如果我们走 3 - 2 这条反向边，就会为其对应的 2 - 3 这条刚开始走的边恢复到了 1 ，相当于不经过 2 - 3 这条路径。

这就是增广路算法