优先队列<堆>

1.模型
两个基本操作：
Insert等价Enqueue
DeleteMin删除最小者–Dequeue
2.简单的实现
（1）简单链表–遍历删除Min或者排序删除Min
(2)使用二叉查找树。
反复除去Min会使得树不平衡，并且BST还支持许多不需要的操作。
3.二叉堆
优先队列的实现普遍使用二叉堆，堆有两个性质–结构性和堆序性，对堆的一次操作可能破坏两个性质中的一个，因此堆的操作必须要到堆的性质都被满足时才能终止。
（1）结构性质：堆是一棵除了底层，完全填满的二叉树，底层的元素从左到右填入。–完全二叉树

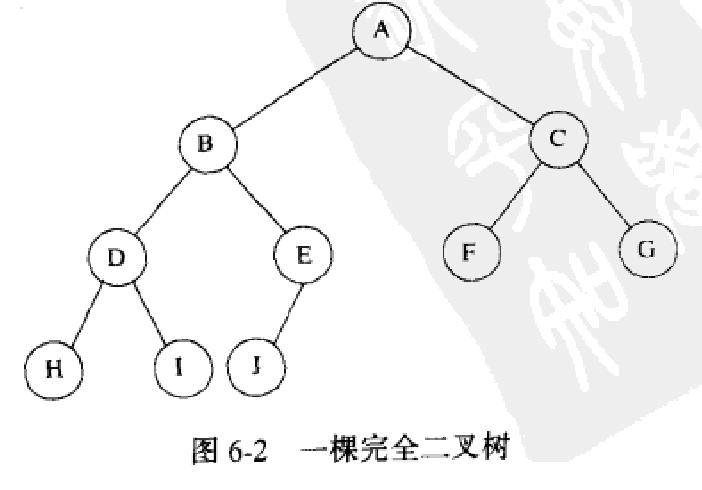
存储：数组存储，对位置i，其左儿子在2*i上，右儿子在2*i+1 上，父亲则在位置floor(i/2)上。

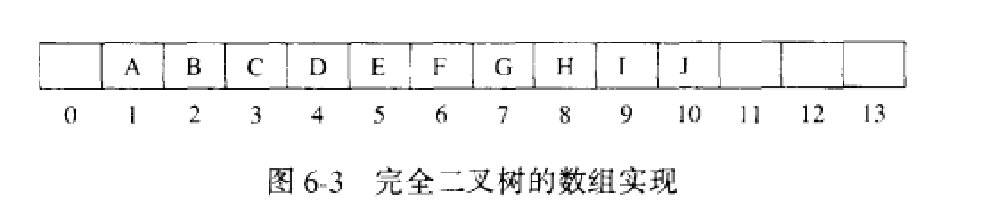
数据结构：数组，代表最大容量的整数以及当前堆大小组成。
（2）堆序性质：在一个堆中，对于每一个节点X，X的父亲中的关键字小于等于X中的关键字，根节点是最小元素.–最小堆
反之，大于等于–最大堆
因此优先队列可以用来找出和删除最小元或者最大元，这需要提前决定。本节讨论最小堆。
（3）基本操作：
插入–上滤
位置0放置一个很小的值，称为标记，使用这种哑信息避免了每个循环都要执行一次的测试，从而节省了一些时间。
删除最小元–下滤
将X置入沿着从根开始包含最小儿子的一条路径上的一个正确位置。
（4)其他操作：
问题：按照最小堆设计的数据结构在求最大元方面却无任何帮助，实际上对任何特定的关键字查找都是没有帮助的（除了线性查找）.
如果我们知道每个元素的具体位置,那么下面几个操作的开销将会变小–
操作：
降低关键字的值DecreaseKey(P,x,H)–上滤
增加关键字的值IncreaseKey(P,x,H)–下滤
删除Delete(P,H)–执行DecreaseKey(P,无穷，H)–执行–DeleteMin(H)
构建堆BuildHeap(H)–N个相继的insert操作
或者直接读入一个数组，执行上滤操作

定理
包含2^（b+1） - 1 个节点高为b的理想二叉树的节点的高度和为2^(b+1)-1-(b+1)
证明–乘公比错位相减法。
4.优先队列的应用
（1）选择问题
未排序的数组中大小为第K个的元素的值
算法a:将N个元素读入一个数组，然后对数组应用BuildHeap算法,执行K次DeleteMin操作，从该堆最后提取的元素就是答案。
如果K=N执行此算法并在元素离开堆的时候记录它们的值，那么我们实际上已经对输入文件以时间O(N logN)作了排序–堆排序
算法b：前K个元素通过调用一次BuildHeap以O(K)被置入堆中，其余的元素中如果有比堆中Max小的就DeleteMax(H),然后Insert之.中位数的时间界是NlogN.最后返回FindMax.–最大堆
(2)事件模拟–银行排队问题等等
5.d-堆
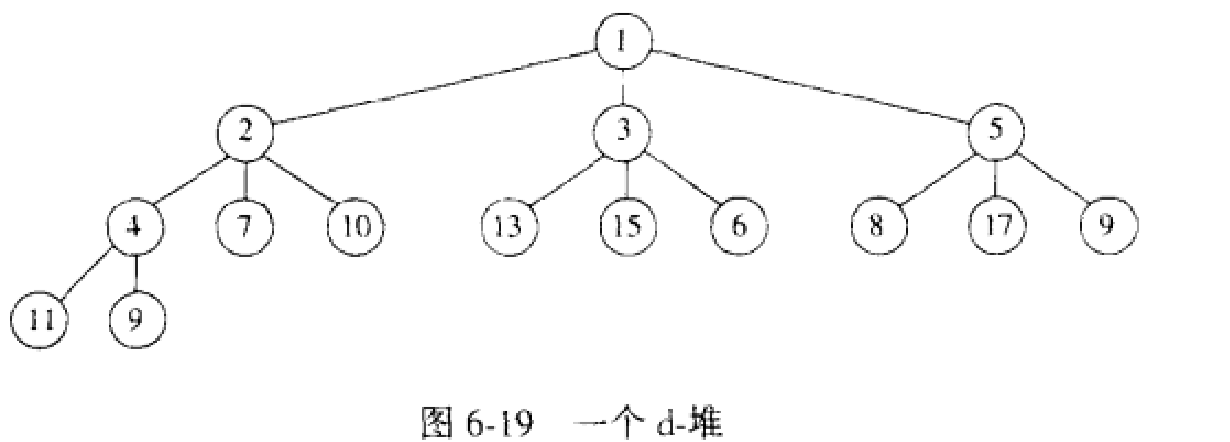
(1) 二叉堆的推广，只是所有的节点都有d个儿子。
(2) 当优先队列太大不能完全装入主存的时候，d-堆能够以B-树大致相同的方式发挥作用，并且实践中4-堆可以胜过二叉堆。
(3)堆的缺点：
a.不能执行Find
b.将两个堆合并成一个堆是困难的操作–合并Merge,但是许多实现堆的方法使得Merge操作的运行时间是O(Log N)

6.左式堆
任一 节点X的零路径长Npl(X)定义为从X到一个没有两个儿子的节点的最短路径的长。因此具有一个或者零个儿子的节点的Npl为0，而Npl(NULL)=-1.

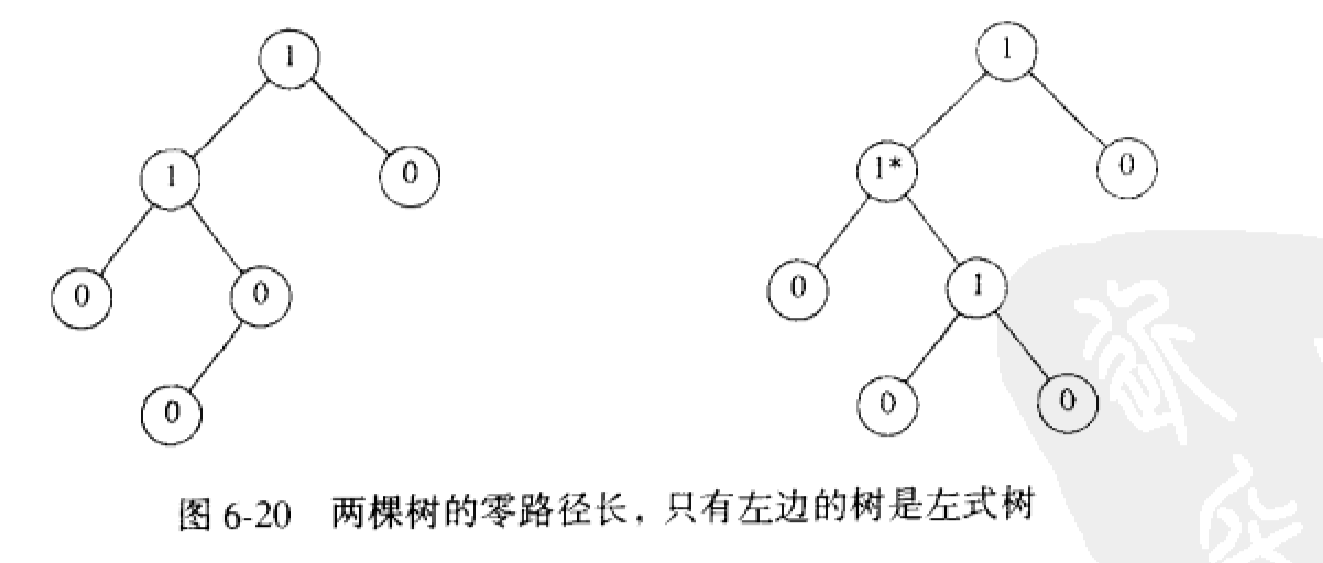
(1)左式堆和二叉树唯一的区别是：左式堆不是理想平衡的，而实际上是趋于非常不平衡.
(2)性质：
a.任一节点的零路径长都比它的诸儿子节点的零路径长的最小值多1。
b.对于堆中的每一个节点X，左儿子的零路径长至少和右儿子的零路径长一样大，故不平衡，更偏重于使树向左增加深度，但便于合并操作。沿左式堆的右路径确实是堆中最短的路径.
(3)定理：
在右路径上有r个节点的左式堆必然至少有2^r -1个节点。

N个节点的左式堆有一条右路径最多含有floor(log(n+1))个节点，对左式堆操作的思路一般是将所有的工作放到右路径上进行，它保证树身短。
7.斜堆
（1）左式堆的自调节形式，斜堆是具有堆序的二叉树，但是不存在对树的结构限制。不同于左式堆，关于任意节点的零路径长的任何信息都不保留，斜堆的右路径在任意时刻都可以任意长，因此所有操作的最坏情形的运行时间均为O(N)，但可以证明任意M次连续操作，总的最坏情形运行时间是O(MlogN),因此斜堆每次操作的摊还时间为O(logN).这点与伸展树类似.
(2)合并操作:对于左式堆，我们查看是否左儿子和右儿子满足左式堆堆序的性质，并交换那些不满足该性质者，但对于斜堆，除了这些右路径上所有节点的最大者不交换它们的左右儿子，交换是无条件的.
(3)优点：不需要附加的空间来保留路径长度以及不需要测试确定何时交换儿子.
8.二项队列
（1）二项队列不是一棵堆序的树，而是堆序的树的集合，称为森林，堆序树中的每一棵都是有约束的形式，叫做二项树。每一个高度上至多存在一棵二项树，高度为0的二项树是一棵单节点树，高度为k的二项树Bk通过将一棵二项树Bk-1附接到另一棵二项树Bk-1的根上而构成.

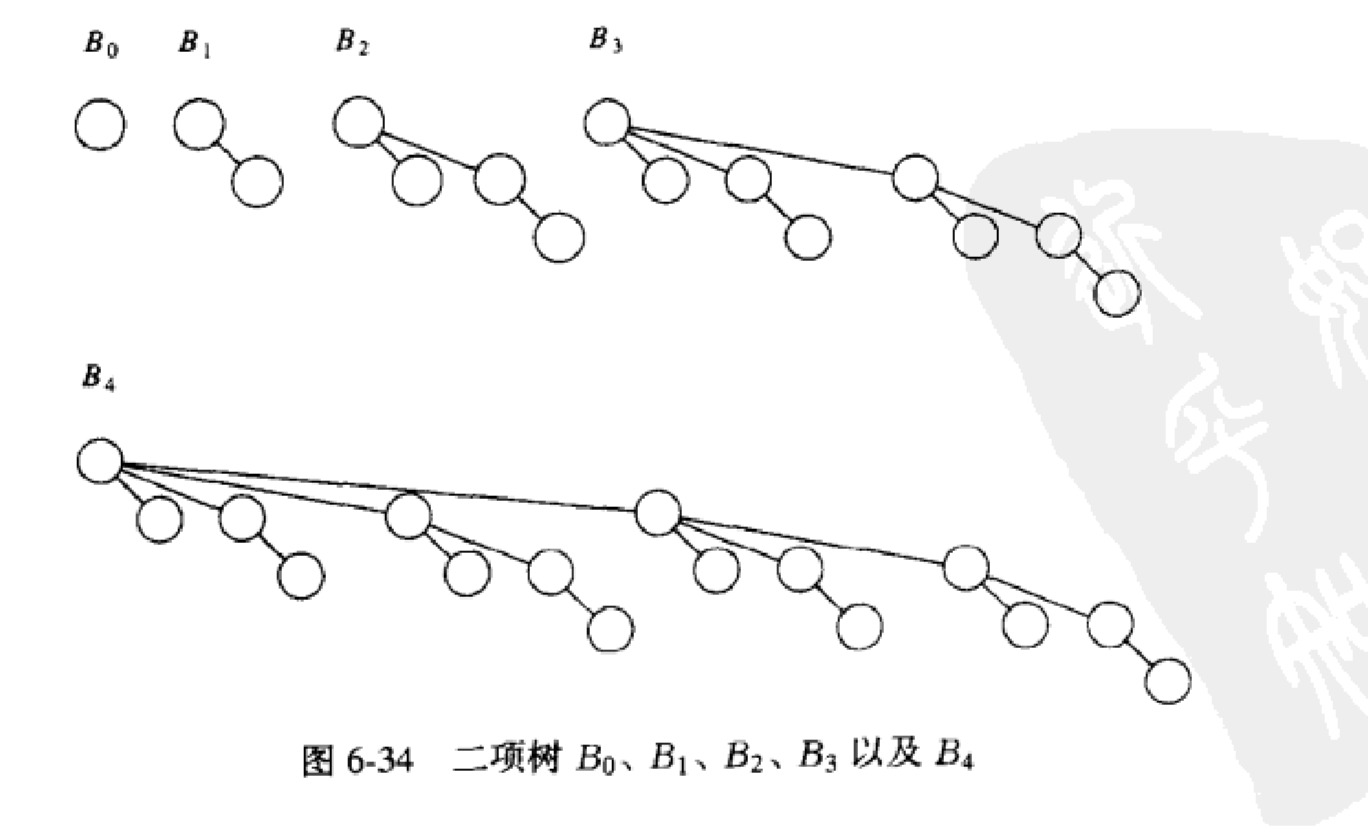
二项树Bk由一个带有儿子B0,B1,……Bk-1的根组成，高度为k的二项树恰有2^k个节点，而在深度d处的节点数是二项系数（k,d)，如果我们把堆序施加到二项树上并允许任意高度上最多有一棵二项树，那么我们能够用二项树的集合唯一的表示任意大小的优先队列.
（2）操作
a.FinMin:最小元可以通过搜索所有的树的根来找出，由于最多有LogN棵不同的树，因此最小元可以时间O(LogN)找到.
b.合并操作：通过将两个队列加到一起来完成–类似二进制的加法运算一样.

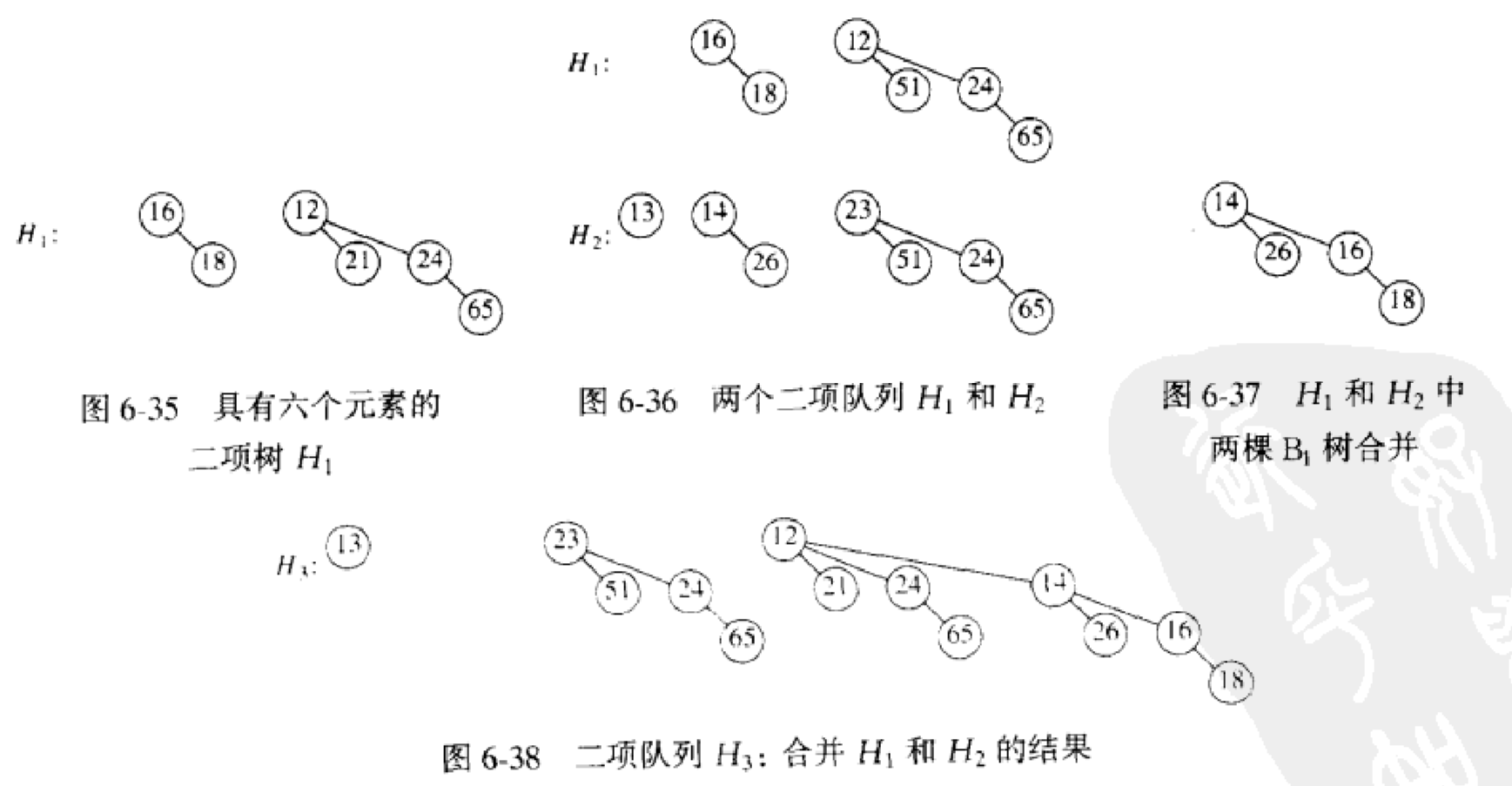
加一次花费常数时间，总共LogN棵二项树，因此合并在最坏情形下花费时间O(LogN).如果将这些树放到按照高度排序的二项队列中,该操作会更加高效.
c.插入–创建一个单节点树并执行一次合并

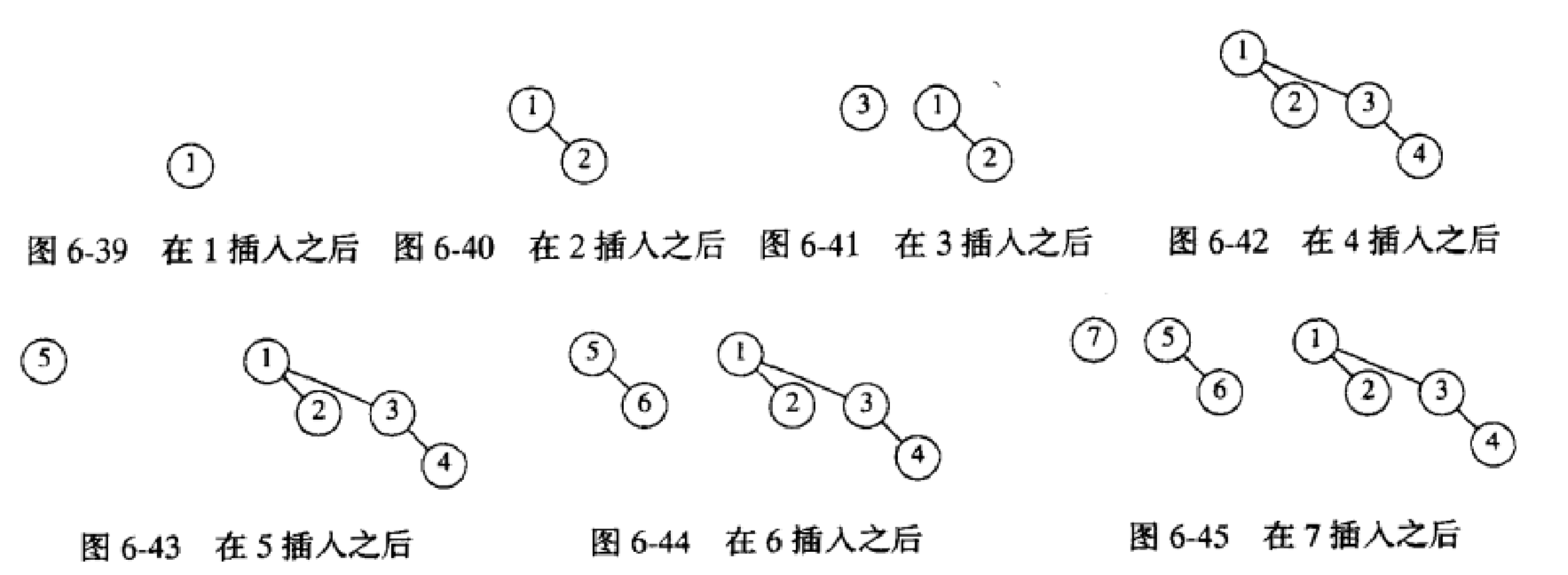
d.DeleteMin

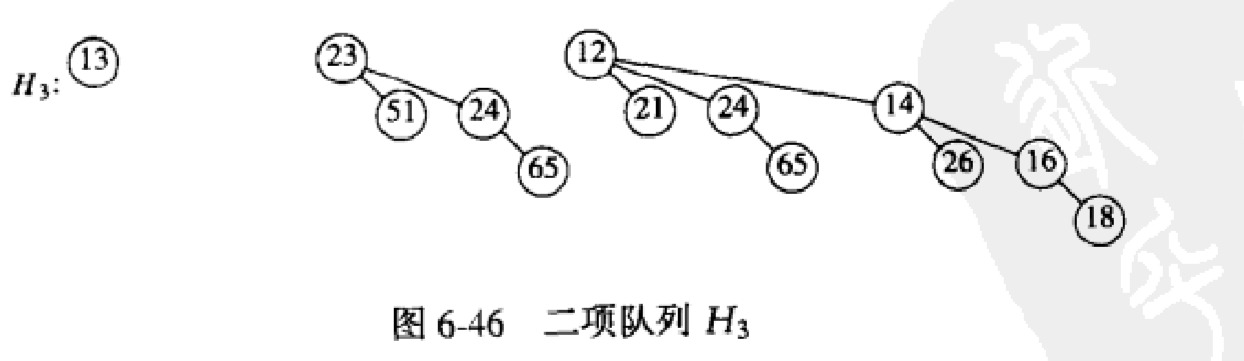
先执行：

然后合并：

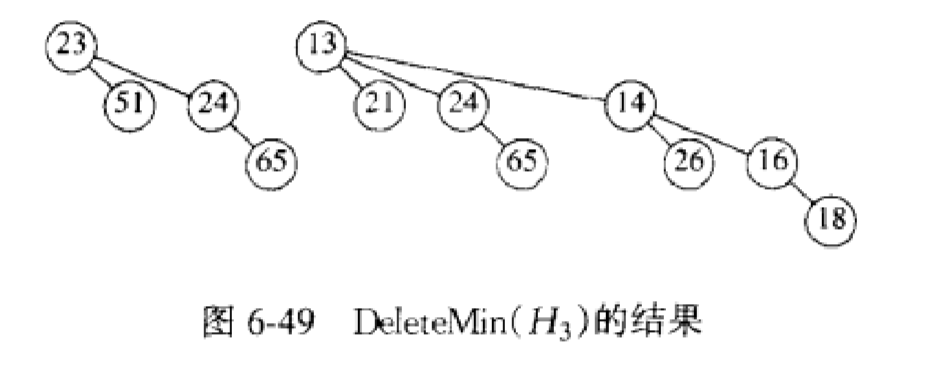
（3）存储
二项树的每一个节点将包含数据，第一个儿子以及右兄弟.且二项树中的诸儿子以递减次序排列.

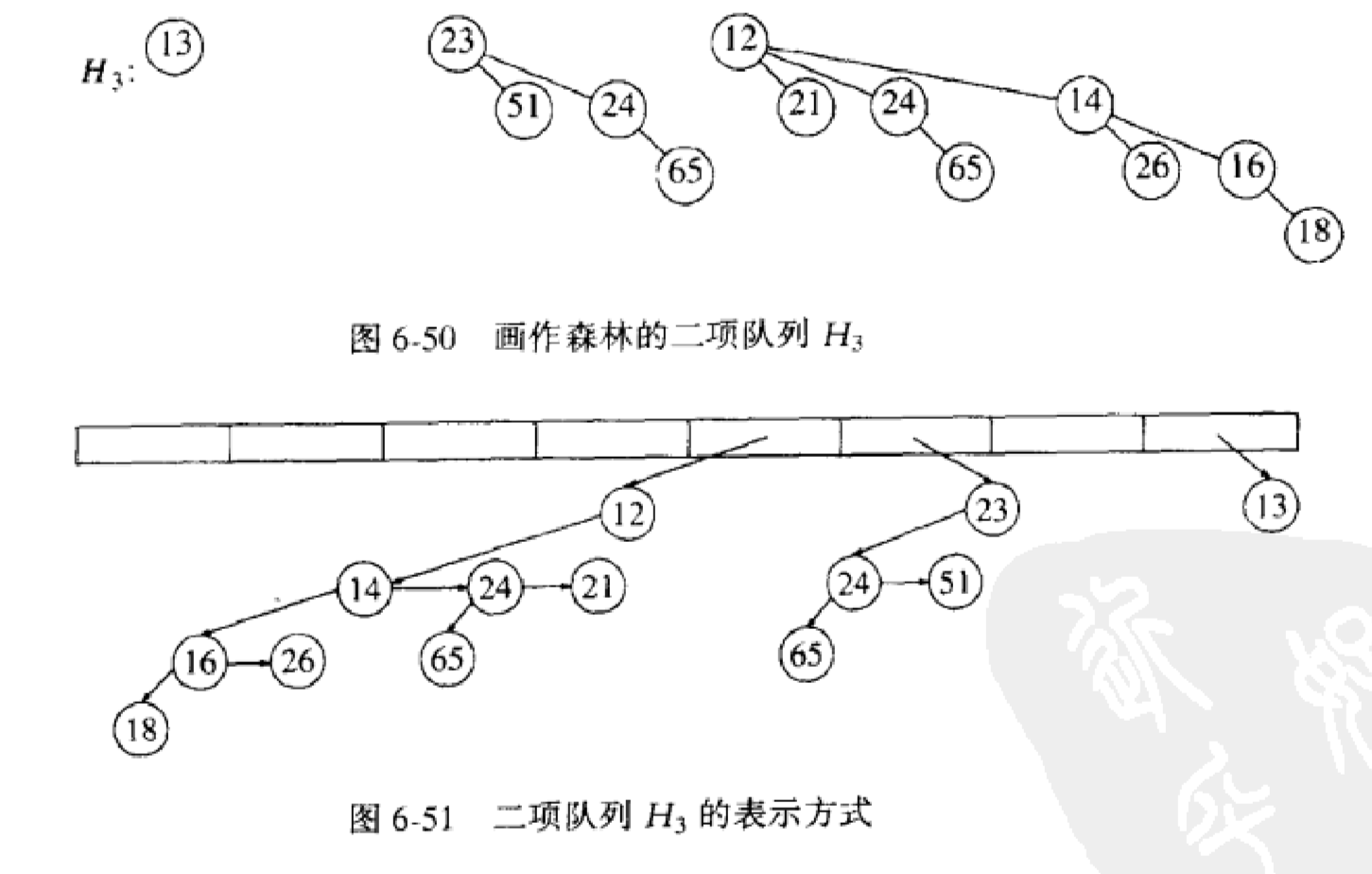
注意：
树的秩：树节点容量的度量,B+树中每个节点包含目录项的个数m需满足d≤m≤2d，根节点是1≤m≤2d。其中d为树的秩
总结
优先队列
（1）二叉堆
（2）左式堆–递归
（3）斜堆–缺少平衡原则
（4）二项队列
应用：操作系统的工作调度到模拟