层次分析法——评价类

层次分析法

模型引出

问题的提出

日常生活中有很多的决策问题。决策是指在面临多种方案时需要依据一定的标准选择某一种方案。
买衣服，一般要依据质量、颜色、价格、款式等方面的因素选择；旅游，是去风光秀丽的苏州，还是去迷人的北戴河，或者是去山水甲天下的桂林，那一般会依据景色、费用、食宿条件、旅途等因素来判断去哪个地方。

现在微博要选出一个明星作为微博之星，现在有三个候选明星A、B、C，该选择哪位明星呢？
考虑一个明星的成就可以看其粉丝数、颜值、作品数量、作品质量(考虑用作品某瓣平均评分代替)
A、B、C的相关数据如下

明星	粉丝数	颜值	作品质量	作品数量
A	6000w	10	6.5	25
B	3400w	6	8.1	46
C	5500w	8	7.5	31

怎么能让指标在同一数量级，且保证在同一指标下其差距不变？

首先进行归一化处理（把数划到0到1之间）：指标的数组[a b c]归一化处理得到[a/(a+b+c), b/(a+b+c), c/(a+b+c)]

步骤

1、建立的递阶层次结构模型

2、构造出各层次中的所有判断矩阵

构造出各层次中的所有判断矩阵
• 对指标的重要性进行两两比较，构造判断矩阵，从而科学求出权重
• 矩阵中元素aij的意义是，第𝑖个指标相对第𝑗个指标的重要程度

因两两比较的过程中忽略了其他因素，导致最后的结果可能出现矛盾

​ 如上表可以看出𝑎23 =1/2代表在重要性上，颜值不如作品质量； 𝑎24 =2代表着颜值比作品数量重要，因此可以看出作品质量比作品数量重要，但𝑎34= 1/2意味着作品质量不如作品数量重要，与上一条矛盾！
所以需要一致性检验!

3、一致性检验

一致性检验就是来看看判断矩阵中的各个指标重要程度是否一致。

矩阵的秩：秩就是经过我们初等行变化，化到最简之后，我们数不为0行数有几行。因为一致矩阵的各行各列都成比例，所以我们一定能化到只有一行，即秩一定为1。

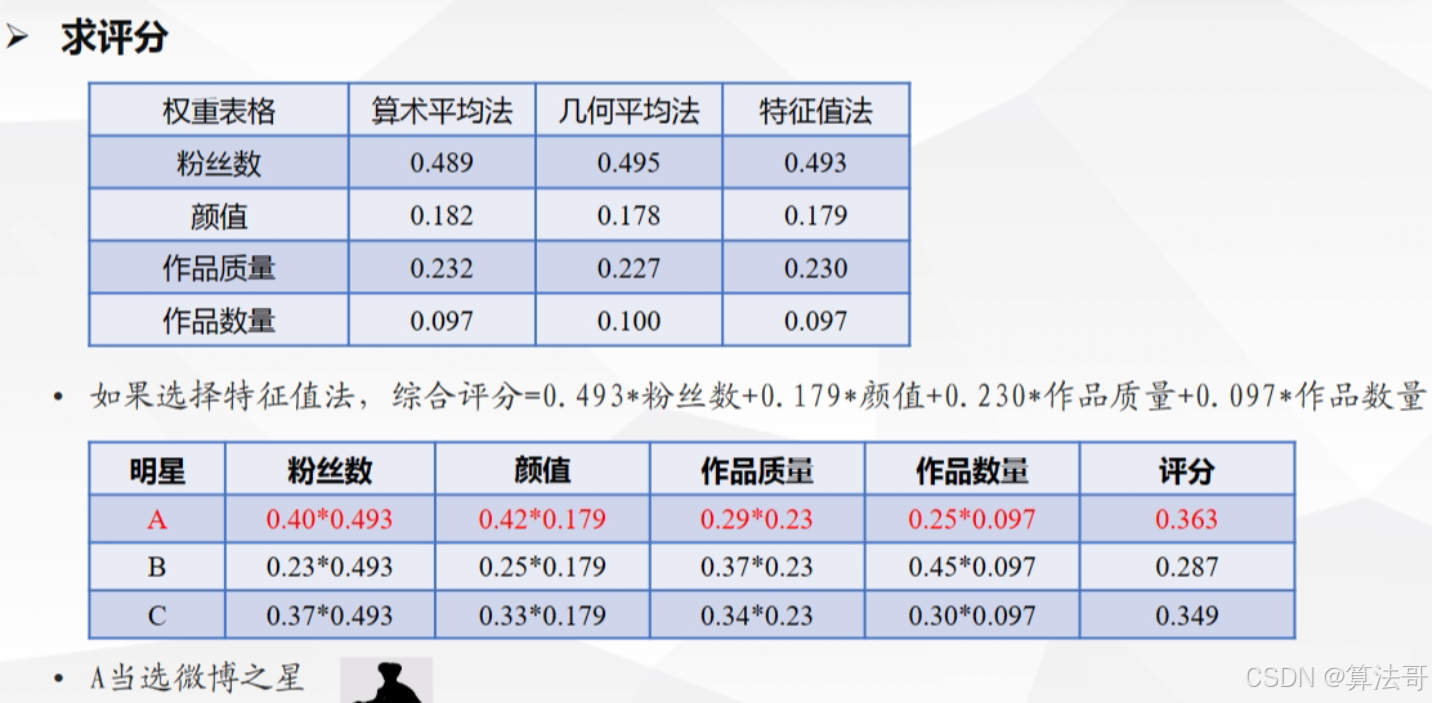
4、求出权重后进行评价

有下列三种方法求权重：

层次分析法代码：

一致性检验代码

A = input('判断矩阵A='); %输入判断矩阵
[n,n] = size(A); %获取A的行和列
%求出最大特征值以及对应的特征向量
[V,D] = eig(A); %V是特征向量 D是特征值构成的对角矩阵
Max_eig = max(max(D)); %先求出每一列的最大值，再求最大值中的最大值
CI = (Max_eig - n) / (n-1);
RI=[0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
%注意哦，这里的RI最多支持 n = 15
%这里n=2时，一定是一致矩阵，所以CI = 0，我们为了避免分母为0，将这里的第二个元素改为了很接近0的正数
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
disp('因为CR<0.10，所以该判断矩阵A的一致性可以接受!');
else
disp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
end

求权重代码

%------------------------------算术平均法求权重-----------------------------------
A = input('判断矩阵A='); %输入判断矩阵
ASum = sum(A,1); %将判断矩阵每列求和
[n,n] = size(A); %获取A的行和列，用于对ASum复制，对应位相除归一化
Ar = repmat(ASum,n,1); %复制Asum n行1列为Ar矩阵
Stand_A = A./Ar; %归一化
ASumr = sum(Stand_A,2); %各列相加到同一行
disp(ASumr/n); %将相加后得到的向量每个元素除以n可以得到权重向量

%------------------------------几何平均法求权重-----------------------------------
clc;
A = input('判断矩阵A=‘); %输入判断矩阵
[n,n] = size(A); %获取A的行和列
prod_A = prod(A,2); %将A中每一行元素相乘得到一列向量
prod_n_A = prod_A.^(1/n); %将新的向量的每个分量开n次方等价求1/n次方
re_prod_A = prod_n_A./sum(prod_n_A);%归一化处理
disp(re_prod_A); %展示权重结果

%------------------------------特征值法计算权重-----------------------------------
clc;
A = input('判断矩阵A=‘); %输入判断矩阵
[n,n] = size(A); %获取A的行和列
%求出最大特征值以及对应的特征向量
[V,D] = eig(A); %V是特征向量 D是特征值构成的对角矩阵
Max_eig = max(max(D)); %先求出每一列的最大值，再求最大值中的最大值
[r,c] = find(Max_eig == D,1);%使用find()函数找出最大特征值对应的特征向量
%对特征向量进行归一化得到所需权重
disp(V(:,c)./sum(V(:,c)));