【数据结构与算法学习笔记-Tree】_删除t的第i棵子树-CSDN博客

本文链接：https://blog.csdn.net/floating_heart/article/details/123993867

本文为学习笔记，感兴趣的读者可在MOOC中搜索《数据结构与算法Python版》或阅读《数据结构（C语言版）》（严蔚敏）
目录链接：https://blog.csdn.net/floating_heart/article/details/123991211

2.1 树Tree

2.1.1 什么是树Tree

树(Tree)是以分支关系定义的层次结构，是n(n>=0)个结点组成的有限集。

在这里插入图片描述

树的特点如下：

分类体系是层次化的。

树是一种分层结构越接近顶部的层越普遍
越接近底部的层越独特
一个节点的子节点与另一个节点的子节点相互之间是隔离、独立的。
每一个叶节点都具有唯一性。

以动物分类为例子，可以用从根开始到达每个种的完全路径来唯一标识每个物种
动物界->脊索门->哺乳纲->食肉目->猫科->猫属->家猫种
Animalia->Chordate->Mammal->Carnivora->Felidae->Felis->Domestica

树在各个领域中被广泛应用：

树结构在客观世界中广泛存在，如人类社会的族谱和各种社会组织机构都可用树来形象表示。

树在计算机领域中也得到广泛应用，包括操作系统、图形学、数据库系统、计算机科学等

例如文件系统、HTML文档（嵌套标记）、域名体系
如编译程序中，可以用树来表示源程序的语法结构
如数据库中的树形结构

对树的结构和操作的研究，有利于我们对上述内容的理解。

2.1.2 树结构的相关术语

节点（Node）：

节点是树中的元素，是组成树的基本部分。每个节点具有名称，或"键值"，节点还可以保存额外数据项，数据项根据不同的应用而变。

度（Degree）：节点拥有的子树数称为节点的度。

边（Edge）：边是组成树的另一个基本部分

每条边恰好连接两个节点，表示节点之间具有关联，边具有出入方向；
每个节点（除根节点）恰有一条来自另一节点的入边；
每个节点可以有多条连到其它节点的出边。

根（Root）：树中唯一一个没有入边的节点

路径（Path）：由边依次连接在一起的节点的有序列表

如：HTML->BODY->UL->LI，是一条路径

子节点（Children）：入边均来自于同一个节点的若干节点，称为这个节点的子节点

父节点（Parent）：一个节点是其所有出边所连接节点的父节点

兄弟节点（Sibling）：具有同一个父节点的节点之间称为兄弟节点

子树（Subtree）：一个节点和其所有子孙节点，以及相关边的集合

叶节点（Leaf）：没有子节点的节点称为叶节点

层级（Level）：从根节点开始到达一个节点的路径，所包含的边的数量，称为这个节点的层级。

如D的层级为2，根节点的层级为0

高度：树中所有节点的最大层级称为树的高度

如下图树的高度为2

结合这些术语，定义树的方式有两种：

第一种：普通定义

在陈斌的课程中，树的一般定义如下：

树由若干节点，以及两两连接节点的边组成，并有如下性质：
其中一个节点被设定为根；
每个节点n(除根节点)，都恰连接一条来自节点p的边，p是n的父节点；
每个节点从根开始的路径是唯一的，如果每个节点最多有两个子节点，这样的树称为“二叉树”

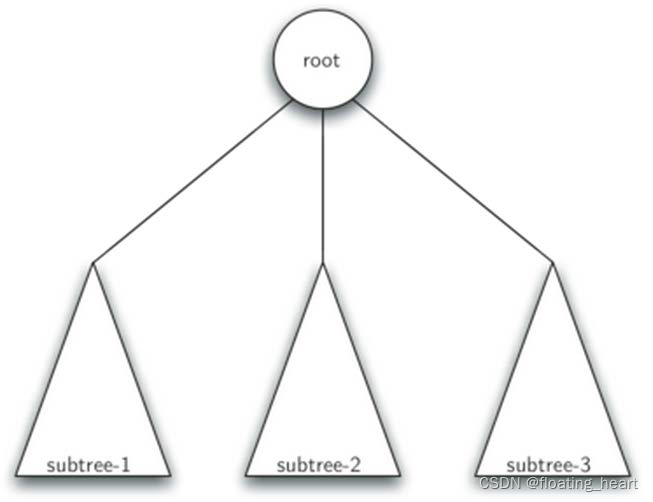
第二种：递归定义（树本身是一种可以递归的结构）

在陈斌的课程中，树的递归定义如下：

树是：
空集；
或者由根节点及0或多个子树构成（其中子树也是树），每个子树的根到根节点具有边相连。

在这里插入图片描述

在严蔚敏．数据结构（C语言版）,2007中，对树的结构定义如下：

下面先给出严蔚敏．数据结构（C语言版）,2007中对抽象数据类型Tree的定义

ADT Tree{
	数据对象D: D是具有相同特性的数据元素的集合。
	数据关系R: 若D为空集，则称为空树；
		若D仅含一个数据元素，则R为空集，否则R = {H}，H是如下二元关系：
		(1)在D中存在唯一的称为根的数据元素root，它在关系H下无前驱；
		(2)若D-{root}≠Φ，则存在D-{root}的一个划分D1,D2,...,Dm(m>0)，对任意j≠k(1≤j,k≤m)有Dj∩Dk = Φ，且对任意的i(1≤i≤m)，唯一存在数据元素xi∈Di，有<root, xi>∈H；
		(3)对应于D-{root}的划分，H-{<root,xi>,...,<root,xm>}有唯一的一个划分H1,H2,...,Hm(m>0)，对任意j≠k(1≤j,k≤m)有Hj∩Hk=Φ，且对任意i(1≤i≤m)，Hi是Di上的二元关系，(Di,{Hi})是一棵符合本定义的树，称为根root的子树。
	基本操作P：
		InitTree(&T):
			操作结果：构造空树T。
		DestroyTree(&T):
			初始条件：树T存在。
			操作结果：销毁树T。
		CreateTree(&T,definition):
			初始条件：definition给出树T的定义。
			操作结果：按definition构造树T。
		ClearTree(&T):
			初始条件：树T存在。
			操作结果：将树T清为空树。
		TreeEmpty(T):
			初始条件：树T存在。
			操作结果：若T为空树，则返回TRUE，否则FALSE。
		TreeDepth(T):
			初始条件：树T存在。
			操作结果：返回T的深度。
		Root(T):
			初始条件：树T存在。
			操作结果：返回T的根。
		Value(T,cur_e):
			初始条件：树T存在，cur_e是T中某个节点。
			操作结果：返回cur_e的值。
		Assign(T,cur_e,value):
			初始条件：树T存在，cur_e是T中某个节点。
			操作结果：节点cur_e赋值为value。
		Parent(T,cur_e):
			初始条件：树T存在，cur_e是T中某个节点。
			操作结果：若cur_e是T的非根节点，则返回它的双亲，否则函数值为“空”。
		LeftChild(T,cur_e):
			初始条件：树T存在，cur_e是T中某个节点。
			操作结果：若cur_e是T的非叶子节点，则返回它的最左孩子，否则返回“空”。
		RightSibling(T,cur_e):
			初始条件：树T存在，cur_e是T中某个节点。
			操作结果：若cur_e有右兄弟，则返回它的右兄弟，否则函数值为“空”。
		InsertChild(&T,&p,i,c):
			初始条件：树T存在，p指向T中某个节点，1≤i≤p所指节点的度+1，非空树c与T不相交。
			操作结果：插入c为T中p指节点的第i棵子树。
		DeleteChild(&T,&p,i):
			初始条件：树T存在,p指向T中某个节点，1≤i≤p指节点的度。
			操作结果：删除T中p所指节点的第i棵子树。
		TraverseTree(T,Visit()):
			初始条件：树T存在,Visit是对节点操作的应用函数。
			操作结果：按某种次序对T的每个节点调用函数visit()一次且至多一次。一旦visit()失败，则操作失败。
}ADT Tree

之后我们仅对部分功能进行实现，来检验我们对树相关操作的理解。

2.1.3 树的简单实现：嵌套列表

我们尝试分别用Python List和JavaScript Array来实现二叉树的数据结构。

采用递归的嵌套列表构建二叉树，通过具有三个元素的列表来实现。

第一个元素为根节点的值

第二个元素是左子树（同样是一个列表）

第三个元素是右子树（同样是一个列表）

[ root, left, right ]

嵌套列表的优点在于：

子树的结构与树相同，是一种递归数据结构。
很容易扩展到多叉树，仅需要增加列表元素即可。

定义的基本操作：

BinaryTree：创建仅有根节点的二叉树
insertLeft/insertRight：将新节点插入树中作为其直接的左/右子节点
get/setRootVal：则取得或返回根节点
getLeft/RightChild：返回左/右子树

代码：Python

def BinaryTree(r):
  return [r,[],[]]

def insertLeft(root,newBranch):
  t = root.pop(1)
  root.insert(1,[newBranch,t,[]])
  return root

def insertRight(root,newBranch):
  t = root.pop(2)
  root.insert(2,[newBranch,[],t])
  return root

def getRootVal(root):
  return root[0]

def setRootVal(root,newVal):
  root[0] = newVal

def getLeftChild(root):
  return root[1]

def getRightChild(root):
  return root[2]

# r = BinaryTree(3)
# insertLeft(r,4)
# insertLeft(r,5)
# insertRight(r,6)
# insertRight(r,7)
# l = getLeftChild(r)
# print(l)
# print(r)

代码：JavaScript

function BinaryTree(r) {
  return [r, [], []]
}

function insertLeft(root, newBranch) {
  let t = root.splice(1, 1)[0]
  root.splice(1, 0, [newBranch, t, []])
  return root
}

function insertRight(root, newBranch) {
  let t = root.splice(2, 1)[0]
  root.splice(2, 0, [newBranch, [], t])
  return root
}

function getRootVal(root) {
  return root[0]
}

function setRootVal(root, newVal) {
  root[0] = newVal
}

function getLeftChild(root) {
  return root[1]
}

function getRightChild(root) {
  return root[2]
}
/*
let r = BinaryTree(3)
insertLeft(r, 4)
insertLeft(r, 5)
insertRight(r, 6)
insertRight(r, 7)
let l = getLeftChild(r)
console.log(l)
console.log(r)*/

2.1.4 树的简单实现：链表

与之前无序表和有序表类似，树同样可以通过链表来实现。

链表中每个节点保存根节点的数据项，以及指向左右子树的链接，如图所示。

定义的基本操作与嵌套列表法一致，此处不再重复，实现过程也较为简单，代码如下

代码：Python

class BinaryTree:
  def __init__(self,rootObj) -> None:
    self.key = rootObj
    self.leftChild = None
    self.rightChild = None

  def insertLeft(self,newNode):
    t = BinaryTree(newNode)
    t.leftChild = self.leftChild
    self.leftChild = t
  def insertRight(self,newNode):
    t = BinaryTree(newNode)
    t.rightChild = self.rightChild
    self.rightChild = t
  
  def getRightChild(self):
    return self.rightChild
  
  def getLeftChild(self):
    return self.leftChild
  
  def setRootVal(self,obj):
    self.key = obj
  
  def getRootVal(self):
    return self.key

# r = BinaryTree('a')
# r.insertLeft('b')
# r.insertRight('c')
# r.getRightChild().setRootVal('hello')
# r.getLeftChild().insertRight('d')

代码：JavaScript

class BinaryTree {
  constructor(rootObj) {
    this.key = rootObj
    this.leftChild = null
    this.rightChild = null
  }

  insertLeft(newNode) {
    let t = new BinaryTree(newNode)
    t.leftChild = this.leftChild
    this.leftChild = t
  }
  insertRight(newNode) {
    let t = new BinaryTree(newNode)
    t.rightChild = this.rightChild
    this.rightChild = t
  }

  getRightChild() {
    return this.rightChild
  }
  getLeftChild() {
    return this.leftChild
  }

  setRootVal(obj) {
    this.key = obj
  }
  getRootVal() {
    return this.key
  }
}

let r = new BinaryTree('a')
r.insertLeft('b')
r.insertRight('c')
r.getRightChild().setRootVal('hello')
r.getLeftChild().insertRight('d')
console.log(r)

2.1.5 树的应用示例：表达式解析

树可以应用在各个方面，于此我们通过表达式解析这一简单的例子增进对树的理解。

应用描述：

在这一应用中，我们将表达式表示为树结构：
叶节点保存操作数，内部节点保存操作符；

根据计算的优先级划分树的层级，越低层的节点，优先级越高；

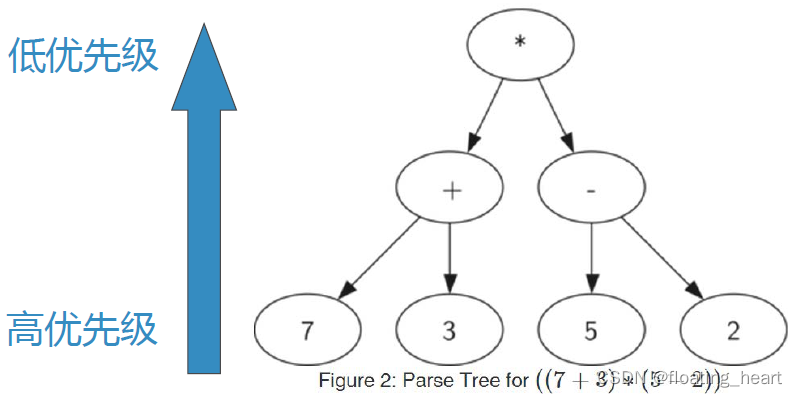
树中每一个子树都表示一个子表达式。将子树替换为子表达式值的节点，即可实现求值。

于此，我们进行的尝试如下：

从全括号表达式构建表达式解析树；
利用表达式解析树对表达式求值；
从表达式解析树生成全括号表达式。

步骤一：全括号表达式->表达式解析树

算法说明：

以(3+(4*5))为例：

分解为单词表[‘(’, ‘3’, ‘+’, ‘(’, ‘4’, ‘*’, ‘5’,‘)’, ‘)’]
创建表达式解析树
1. 创建空树，当前节点为根节点
2. 读入’('，创建了左子节点，当前节点下降
3. 读入’3’，当前节点设置为3，上升到父节点
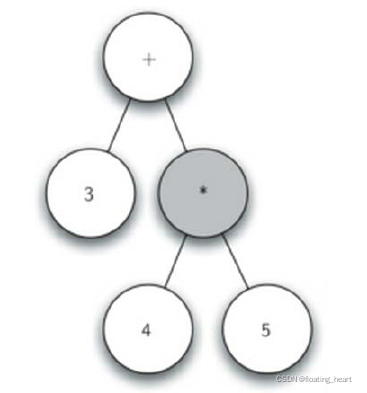
4. 读入’+'，当前节点设置为+，创建右子节点，当前节点下降
5. 读入’('，创建左子节点，当前节点下降
6. 读入’4’，当前节点设置为4，上升到父节点
7. 读入’**'，当前节点设置为*，创建右子节点，当前节点下降
  
  ![]](https://img-blog.csdnimg.cn/9a3557da45a8436ba256c1cecdba763b.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAZmxvYXRpbmdfaGVhcnQ=,size_19,color_FFFFFF,t_70,g_se,x_16)
8. 读入’5’，当前节点设置为5，上升到父节点
9. 读入’)'，上升到父节点
10. 读入’)'，再上升到父节点

代码：Python

# 节点下降采用getChild等方法
# 节点下降过程中采用栈记录路径
# 节点上升通过栈来获得
from BinaryTree import BinaryTree
from Stack import Stack

def buildParseTree(fpexp):
  fplist = fpexp.split()
  pStack = Stack()
  eTree = BinaryTree('')
  pStack.push(eTree)
  currentTree = eTree
  for i in fplist:
    if i == '(':
      currentTree.insertLeft('')
      pStack.push(currentTree)
      currentTree = currentTree.getLeftChild()
    elif i not in ['+','-','*','/',')']:
      currentTree.setRootVal(int(i))
      parent = pStack.pop()
      currentTree = parent
    elif i in ['+','-','*','/']:
      currentTree.setRootVal(i)
      currentTree.insertRight('')
      pStack.push(currentTree)
      currentTree = currentTree.getRightChild()
    elif i == ')':
      currentTree = pStack.pop()
    else:
      raise ValueError
  return eTree

步骤二：表达式解析树求值

算法说明：

由于二叉树是一个递归数据结构，所以采用递归的算法来处理，相关解析如下：

基本结束条件：
叶节点是最简单的子树，没有左右子节点，其根节点的数据项即为子表达式树的值

缩小规模：
将表达式树分为左子树、右子树，即为缩小规模

调用自身：
分别调用evaluate计算左子树和右子树的值，然后将左右子树的值依根节点的操作符进行计算，从而得到表达式的值

代码：Python

import operator

def evaluate(parseTree):
  # 引入operator，调用函数更方便
  opers = {'+':operator.add,'-':operator.sub,\
    '*':operator.mul,'/':operator.truediv}

  leftC = parseTree.getLeftChild()
  rightC = parseTree.getRightChild()

  if leftC and rightC:
    fn = opers[parseTree.getRootVal()]
    return fn(evaluate(leftC),evaluate(rightC))
  else:
    return parseTree.getRootVal()

代码：JavaScript

下面用JavaScript重写代码

import Stack from './Stack_c.js'
import BinaryTree from './BinaryTree.js'

function buildParseTree(fpexp) {
  let fplist = fpexp.split(' ')
  let pStack = new Stack()
  let eTree = new BinaryTree('')

  pStack.push(eTree)
  let currentTree = eTree

  for (let i of fplist) {
    if (i == '(') {
      currentTree.insertLeft('')
      pStack.push(currentTree)
      currentTree = currentTree.getLeftChild()
    } else if (!['+', '-', '*', '/', ')'].includes(i)) {
      currentTree.setRootVal(parseInt(i))
      currentTree = pStack.pop()
    } else if (['+', '-', '*', '/'].includes(i)) {
      currentTree.setRootVal(i)
      currentTree.insertRight('')
      pStack.push(currentTree)
      currentTree = currentTree.getRightChild()
    } else if (i == ')') {
      currentTree = pStack.pop()
    } else {
      throw TypeError
    }
  }
  return eTree
}

function evaluate(parseTree) {
  let leftC = parseTree.getLeftChild()
  let rightC = parseTree.getRightChild()

  if (leftC && rightC) {
    switch (parseTree.getRootVal()) {
      case '+':
        return evaluate(leftC) + evaluate(rightC)
      case '-':
        return evaluate(leftC) - evaluate(rightC)
      case '*':
        return evaluate(leftC) * evaluate(rightC)
      case '/':
        return evaluate(leftC) / evaluate(rightC)
    }
  } else {
    return parseTree.getRootVal()
  }
}
let a = '( ( 1 * 2 ) + 3 )'
console.log(evaluate(buildParseTree(a)))

2.1.6 树的遍历

线性数据结构中，对所有数据项的访问比较简单直接，按照顺序进行即可。

由于树的非线性特点，使遍历操作较为复杂。

树的遍历方法可分为三种：

前序遍历（preorder）：先访问根节点，再递归地前序访问左子树、最后前序访问右子树；
中序遍历（inorder）：先递归地中序访问左子树，再访问根节点，最后中序访问右子树；
后序遍历（postorder）：先递归地后序访问左子树，再后序访问右子树，最后访问根节点。

代码：Python

# 前序遍历
def preorder(tree):
  if tree:
    print(tree.getRootVal())
    preorder(tree.getLeftChild())
    preorder(tree.getRightChild())

# 中序遍历
def inorder(tree):
  if tree:
    inorder(tree.getLeftChild())
    print(tree.getRootVal())
    inorder(tree.getRightChild())

# 后序遍历
def postorder(tree):
  if tree:
    postorder(tree.getLeftChild())
    postorder(tree.getRightChild())
    print(tree.getRootVal())

代码：JavaScript

// 前序遍历
function preorder(tree){
  if (tree){
    console.log(tree.getRootVal())
    preorder(tree.getLeftChild())
    preorder(tree.getRightChild())
  }
}

// 中序遍历
function inorder(tree){
  if (tree){
    inorder(tree.getLeftChild())
    console.log(tree.getRootVal())
    inorder(tree.getRightChild())
  }
}

// 后序遍历
function preorder(tree){
  if (tree){
    preorder(tree.getLeftChild())
    preorder(tree.getRightChild())
    console.log(tree.getRootVal())
  }
}

在BinaryTree中添加遍历方法

代码：Python

  # 添加遍历方法
  # 前序遍历
  def preorder(self):
    print(self.key)
    if self.leftChild:
      self.leftChild.preorder()
    if self.rightChild:
      self.rightChild.preorder()

  # 中序遍历
  def inorder(self):
    if self.leftChild:
      self.leftChild.preorder()
    print(self.key)
    if self.rightChild:
      self.rightChild.preorder()

  # 后序遍历
  def postorder(self):
    if self.leftChild:
      self.leftChild.preorder()
    if self.rightChild:
      self.rightChild.preorder()
    print(self.key)

代码：JavaScript

  // 添加遍历方法
  // 前序遍历
  preorder() {
    console.log(this.key)
    if (this.leftChild) {
      preorder(this.leftChild)
    }
    if (this.rightChild) {
      preorder(this.rightChild)
    }
  }
  // 中序遍历
  inorder() {
    if (this.leftChild) {
      preorder(this.leftChild)
    }
    console.log(this.key)
    if (this.rightChild) {
      preorder(this.rightChild)
    }
  }
  // 后序遍历
  preorder() {
    if (this.leftChild) {
      preorder(this.leftChild)
    }
    if (this.rightChild) {
      preorder(this.rightChild)
    }
    console.log(this.key)
  }

步骤二：表达式解析树求值-后序遍历（第二种递归形式）

上一种步骤二的解决方案把递归调用的内容放在了return的内容中，此处的解决方案与上一种思路一致，只不过调整了递归调用内容的位置。

代码：Python

# 表达式解析树求值-后序遍历
def postordereval(parseTree):
  opers = {'+':operator.add,'-':operator.sub,\
  '*':operator.mul,'/':operator.truediv}

  if parseTree:
    leftC = postordereval(parseTree.getLeftChild())
    rightC = postordereval(parseTree.getRightChild())
    if leftC and rightC:
      return opers[parseTree.getRootVal()](leftC,rightC)
    else:
      return parseTree.getRootVal()

代码：JavaScript

// 表达式解析树求值-后序遍历
function postordereval(parseTree) {
  if (parseTree) {
    let leftC = postordereval(parseTree.getLeftChild())
    let rightC = postordereval(parseTree.getRightChild())

    if (leftC && rightC) {
      switch (parseTree.getRootVal()) {
        case '+':
          return leftC + rightC
        case '-':
          return leftC - rightC
        case '*':
          return leftC * rightC
        case '/':
          return leftC / rightC
      }
    } else {
      return parseTree.getRootVal()
    }
  }
}

步骤三：表达式解析树->全括号表达式 - 中序遍历

采用中序遍历算法生成全括号中缀表达式

代码：Python

# 表达式解析树生成全括号表达式
def printexp(tree):
  sVal = ''
  if tree:
    leftC = printexp(tree.getLeftChild())
    rightC = printexp(tree.getRightChild())
    if leftC != '' and rightC != '':
      sVal = '(' + leftC + str(tree.getRootVal()) + rightC + ')'
    else:
      sVal = str(tree.getRootVal())
  return sVal

代码：JavaScript

// 表达式解析树生成全括号表达式
function printexp(tree) {
  let sVal = ''
  if (tree) {
    let leftC = printexp(tree.getLeftChild())
    let rightC = printexp(tree.getRightChild())
    if (leftC != '' && rightC != '') {
      sVal = '(' + leftC + String(tree.getRootVal()) + rightC + ')'
    } else {
      sVal = String(tree.getRootVal())
    }
  }
  return sVal
}