CSS3中的矩阵

CSS3中的矩阵
CSS3中的矩阵指的是一个方法，书写为matrix()和matrix3d()，前者是元素2D平面的移动变换(transform)，后者则是3D变换。2D变换矩阵为3*3,如下面矩阵示意图；3D变换则是4*4的矩阵。

有些迷糊？恩，我也觉得上面讲述有些不合时宜。那好，我们先看看其他东西，层层渐进——transform属性。

 

transform中有这么几个属性方法：

.trans_skew { transform: skew(35deg); }//元素翻转给定的角度

.trans_scale { transform:scale(1, 0.5); }//元素的尺寸会增加或减少

.trans_rotate { transform:rotate(45deg); }//元素顺时针旋转给定的角度

.trans_translate {transform:translate(10px, 20px); }//素从其当前位置移动

斜拉(skew)，缩放(scale)，旋转(rotate)以及位移(translate)。

 

为什么transform:rotate(45deg);会让元素旋转45°,其后面运作的机理是什么呢？

 

下面这张图可以解释上面的疑问：

 

无论是旋转还是拉伸什么的，本质上都是应用的matrix()方法实现的（修改matrix()方法固定几个值），只是类似于transform:rotate这种表现形式，我们更容易理解，记忆与上手。

 

换句话说，理解transform中matrix()矩阵方法有利于透彻理解CSS3的transform属性.

 

在CSS3以及HTML5的世界里，这玩意还是涉猎蛮广的，如SVG以及canvas.

 

CSS3 transform的matrix()方法写法如下：

transform: matrix(a,b,c,d,e,f);

吓住了吧，这多参数，一个巴掌都数不过来。

实际上，这6参数，对应的矩阵就是：

注意书写方向是竖着的

上面提过，要让其发生变化，只有与另外就可以了，即使这是个小阵。

反应在这里就是如下转换公式：

其中，x, y表示转换元素的所有坐标（变量）了。那后面的ax+cy+e怎么来的呢？

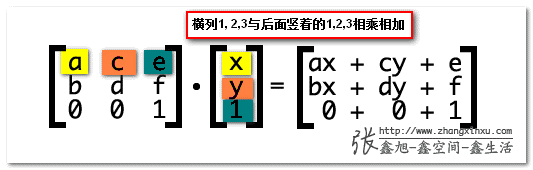
很简单，3*3矩阵每一行的第1个值与后面1*3的第1个值相乘，第2个值与第2个相乘，第3个与第3个，然后相加，如下图同色标注：

那ax+cy+e的意义是什么？
记住了，ax+cy+e为变换后的水平坐标，bx+dy+f表示变换后的垂直位置。

 

假设矩阵参数如下：

transform: matrix(1, 0, 0, 1, 30, 30); /* a=1, b=0, c=0, d=1, e=30, f=30 */

现在，我们根据这个矩阵偏移元素的中心点，假设是(0, 0)，即x=0, y=0。

于是，变换后的x坐标就是ax+cy+e = 1*0+0*0+30 =30, y坐标就是bx+dy+f = 0*0+1*0+30 =30.

于是，中心点坐标从(0, 0)变成了→(30, 30)。好好想象下，原来(0,0)的位置，移到了白点的(30, 30)处，怎么样，是不是往右下方同时偏移了30像素哈！！

实际上transform: matrix(1, 0, 0,1, 30, 30);就等同于transform: translate(30px, 30px);. 注意：translate, rotate等方法都是需要单位的，而matrix方法e, f参数的单位可以省略。

 

总结
聪明的你可能以及意识到了，尼玛matrix表现偏移就是：

transform: matrix(与我无关, 哪位, 怎么不去高考, 打麻将去吧,水平偏移距离, 垂直偏移距离);

 

 

transform matrix矩阵与缩放，旋转以及拉伸

偏移是matrix效果中最简单，最容易理解的，因此，上面很详尽地对此进行展开说明。下面，为了进一步加深对matrix的理解，会简单讲下matrix矩阵与缩放，旋转以及拉伸效果。

缩放(scale)
上面的偏移只要关心最后两个参数，这个缩放也是只要关心两个参数。哪两个呢？

如果你足够明察秋毫，应该已经知道了，因为上面多次出现的：

transform: matrix(1, 0, 0, 1, 30, 30);

已经出卖了。

发现没，matrix(1, 0,0, 1, 30, 30);的元素比例与原来一样，1:1,而这几个参数中，有两个1,啊哈哈！没错，这两个1就是缩放相关的参数。

其中，第一个缩放x轴，第二个缩放y轴。

用公式就很明白了，假设比例是s，则有matrix(s, 0, 0, s, 0, 0);，于是，套用公式，就有：
x' = ax+cy+e = s*x+0*y+0 = s*x;
y' = bx+dy+f = 0*x+s*y+0 = s*y;

 

也就是matrix(sx, 0, 0, sy, 0, 0);，等同于scale(sx,sy);

 

 

旋转(rotate)
旋转相比前面两个要更高级些，要用到（可能勾起学生时代阴影的）三角函数。

Cosθ   -sinθ  0 Sinθ   cosθ   0 0      0      1

方法以及参数使用如下（假设角度为θ）：

matrix(cosθ,sinθ,-sinθ,cosθ,0,0)

结合矩阵公式，就有：

 

不过，说句老实话，就旋转而言，rotate(θdeg)这种书写形式要比matrix简单多了，首先记忆简单，其次，无需计算。例如，旋转30°，前者直接：

transform:rotate(30deg);

而使用matrix表示则还要计算cos, sin值：

transform: matrix(0.866025,0.500000,-0.500000,0.866025,0,0);

拉伸(skew)
拉伸也用到了三角函数，不过是tanθ，而且，其至于b, c两个参数相关，书写如下（注意y轴倾斜角度在前）：

matrix(1,tan(θy),tan(θx),1,0,0)

套用矩阵公式计算结果为：

x' = x+y*tan(θx)+0 = x+y*tan(θx) 

y' = x*tan(θy)+y+0 = x*tan(θy)+y

对应于skew(θx +"deg"，θy+ "deg")这种写法。

其中，θx表示x轴倾斜的角度，θy表示y轴，两者并无关联。

 

我想有人会奇怪，既然CSS3 transform中提供了像skew, rotate, …效果，那还需要掌握和熟悉让人头大的矩阵方法干嘛呢？

好问题，确实，对于一般地交互应用，transform属性默认提供的些方法是足够了，但是，一些其他的效果，如果transform属性没有提供接口方法，那你又该怎么办呢？

 

没辙了吧，这是，就只能靠matrix矩阵了。要知道，matrix矩阵是transform变换的基础，可以应付很多高端的效果，算是一种高级应用技巧吧。掌握了基础，才能兵来将挡水来土掩啊。