法线矩阵
在很多顶点shader中都用到了gl_NormalMatrix。这里将介绍这个矩阵是什么,以及它的作用。
大部分计算是在视图空间内完成的,主要原因是光照的运算要放在这个空间内,否则一些依赖观察点坐标的效果,比如镜面反射光就很难实现。
所以我们需要将法线变换到视图空间。变换一个顶点到视图空间的方法如下:
下面的代码很简单地实现了这个要求:
让我们看看潜在的问题:
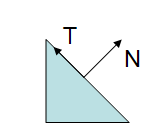
在上图中我们可以看到一个三角面以及它的法线和切线。下图显示了如果模型视图矩阵包含非一致缩放(non-uniform scale)的话会发生什么。
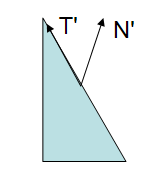
注意,如果缩放是一致的(uniform),那么法线方向保持不变,变的只是长度,而且可以通过归一化修正这个影响。
在上图中,模型视图矩阵应用到所有顶点以及法线上,最后的结果明显错误:法线不再与三角面垂直了。
现在我们知道模型视图矩阵在某些情况下,不能用来变换法线向量。下面的问题就是:那么该使用哪个矩阵?
考虑一个3×3矩阵G,让我们看看要正确变换法线,这个矩阵该是什么样子。
我们知道,变换前切线和法线是垂直的,即T•N = 0,在变换后切线和法线同样应该保持垂直,即T’•N’ = 0。现在假设G是正确变换法线的矩阵,同时模型视图矩阵的左上3×3子矩阵M可以正确变换切线T(T是一个向量,所以w成分为0)。因为T可以通过两个顶点的差来计算,所以变换顶点的矩阵同样可以用来变换T。由此可以得到如下等式:

向量的点乘相当于向量的内积,所以有:
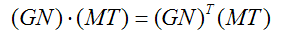
我们知道相乘的转置等于分别转置再交换顺序相乘:
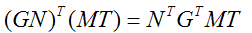
已知N和T点乘结果为0,所以如果下式成立就可以满足等式为0:
即有:

可见变换法线的正确矩阵是M的逆的转置。OpenGL计算出的这个矩阵就保存在gl_NormalMatrix里。
在本节开始讨论过,某些情况下使用模型视图矩阵也可以。当模型视图矩阵的左上3×3子矩阵M正交时,可以得到:
一个正交矩阵的所有行/列都为单位向量,并且互相正交。当两个向量乘上正交矩阵时,它们之间的夹角在变换前后不变。由于这种保角变换的关系,所以法线和切线依然保存垂直。此外,向量的长度也保持不变。
M在什么时候能确定为正交的呢?当我们把几何变换限制为旋转和平移时(在OpenGL应用程序中只使用glRotate和glTranslate,而不使用glScale),就可以保证M正交。注意:gluLookAt同样建立正交矩阵。
关于法线归一化
当一个法线到达顶点shader后,我们一般会将它归一化:
我们可以避免归一化计算吗?在某些情况下是可行的。如果gl_NormalMatrix是正交矩阵,那么经过变换后输入法线的长度不会变,依然等于gl_Normal。所以如果在OpenGL程序中法线已经是归一化的,那么在shader中就不需要在重复了。
也就是说,如果我们使用gluLookAt设置照相机,对模型值进行旋转和平移变换,就可以在shader中避免使用归一化操作。这对于归一化过的光线向量也是适用的。
片断shader的情况
在片断shader中,我们经常发现需要重新归一化在顶点shader中归一化的法线。这是必要的吗?答案是肯定的。
考虑一个包含三个不同顶点法线的三角面。片断shader接收经过插值的法线,插值基于距离三个顶点的远近。这样得到的法线方向是对的,但不再是单位长度了。
下图显示了原因。图中黑线表示三角面,顶点法线用蓝色表示,插值得到的片断法线用绿色表示。所有的插值法线排列在黑色的点划线上。从图上可以看出绿色的插值法线大小小于单位长度的顶点法线。

注意,如果顶点法线没有单位化,那么得到的插值法线的方向也将是错误的。所以,即使一个顶点没有在顶点shader用到,也可能要对它在顶点shader中进行归一化。
有一种情况,在片断shader中可以避免归一化操作,那就是每个顶点法线方向相同,而且顶点法线是经过归一化的。此时顶点法线插值得到的结果都相同。
以方向光为例,每个片断都需要考虑光线方向,如果光线向量已经在之前归一化了,在片断shader中就可以避免归一化这一步。
在很多顶点shader中都用到了gl_NormalMatrix。这里将介绍这个矩阵是什么,以及它的作用。
大部分计算是在视图空间内完成的,主要原因是光照的运算要放在这个空间内,否则一些依赖观察点坐标的效果,比如镜面反射光就很难实现。
所以我们需要将法线变换到视图空间。变换一个顶点到视图空间的方法如下:
- vertexEyeSpace = gl_ModelViewMatrix * gl_Vertex;
vertexEyeSpace = gl_ModelViewMatrix * gl_Vertex;下面的代码很简单地实现了这个要求:
- normalEyeSpace = vec3(gl_ModelViewMatrix * vec4(gl_Normal,0.0));
normalEyeSpace = vec3(gl_ModelViewMatrix * vec4(gl_Normal,0.0));让我们看看潜在的问题:


在上图中,模型视图矩阵应用到所有顶点以及法线上,最后的结果明显错误:法线不再与三角面垂直了。
现在我们知道模型视图矩阵在某些情况下,不能用来变换法线向量。下面的问题就是:那么该使用哪个矩阵?
考虑一个3×3矩阵G,让我们看看要正确变换法线,这个矩阵该是什么样子。
我们知道,变换前切线和法线是垂直的,即T•N = 0,在变换后切线和法线同样应该保持垂直,即T’•N’ = 0。现在假设G是正确变换法线的矩阵,同时模型视图矩阵的左上3×3子矩阵M可以正确变换切线T(T是一个向量,所以w成分为0)。因为T可以通过两个顶点的差来计算,所以变换顶点的矩阵同样可以用来变换T。由此可以得到如下等式:

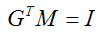

在本节开始讨论过,某些情况下使用模型视图矩阵也可以。当模型视图矩阵的左上3×3子矩阵M正交时,可以得到:
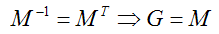
M在什么时候能确定为正交的呢?当我们把几何变换限制为旋转和平移时(在OpenGL应用程序中只使用glRotate和glTranslate,而不使用glScale),就可以保证M正交。注意:gluLookAt同样建立正交矩阵。
关于法线归一化
当一个法线到达顶点shader后,我们一般会将它归一化:
- normal = normalize(gl_NormalMatrix * gl_Normal);
normal = normalize(gl_NormalMatrix * gl_Normal);我们可以避免归一化计算吗?在某些情况下是可行的。如果gl_NormalMatrix是正交矩阵,那么经过变换后输入法线的长度不会变,依然等于gl_Normal。所以如果在OpenGL程序中法线已经是归一化的,那么在shader中就不需要在重复了。
也就是说,如果我们使用gluLookAt设置照相机,对模型值进行旋转和平移变换,就可以在shader中避免使用归一化操作。这对于归一化过的光线向量也是适用的。
片断shader的情况
在片断shader中,我们经常发现需要重新归一化在顶点shader中归一化的法线。这是必要的吗?答案是肯定的。
考虑一个包含三个不同顶点法线的三角面。片断shader接收经过插值的法线,插值基于距离三个顶点的远近。这样得到的法线方向是对的,但不再是单位长度了。
下图显示了原因。图中黑线表示三角面,顶点法线用蓝色表示,插值得到的片断法线用绿色表示。所有的插值法线排列在黑色的点划线上。从图上可以看出绿色的插值法线大小小于单位长度的顶点法线。

有一种情况,在片断shader中可以避免归一化操作,那就是每个顶点法线方向相同,而且顶点法线是经过归一化的。此时顶点法线插值得到的结果都相同。
以方向光为例,每个片断都需要考虑光线方向,如果光线向量已经在之前归一化了,在片断shader中就可以避免归一化这一步。























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








