EM 算法通俗简明详细系统介绍

1）EM 算法之目的 一种通过迭代的期望最大化算法（Expectation-Maximization Algorithm）
\qquad 通过观察数据，获取模型参数。例如 $x_1,x_2,...,x_n$，为某班男女同学身高，其中，男生身高服从高斯分布1：${\mathrm{N}}_1({\mu }_1,{\sigma }_1)$；女生身高服从高斯分布2：${\mathrm{N}}_2({\mu }_2,{\sigma }_2)$；没有其他性别。求：男女分布的参数${\mu }_1,{\sigma }_1,{\mu }_2,{\sigma }_2$)

2）EM 算法之难点
\qquad 不知道谁是男是女。。。。。
\qquad 不知道男女比例。。。。。
有隐变量(记为:z)在问题中，有点不好搞。

3）EM 算法之通用说明

符号说明：
观察值 X：$x_1,x_2,...,x_n$
分布参数 $\theta$ ： 含各类分布参数
隐变量z：例如上例中的男女
概率$p(X|\theta )$：在$\theta$已知条件下，$x_1,x_2,...,x_n$ 出现的概率，极大似然的目标函数。
概率$p(X|z,\theta )$：在z，$\theta$已知条件下，X 出现的概率， 这货好算，相当于知道了是男娃子还是女娃子。
概率$p(X,z|\theta )$：在$\theta$已知条件下，同时X和z的概率。这货嘛，如果知道了男女娃子的先验概率，也好算。由于男同学概率+女同学概率=1.0，所以有： ${\sum }_{z}p(X,z|\theta )=p(X|\theta )$，z被积掉了。

4）EM 算法之三个基础知识

• 贝叶斯公式： $P(A|B)=\frac{P(A)P(B|A)}{P(B)}$, 不说了，好懂的。

• 极大似然估计法： $l(\theta )=p(X|\theta )$ = ${\prod }_{i=1}^{n}p(x_i|\theta )$

  实际中常用对数最大似然：$lnl(\theta )$=${\sum }_{i=1}^{n}lnp(x_i|\theta )$

  即： $\hat{\theta }=\underset{\theta }{\mathrm{argmax}}{\sum }_{i=1}^{n}ln(p(x_i|\theta ))$，相乘变成相加。
  例如：只有一种高斯分布时，化简易得：
  $lnl(\theta )$=${\sum }_{i=1}^n[-ln\sqrt{2\pi }-\frac{1}{2}ln{\sigma }^2-\frac{(x_i-\mu {)}^2}{2{\sigma }^2}]$
  $\frac{\partial lnl(\theta )}{\partial u}=0=>\hat{\mu }=\frac{x_1+x_2+...+x_n}{n}$
  $\frac{\partial lnl(\theta )}{\partial {\sigma }^2}=0=>{\hat{\sigma }}^2=\frac{1}{n}{\sum }_{i=1}^n(x_i-\mu {)}^2$
  即：$\hat{\theta }=(\hat{\mu },{\hat{\sigma }}^2)$,$\hat{\theta }$：表示优化后的$\theta$值,读：hat。

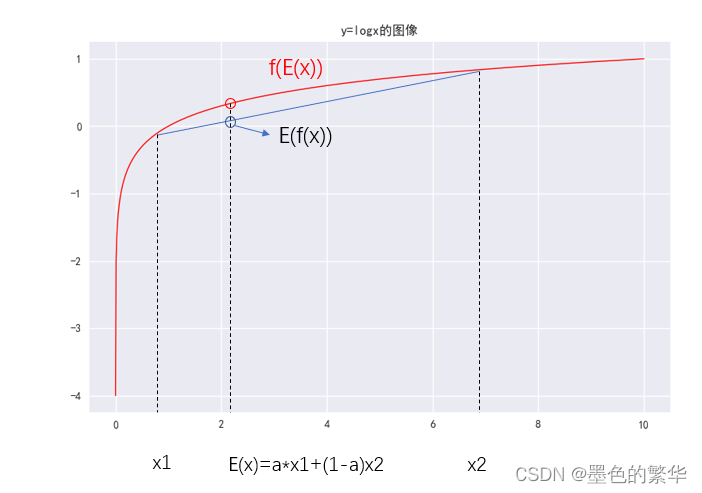
• Jensen不等式:
  对于f(x)的凹函数：瞪眼看，有$f(E(x))\geqq E(f(x))$
  即：x的期望的函数值 大于等于 函数值f(x)的期望
  仅当：$x_1=x_2$为同一点时，$f(E(x))=E(f(x))$
  凸函数相反。
  
  5）EM 算法之步骤
  举个例子，体验神奇：

1. 你看到29 个同学的身高数据如下图。（是男娃子，女娃子？不是你能知道的哟！（男：17 vs 女：12），我是从上帝视角给你参考的。）
   

2. 已知：男娃子身高高一些，男娃子，女娃子都符合各自的正态分布。

3. 求：男女娃子各个多少，他们的分布参数${\mu }_{男},{\sigma }_{男},{\mu }_{女},{\sigma }_{女}$。

4. 过程如图（请仔细看！至少读一遍, 会有代码的。）
   E: 期望步骤：求$p(z|x,\theta )，p(z|\theta )$
   M: 最大化步骤：利用对数极大似然求$\theta$
   

注意： 一个人是男是女的概率$$p(z_{男}|x,\theta )=p(z_{男}|\theta )\ast p(x|z_{男},\theta )/p(x|\theta )----i$$
$$p(z_{女}|x,\theta )=p(z_{女}|\theta )\ast p(x|z_{女},\theta )/p(x|\theta )----ii$$
有：$p(z_{男}|x,\theta )/p(z_{女}|x,\theta )=p(z_{男}|\theta )\ast p(x|z_{男},\theta )/p(z_{女}|\theta )\ast p(x|z_{女},\theta )，而p(z_{男}|\theta )通过迭代提供，而p(x|z_{男},\theta )={\mathrm{N}}_{男}({\mu }_{男},{\sigma }_{男})提供，女娃子相关类似$
而：$p(z_{男}|x,\theta )+p(z_{女}|x,\theta )=1$
可是算出：$p(z_{男}|x,\theta ),p(z_{女}|x,\theta )$

具体细节如excel:

EM 算法结果，人数：男，17.76 vs 17；女，11.24 vs 12 相差不足一个! 平均身高：男 1.73 vs1.75；女 1.64 vs1.62。

6）EM 算法之原理
对于出现的样本X:{$x_1,x_2,...,x_n$}，对数极大似然:
$$\theta =\underset{\theta }{\mathrm{argmax}}\sum _{i=1}^{n}ln(p(x_i|\theta ))$$
考虑到隐变量：z: {$z_1,z_2,...$}
$$\theta =\underset{\theta }{\mathrm{argmax}}\sum _{i=1}^{n}ln\sum _{z}p(x_i,z|\theta )$$

构造一个$Q(z)$，使得${\sum }_{z}Q(z)=1$，而有：
$$\theta =\underset{\theta }{\mathrm{argmax}}\sum _{i=1}^{n}ln\sum _{z}Q(z)\frac{p(x_i,z|\theta )}{Q(z)}$$

ln 为凹函数，利用Jensen不等式$f(E(x))\geqq E(f(x))$：
$$\theta =\underset{\theta }{\mathrm{argmax}}\sum _{i=1}^{n}ln\sum _{z}Q(z)\frac{p(x_i,z|\theta )}{Q(z)}\geqq \theta =\underset{\theta }{\mathrm{argmax}}\sum _{i=1}^n\sum _{z}Q(z)ln(\frac{p(x_i,z|\theta )}{Q(z)})$$
注意相等时：$\frac{p(x_i,z|\theta )}{Q(z)}=C$ ，C为常量。

$$\sum _{z}Q(z)=1推出\sum _{z}p(x_i,z|\theta )=C$$

$$Q(z_i)=\frac{p(x_i,z|\theta )}{C}=\frac{p(x_i,z|\theta )}{{\sum }_{z}p(x_i,z|\theta )}=\frac{p(x_i,z|\theta )}{p(xi|\theta )}$$

即：$$Q(z_i)=\frac{p(x_i,z|\theta )}{p(xi|\theta )}=p(z|x_i,\theta )$$
相当于算出男、女比例，根据这个参数。M 对数极大似然优化：$$\hat{\theta }=\underset{\theta }{\mathrm{argmax}}\sum _{i=1}^n\sum _{z}Q(z)ln(\frac{p(x_i,z|\theta )}{Q(z)})$$

例如对于$ln(l(\theta ))$其偏导，如果是高斯混合分布,k轮迭代有：
$${\gamma }_{i,z}=\frac{p(z|\theta )\ast p(x|z,\theta )}{{\sum }_{z}p(z|\theta )\ast p(x|z,\theta )}$$

${\mu }_z=\frac{\gamma x_i}{{\sum }_{i=1}^n\gamma }$ 注意:有多个类型分布，就有多个${\mu }_z$

${\sigma }_z=\frac{{\sum }_{i=1}^n\gamma (x_i-u_z{)}^2}{{\sum }_{i=1}^n\gamma }$

7）EM 算法之收敛

程序判定收敛，只证明单调递增。
在t+1 次计算，${\theta }^t$为常量，${\theta }^{(t+1)}$为对数极大似然优化量
所以有
$$ln(l({\theta }^{(t+1)}))\geqq \sum _{i=1}^n\sum _{z}Q(z)ln(\frac{p(x_i,z|{\theta }^{(t+1)})}{Q(z)})\geqq \sum _{i=1}^n\sum _{z}Q(z)ln(\frac{p(x_i,z|{\theta }^t)}{Q(z)})$$

又因为Q(z)，求的时候有：$\frac{p(x_i,z|\theta )}{Q(z)}=C$，Jensen不等式取等号：
所以有：
$$\sum _{i=1}^n\sum _{z}Q(z)ln(\frac{p(x_i,z|{\theta }^t)}{Q(z)})=ln(l({\theta }^t))$$

因此：
$$ln(l({\theta }^{(t+1)}))\geqq ln(l({\theta }^t))$$，为递增，得证。

8）EM 算法之python 代码

# coding=utf-8
import numpy as np
import math

# 作者dls

# 生成样本
height_M = np.random.normal(loc=1.75, scale=0.07, size=17)  # 正态分布，男生
height_F = np.random.normal(loc=1.62, scale=0.07, size=12)  # 正态分布，女生
dataset = arr4 = np.concatenate((height_F, height_M), axis=0)

# print(dataset)
# 初始化
gamma = [0.5, 0.5]  # 男女概率p(z|θ)
theta = [1.70, 0.01, 1.62, 0.01]  # 男女分布参数


# part_M = []  # 初始化每个人男的比例
# part_F = []  # 初始化每个人女的比例


# 密度分布函数
def normal_distribution(x, mean, sigma):
    return np.exp(-1 * ((x - mean) ** 2) / (2 * (sigma ** 2))) / (math.sqrt(2 * np.pi) * sigma)


# 更新男女分布
def update_Q(dataset, theta, gamma):
    part_M = []
    part_F = []
    for data in dataset:
        dis_M = normal_distribution(data, theta[0], theta[1])
        dis_F = normal_distribution(data, theta[2], theta[3])
        part_M_data = dis_M * gamma[0] / (dis_M * gamma[0] + dis_F * gamma[1])
        part_M.append(part_M_data)
        part_F.append(1 - part_M_data)
    gamma[0] = np.sum(part_M)
    gamma[1] = np.sum(part_F)
    return part_M, part_F, gamma


# 更新平均值
def update_mean(dataset, part):
    sum_total = 0
    sum_count = 0
    for i in range(len(part)):
        sum_total = sum_total + part[i] * dataset[i]
        sum_count = sum_count + part[i]
    return sum_total / sum_count


# 更新sigma
def update_sigma(dataset, part, u):
    sum_total = 0
    sum_count = 0
    for i in range(len(part)):
        sum_total = sum_total + part[i] * (dataset[i] - u) * (dataset[i] - u)
        sum_count = sum_count + part[i]
    return math.sqrt(sum_total / sum_count)


part_M, part_F, gamma = update_Q(dataset, theta, gamma)
# print("男的权重",part_M)

theta[0] = update_mean(dataset, part_M)
theta[1] = update_sigma(dataset, part_M, theta[0])
theta[2] = update_mean(dataset, part_F)
theta[3] = update_sigma(dataset, part_M, theta[2])

for i in range(20):
    # E 步骤
    part_M, part_F, gamma = update_Q(dataset, theta, gamma)
    # print("男的权重",part_M)

    # M 步骤
    theta[0] = update_mean(dataset, part_M)
    theta[1] = update_sigma(dataset, part_M, theta[0])
    theta[2] = update_mean(dataset, part_F)
    theta[3] = update_sigma(dataset, part_M, theta[2])
    print("开始次数", i + 1)
    print("男女概率", gamma)
    print("分布参数", theta)
    print("*" * 80)
    print()
# print(gamma)

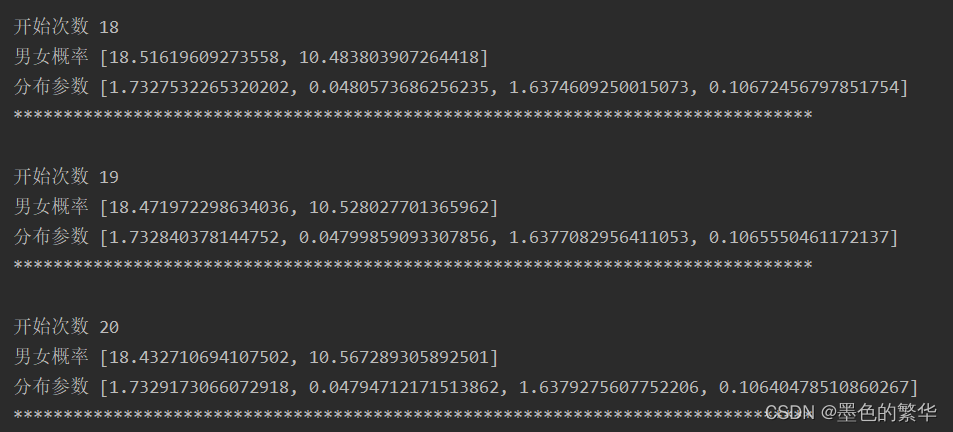
误差比较小。

9）EM 算法之感谢
简博士 大神 女神 的视频，收益匪浅！
https://www.bilibili.com/video/BV1No4y1o7ac/?spm_id_from=333.999.0.0