python多重继承的MRO算法选择: 经典方式、Python2.2 新式算法、Python2.3 新式算法(C3)。Python 3中只保留了最后一种,即C3算法
C3算法的解析:
1.多继承UML图:
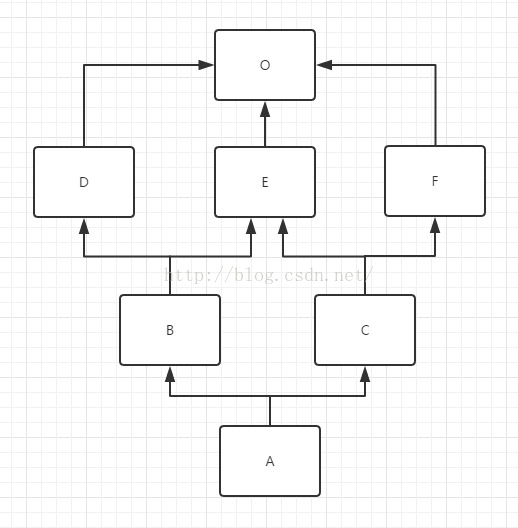
备注:O==object
2.python-C3算法解析:
#C3 定义引用开始
C3 算法:MRO是一个有序列表L,在类被创建时就计算出来。
L(Child(Base1,Base2)) = [ Child + merge( L(Base1) , L(Base2) , Base1Base2 )]
L(object) = [ object ]
L的性质:结果为列表,列表中至少有一个元素即类自己。
+ : 添加到列表的末尾,即 [ A + B ] = [ A,B ]
merge: ① 如果列表空则结束,非空 读merge中第一个列表的表头,
② 查看该表头是否在 merge中所有列表的表尾中。
②-->③ 不在,则 放入 最终的L中,并从merge中的所有列表中删除,然后 回到①中
②-->④ 在,查看 当前列表是否是merge中的最后一个列表
④-->⑤ 不是 ,跳过当前列表,读merge中下一个列表的表头,然后 回到 ②中
④-->⑥ 是,异常。类定义失败。
表头: 列表的第一个元素 (列表:ABC,那么表头就是A,B和C就是表尾)
表尾: 列表中表头以外的元素集合(可以为空)
merge 简单的说即寻找合法表头(也就是不在表尾中的表头),如果所有表中都未找到合法表头则异常。
#C3定义引用结束
例如:
L(D) = L(D(O))
= D + merge(L(O))
= D + O
= [D,O]
L(B) = L(B(D,E))
= B + merge(L(D) , L(E))
= B + merge(DO , EO) # 第一个列表DO的表头D,其他列表比如EO的表尾都不含有D,所以可以将D提出来,即D是合法表头
= B + D + merge(O , EO) #从第一个开始表头是O,但是后面的列表EO的表尾中含有O所以O是不合法的,所以跳到下一个列表EO
= B + D + E + merge(O , O)
= [B,D,E,O]
同理:
L(C) = [C,E,F,O]
L(A(B,C)) = A + merge(L(B),L(C),BC)
= A + merge(BDEO,CEFO,BC)#B是合法表头
= A + B + merge(DEO,CEFO,C)#D是合法表头
= A + B + D + merge(EO,CEFO,C)#E不是合法表头,跳到下一个列表CEFO,此时C是合法表头
= A + B + D + C + merge(EO,EFO)#由于第三个列表中的C被删除,为空,所以不存在第三个表,只剩下两个表;此时E是合法表头
= A + B + D + C + E + merge(O,FO)#O不是合法表头,跳到下一个列表FO,F是合法表头,
= A + B + D + C + E + F + merge(O,O)#O是合法表头
= A + B + D + C + E + F + O
= [A,B,D,C,E,F,O]
获取C3的数组列表,可以梳理清楚子类执行过程中向上执行的顺序
























 353
353

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








