题目链接
3757: 苹果树
Time Limit: 20 Sec Memory Limit: 256 MBSubmit: 1674 Solved: 550
[ Submit][ Status][ Discuss]
Description
神犇家门口种了一棵苹果树。苹果树作为一棵树,当然是呈树状结构,每根树枝连接两个苹果,每个苹果都可以沿着一条由树枝构成的路径连到树根,而且这样的路径只存在一条。由于这棵苹果树是神犇种的,所以苹果都发生了变异,变成了各种各样的颜色。我们用一个到n之间的正整数来表示一种颜色。树上一共有n个苹果。每个苹果都被编了号码,号码为一个1到n之间的正整数。我们用0代表树根。只会有一个苹果直接根。
有许许多多的人来神犇家里膜拜神犇。可神犇可不是随便就能膜拜的。前来膜拜神犇的人需要正确回答一个问题,才能进屋膜拜神犇。这个问题就是,从树上编号为u的苹果出发,由树枝走到编号为v的苹果,路径上经过的苹果一共有多少种不同的颜色(包括苹果u和苹果v的颜色)?不过神犇注意到,有些来膜拜的人患有色盲症。具体地说,一个人可能会认为颜色a就是颜色b,那么他们在数苹果的颜色时,如果既出现了颜色a的苹果,又出现了颜色b的苹果,这个人只会算入颜色b,而不会把颜色a算进来。
神犇是一个好人,他不会强人所难,也就会接受由于色盲症导致的答案错误(当然答案在色盲环境下也必须是正确的)。不过这样神犇也就要更改他原先数颜色的程序了。虽然这对于神犇来说是小菜一碟,但是他想考验一下你。你能替神犇完成这项任务吗?
Input
Output
输出一共m行,每行仅包含一个整数,代表这个人应该数出的颜色种数。
Sample Input
1 1 3 3 2
0 1
1 2
1 3
2 4
3 5
1 4 0 0
1 4 1 3
1 4 1 2
Sample Output
1
2
HINT
这一题似乎已经不能提交了,不过通过看这题的博客我基本懂了树上莫队,看了这篇博客。
下面做一些补充:
序列上的莫队是把询问按照左端点分块了……可是树上没有左端点,怎么办呢?我们把树分块。
按照DFS时间戳顺序,将树分成O(sqrt(n))个大小为O(sqrt(n))的块,那么树上的莫队询问排序的第一关键字就是第一个节点所在的块了!
这样分块以后,任意两个块之间的距离也是O(sqrt(n))级别的,所以时间复杂度是有保证的。
第二个关键字自然就是节点的DFS时间戳了!
但是,还有一个问题。树上的区间要怎么转移呢?要怎么从一个区间变到另一个区间呢?
这就有些难了,因为树上有LCA,貌似不好处理。
Orz了wyfcyx后,找到了vfk的博客看了一下。
用S(v, u)代表 v到u的路径上的结点的集合。
用root来代表根结点,用lca(v, u)来代表v、u的最近公共祖先。
那么
S(v, u) = S(root, v) xor S(root, u) xor lca(v, u)
其中xor是集合的对称差。
简单来说就是节点出现两次消掉。
lca很讨厌,于是再定义
T(v, u) = S(root, v) xor S(root, u)
观察将curV移动到targetV前后T(curV, curU)变化:
T(curV, curU) = S(root, curV) xor S(root, curU)
T(targetV, curU) = S(root, targetV) xor S(root, curU)
取对称差:
T(curV, curU) xor T(targetV, curU)= (S(root, curV) xor S(root, curU)) xor (S(root, targetV) xor S(root, curU))
由于对称差的交换律、结合律:
T(curV, curU) xor T(targetV, curU)= S(root, curV) xorS(root, targetV)
两边同时xor T(curV, curU):
T(targetV, curU)= T(curV, curU) xor S(root, curV) xor S(root, targetV)
发现最后两项很爽……哇哈哈
T(targetV, curU)= T(curV, curU) xor T(curV, targetV)
(有公式恐惧症的不要走啊 T_T)
也就是说,更新的时候,xor T(curV, targetV)就行了。
即,对curV到targetV路径(除开lca(curV, targetV))上的结点,将它们的存在性取反即可。
”
——vfk博客
这样就很好处理了,只要把LCA扔出去,考虑剩下的部分,转移一下就可以了。查答案的时候再把LCA那个点反过来,就能统计出答案了。
这样,类比序列上的莫队,我们对树上的询问也可以分块了,时间复杂度同样是O(nsqrt(n))。
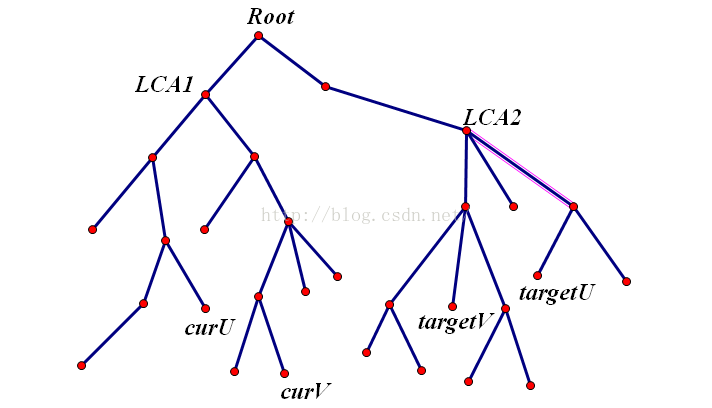
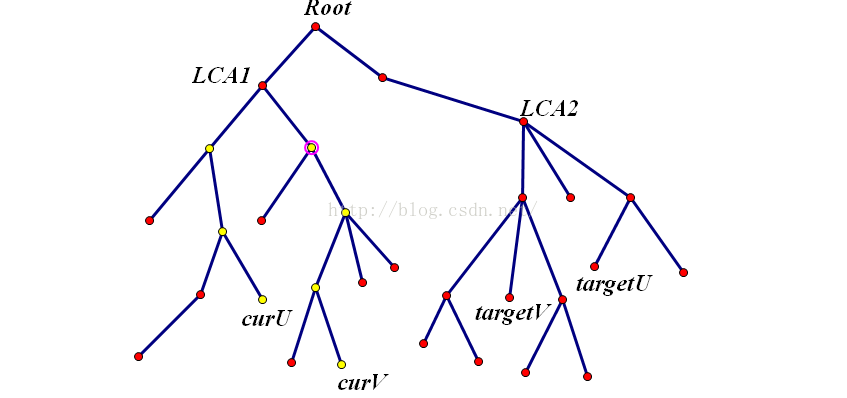
关于将lca放出去的原因,可以看下面的图文加深理解
假设有这样的一棵树和两组询问
现在的答案是黄点的答案
而我们要求的是这些蓝点的答案
考虑怎么从黄点变成蓝点?
就是XOR上S(curV,root) xor S(curV,targetV),也就是对curV到targetV的路径上的点(除了lca)的存在性取反。
这样我们就可以先把LCA扔出去,算剩下部分的答案,再加上lca的贡献,然后就ok了
给这一题博客上的代码加了注释,看看代码就懂如何操作了
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
inline int getint()
{
char c=getchar();
int con=0;
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9') con=con*10+c-'0',c=getchar();
return con;
}
const int MAXN=100010;
int n,m,K,lca,u,v,c[MAXN],dfn[MAXN],belongn[MAXN];
int tot,root,dfs_clock,remain;
int head[MAXN],to[MAXN],next[MAXN],cnt;
int anc[MAXN][21],dep[MAXN],Log[MAXN];
int Stack[MAXN],top;
int p[MAXN],ans,con[MAXN];
bool used[MAXN];
struct Query
{
int u,v,a,b,sub;
friend bool operator<(const Query &i,const Query &j)
{
if(belongn[i.u]==belongn[j.u]) return dfn[i.v]<dfn[j.v];
else return belongn[i.u]<belongn[j.u];
}
}Q[MAXN];
inline void adde(int f,int t)
{
cnt++,to[cnt]=t,next[cnt]=head[f],head[f]=cnt;
cnt++,to[cnt]=f,next[cnt]=head[t],head[t]=cnt;
}
int DFS(int x)
{
int size=0;
dfn[x]=++dfs_clock;
for(int i=head[x];i;i=next[i])
if(to[i]!=anc[x][0])
{
dep[to[i]]=dep[x]+1,anc[to[i]][0]=x;
size+=DFS(to[i]);
if(size>=K) //为分块子结点数大于等于K时进行分块
{
tot++;
for(int i=1;i<=size;i++)
belongn[Stack[top--]]=tot;//Stack是一个栈,存储还未分块的结点编号
size=0;
}
}
Stack[++top]=x;
return size+1; //返回子节点中未分块数目加上自己本身
}
int LCA(int p,int q)
{
if(dep[p]<dep[q]) swap(p,q);
int d=dep[p]-dep[q];
for(int i=Log[d];i>=0;i--)
if(d&(1<<i)) p=anc[p][i];
for(int i=Log[n];i>=0;i--)
if(anc[p][i]!=anc[q][i]) p=anc[p][i],q=anc[q][i];
if(p!=q) return anc[p][0];
else return p;
}
void work(int u,int v,int lca)
{
while(u!=lca)
{
if(!used[u]) {p[c[u]]++,used[u]=true;if(p[c[u]]==1) ans++;}//used存储是否在当前路径上
else {p[c[u]]--,used[u]=false;if(p[c[u]]==0) ans--;}
u=anc[u][0];
}
while(v!=lca)
{
if(!used[v]) {p[c[v]]++,used[v]=true;if(p[c[v]]==1) ans++;}
else {p[c[v]]--,used[v]=false;if(p[c[v]]==0) ans--;}
v=anc[v][0];
}
}
int main()
{
n=getint(),m=getint();
K=(int)sqrt(n);
for(int i=1;i<=n;i++) c[i]=getint();
for(int i=1;i<=n;i++)
{
u=getint(),v=getint();
if(u==0) root=v;
else if(v==0) root=u;
else adde(u,v);
}
for(int i=1;i<=m;i++)
{
Q[i].u=getint(),Q[i].v=getint();
Q[i].a=getint(),Q[i].b=getint();
Q[i].sub=i;
}
remain=DFS(root); //求还未分块的结点数目
for(int i=1;i<=remain;i++) belongn[Stack[top--]]=tot; //进行分块
sort(Q+1,Q+m+1); //排序
Log[0]=-1;
for(int i=1;i<=n;i++) Log[i]=Log[i>>1]+1; //lca部分
for(int i=1;i<=Log[n];i++)
for(int j=1;j<=n;j++)
anc[j][i]=anc[anc[j][i-1]][i-1];
work(Q[1].u,Q[1].v,lca=LCA(Q[1].u,Q[1].v));
if(!used[lca]) {p[c[lca]]++,used[lca]=true;if(p[c[lca]]==1) ans++;}//lca特殊处理
else {p[c[lca]]--,used[lca]=false;if(p[c[lca]]==0) ans--;}
con[Q[1].sub]=ans;
if(p[Q[1].a]!=0&&p[Q[1].b]!=0) con[Q[1].sub]--; //对于色盲颜色a,b进行判断,似乎条件还需要判断a,b是否相等?
if(!used[lca]) {p[c[lca]]++,used[lca]=true;if(p[c[lca]]==1) ans++;}//lca取反
else {p[c[lca]]--,used[lca]=false;if(p[c[lca]]==0) ans--;}
for(int i=2;i<=m;i++)
{ //后面的类似,不过注意work函数中参数是上一次结点和此次结点
work(Q[i-1].u,Q[i].u,LCA(Q[i-1].u,Q[i].u));
work(Q[i-1].v,Q[i].v,LCA(Q[i-1].v,Q[i].v));
lca=LCA(Q[i].u,Q[i].v);
if(!used[lca]) {p[c[lca]]++,used[lca]=true;if(p[c[lca]]==1) ans++;}
else {p[c[lca]]--,used[lca]=false;if(p[c[lca]]==0) ans--;}
con[Q[i].sub]=ans;
if(p[Q[i].a]!=0&&p[Q[i].b]!=0&&Q[i].a!=Q[i].b) con[Q[i].sub]--;
if(!used[lca]) {p[c[lca]]++,used[lca]=true;if(p[c[lca]]==1) ans++;}
else {p[c[lca]]--,used[lca]=false;if(p[c[lca]]==0) ans--;}
}
for(int i=1;i<=m;i++) printf("%d\n",con[i]);
return 0;
}
























 696
696

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








