ACM MM 24 | DRMF: Degradation-Robust Multi-Modal Image Fusion via Composable Diffusion Prior

ACM MM 24 | DRMF: 基于可组合扩散先验的鲁棒多模态图像融合

DRMF: Degradation-Robust Multi-Modal Image Fusion via Composable Diffusion Prior [论文下载] [Code]

引用格式

@inproceedings{Tang2024DRMF,
title={DRMF: Degradation-Robust Multi-Modal Image Fusion via Composable Diffusion Prior},
author={Tang, Linfeng and Deng, Yuxin and Yi, Xunpeng and Yan, Qinglong and Yuan, Yixuan and Ma, Jiayi},
booktitle=Proceedings of the ACM International Conference on Multimedia,
pages={8546–8555},
year={2024}
}

摘要

现有的多模态图像融合算法通常是为高质量图像设计的，无法处理降质（例如，低光、低分辨率和噪声），这限制了图像融合在实践中发挥其潜力。在这项工作中，我们提出了一种鲁棒多模态图像融合（DRMF）方法，利用扩散模型强大的生成特性来对抗图像融合过程中的各种降质。我们的关键洞见在于，由不同模态和降质驱动的生成式扩散模型在去噪过程中是内在互补的。具体来说，我们为不同模态预训练了多个鲁棒的条件扩散模型来处理降质。随后，我们设计了扩散先验组合模块，以整合来自预训练的单模态模型的生成先验，从而实现有效的多模态图像融合。大量实验表明，DRMF在红外-可见光和医学图像融合方面表现出色，即使在复杂的降质条件下也是如此。我们的代码已在 https://github.com/Linfeng-Tang/DRMF 上开源。

关键词：多模态图像融合；图像增强；扩散模型

图 1：在 MMIF 任务的复杂场景中的融合示意图。DDFM [66] 和 DIVFusion [40] 分别是基于扩散和光照鲁棒的图像融合方法。DiffLL [12] 和 CAT [2] 是最先进的图像修复方法。

1 引言

多模态图像融合（MMIF）是一种关键的图像增强技术，它聚合来自不同传感器或模态的重要信息，以获得全面的场景表示。红外-可见光图像融合（IVIF）和医学图像融合（MIF）是MMIF最具代表性的任务。IVIF旨在融合红外（IR）图像中的基本热辐射信息和可见光（VI）图像中的丰富纹理。融合结果可以克服红外图像受噪声和低分辨率影响的局限性，以及可见光图像受光照和伪装影响的局限性。MIF则致力于将功能图像中的功能和代谢信息与结构图像中的结构和解剖信息整合到单张图像中，以辅助后续的疾病诊断和治疗。凭借充分的信息聚合和令人愉悦的视觉效果，MMIF被广泛应用于各种领域，如智能医疗服务、夜间辅助驾驶、以及场景理解。

近年来，基于自编码器（AE）、卷积神经网络（CNN）、生成对抗网络（GAN）和Transformer的框架主导了MMIF领域。此外，具有强大分布建模和生成能力的扩散模型在MMIF中显示出巨大潜力。DDFM利用分数匹配技术将预训练的自然图像扩散模型的生成先验迁移到MMIF中。然而，分数匹配的实现涉及繁琐的设计，并且需要为每个特定场景重新优化目标函数，这非常耗时。此外，自然图像与多模态图像之间的分布差异限制了预训练扩散模型在MMIF中的性能。

此外，大多数融合方法都是为正常场景量身定制的。如图1（I）所示，现实夜景中的可见光图像经历了严重的光照退化，即使是先进的基于扩散模型的方法（如DDFM）也难以有效表示场景信息。一些工作试图在挑战性场景中同时增强和聚合互补信息。DIVFusion首先利用Retinex理论提取与反射率和光照相关的特征。然后，它仅在后续融合中整合与反射率相关的特征，以减轻光照退化的负面影响。然而，由于光照分量被完全丢弃，DIVFusion的融合结果（如图1（I d）所示）显得不自然，并存在明显的颜色失真。

值得注意的是，挑战性场景中的源图像可能受到多种退化的影响，包括噪声、低对比度、低分辨率、低光等。如图1（II）所示，现有的融合方法难以有效处理复合退化，导致融合结果出现噪声和模糊，这极大地限制了MMIF的实际应用。尽管可以使用一些预处理技术（例如用于低光图像增强的DiffLL和用于去噪及超分辨率的CAT）来预增强源图像，但多个级联任务之间的耦合性差导致误差放大，从而合成了不理想的融合结果，如图1（I-c）和（II-c）所示。

为了应对这些挑战，我们提出了一种基于可组合扩散先验的鲁棒融合方法，称为DRMF，这是一种用于MMIF的新型基于扩散的范式。DRMF充分利用了由不同模态和退化驱动的扩散模型的内在互补潜力。我们首先预训练多个以退化源图像为条件的鲁棒条件扩散模型，以估计相应高质量图像的分布。由于生成式扩散先验由高斯噪声表征，各种先验可以在噪声空间中组合。具体来说，给定t步的融合样本$x_t^f$，由第i个模态驱动的扩散模型${ϵ}_{\theta }^i$估计噪声（即生成先验）$n_t^i$，以逼近第i个模态的高质量修正版本。然后，扩散先验组合模块估计不同模态驱动的先验$n_t^i$的权重，并生成下一个样本$x_{t-1}^f$。逐渐地，DRMF在以退化输入为条件下，生成高质量的融合图像。如图1所示，DRMF有效处理复杂退化，生成令人印象深刻的融合结果，既突出了重要目标，又生动地描绘了场景细节。

我们的主要贡献有两方面：

• 我们提出了一种新颖的基于扩散模型的MMIF框架，它利用扩散模型强大的生成特性来减轻源图像中的各种复杂退化。
• 我们开发了一个扩散先验组合模块来聚合来自不同模态的生成式扩散先验，有效利用了由各种模态和退化驱动的扩散模型的互补性。

2 相关工作

多模态图像融合

深度学习的蓬勃发展为MMIF领域注入了活力。AE、CNN、GAN和Transformer是基于深度学习的MMIF方法中使用的主要网络架构。为响应后续高级视觉任务的实际需求，图像融合界提出了许多语义驱动的方法，这些方法约束融合网络保留更丰富的语义线索。此外，RFNet、UMF-CMGR、SuperFusion和MURF联合建模图像配准和融合任务，校正实际拍摄中的视差和像差。此外，一些通用方法统一地完成各种图像融合任务。具体来说，认识到源图像通常会受到退化的影响，Tang等人和Wang等人设计了光照鲁棒的融合方法，这些方法考虑了低光图像增强和信息融合。然而，这些方法专门为光照退化设计，无法解决其他常见退化，如噪声和低分辨率。

扩散模型

最近，扩散模型在计算机视觉领域获得了广泛关注，它从估计的目标分布中采样高质量图像。得益于其强大的生成能力，扩散模型已被应用于各种低级视觉任务，如文本到图像生成、图像操纵、超分辨率、去雨、去模糊和低光图像增强，并持续取得显著成果。然而，可组合扩散模型的提出是为了利用多模态条件来更准确地控制生成过程。扩散模型也被引入到MMIF领域。Dif-Fusion首次将扩散模型的去噪网络用作强大的特征提取器，而整个图像融合过程与扩散模型分离。DDFM结合了分数匹配和预训练的无条件扩散模型，将从自然图像中学到的生成先验转移到多模态图像以进行图像融合。值得注意的是，现有的基于扩散模型的方法并非专门为MMIF中的挑战而设计，扩散模型的卓越生成能力尚未被释放。

3 方法论

给定互补的退化源图像 { x c i } \{x_c^i\} {xci​}，其中 i ∈ { i r , v i , c t , m r i } i \in \{ir, vi, ct, mri\} i∈{ir,vi,ct,mri}，我们的方法从随机高斯噪声$x_T$开始，通过以 { x c i } \{x_c^i\} {xci​}为条件的逐步去噪生成高质量的融合图像$x^f$。我们设计了一个扩散先验组合模块，以组合来自多个扩散模型 { ϵ θ i } \{\epsilon_\theta^i\} {ϵθi​}的噪声 { n t i } \{n_t^i\} {nti​}，并在去噪过程中推断下一个融合样本。特别地，估计的噪声表征了由不同模态和退化驱动的鲁棒扩散先验，从而我们可以实现多模态信息聚合。我们的采样过程遵循标准的条件扩散模型。因此，下面我们依次介绍典型的扩散模型、鲁棒条件扩散模型和扩散先验组合模块。

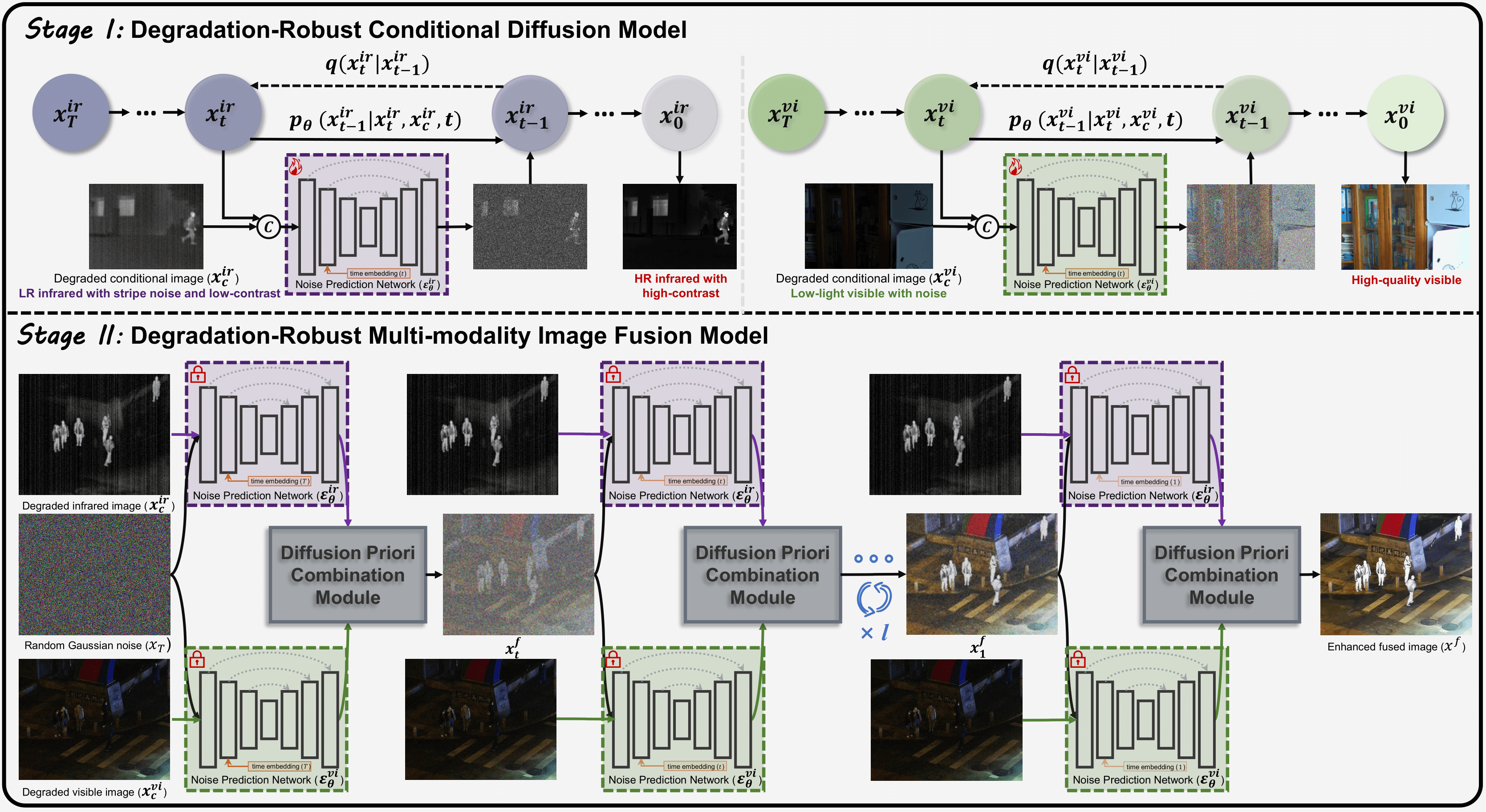
图2. 所提出的 DRMF 框架（以红外-可见光融合为例）。阶段 I 展示了 DRCDMs 的处理流程；阶段 II 表示利用预训练的退化鲁棒扩散先验直接生成融合结果的过程。

3.1 扩散模型基础

去噪扩散概率模型是一种经典的生成模型，它使用马尔可夫链将复杂的数据分布转换为简单的正态分布。然后通过迭代去噪从噪声分布中恢复所需的数据分布。在前向过程中，数据分布$x_0\sim p(x_0)$通过预定义的马尔可夫链引入高斯噪声而逐渐被破坏，该过程满足以下分布：
$$q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{{\alpha }_t}{x}_{t-1},{\beta }_{t}I)(1)$$
其中${\beta }_t$控制在第t步添加的噪声方差，${\alpha }_t=1-{\beta }_t$。因此，边际分布可以导出为：
$$q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{{\bar{\alpha }}_t}{x}_0,{\bar{\beta }}_{t}I)(2)$$
其中${\bar{\alpha }}_t={\Pi }_{i=1}^t{\alpha }_i$且${\bar{\beta }}_t=1-{\bar{\alpha }}_t$。当t趋近于一个大值T时，${\bar{\alpha }}_T$趋于0，且$q(x_T|x_0)$近似于正态分布$\mathcal{N}(0,I)$，前向过程结束。

反向过程从一个高斯噪声$x_T$开始，通过马尔可夫链迭代地对其进行去噪以生成清晰的图像：
$$p_{\theta }(x_{t-1}|x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\sigma }_t^{2}I)(3)$$
如[8]中所述，均值${\mu }_{\theta }(x_t,t)$是基于噪声估计网络${ϵ}_{\theta }$（参数为$\theta$）的估计结果计算的，而方差${\sigma }_t^2$是一个与时间相关的常数。具体地，上述过程公式化为：
$$\begin{array}{rl}{\mu }_{\theta }(x_t,t)& =\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }(x_t,t))\\ {\sigma }_t^2& =\frac{(1-{\bar{\alpha }}_{t-1})}{(1-{\bar{\alpha }}_t)}{\beta }_t(4)\end{array}$$
最终，优化目标定义为：
$${\mathbb{E}}_{x_0,n_t,t}\left[\Vert n_t-{ϵ}_{\theta }(\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}{n}_t,t){\Vert }^2\right](5)$$
其中$n_t$是从标准高斯噪声中采样的。

去噪扩散隐式模型为预训练的扩散模型提供了一种加速的确定性采样方式，其中前向过程遵循非马尔可夫过程。边际分布$q(x_t|x_0)$仍然服从公式(2)，而公式(4)中的均值被重新表述为：
$${\mu }_{\theta }(x_t,t)=\sqrt{{\bar{\alpha }}_{t-1}}{\hat{x}}_0+\sqrt{1-{\bar{\alpha }}_{t-1}-{\lambda }_t^2}{ϵ}_{\theta }(x_t,t)(6)$$
其中${\hat{x}}_0=\frac{x_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_{\theta }(x_t,t)}{\sqrt{{\bar{\alpha }}_t}}$表示当前步骤估计的$x_0$，${\lambda }_t$是控制边际分布方差的可调超参数。因此，公式(4)中的${\sigma }_t^2$被设置为${\lambda }_t^2$。

3.2 鲁棒条件扩散

条件扩散模型在图像生成、增强和退化图像恢复领域大放异彩。然而，MMIF中的扩散模型主要用于提取特征和提供自然图像的常规生成先验，而没有解决退化问题。在这项工作中，我们首先提出了鲁棒条件扩散模型（DRCDMs）来恢复退化的源图像。如图2所示，给定退化图像$x_c^i$和高质量版本$x_0^i$，训练阶段的前向过程遵循公式(1)，即$q(x_t^i|x_{t-1}^i)=\mathcal{N}(x_t^i;\sqrt{{\alpha }_t}{x}_{t-1}^i,{\beta }_{t}I)$。反向过程定义为$p_{\theta }(x_{t-1}^i|x_t^i,x_c^i)=\mathcal{N}(x_{t-1}^i;{\mu }_{\theta }(x_t^i,x_c^i,t),{\sigma }_t^{2}I)$，其中后验进一步以退化图像$x_c^i$为条件：
$${\mu }_{\theta }(x_t^i,x_c^i,t)=\frac{1}{\sqrt{{\alpha }_t}}(x_t^i-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }^i(x_t^i,x_c^i,t))(7)$$
具体来说，中间样本$x_t^i$与退化图像$x_c^i$拼接后输入噪声估计网络${ϵ}_{\theta }^i$，其中退化图像在提供有价值的语义和结构信息方面起着至关重要的作用。此外，优化目标被修改为：
$${\mathbb{E}}_{x_0^i,x_c^i,n_t,t}\left[\Vert n_t-{ϵ}_{\theta }^i(\sqrt{{\bar{\alpha }}_t}{x}_0^i+\sqrt{1-{\bar{\alpha }}_t}{n}_t,x_c^i,t){\Vert }^2\right](8)$$
在推理阶段，高质量的源图像通过迭代去噪生成，从标准高斯噪声开始，并由退化的条件图像引导。需要注意的是，在我们的解决方案中，DRCDMs不仅从退化图像中恢复高质量图像，还提供了鲁棒的生成式扩散先验，这些先验被用来直接生成高质量的融合图像。

3.3 扩散先验组合

经过预训练后，DRCDMs已经学习了高质量单模态图像的先验分布。这些先验由每个采样步骤预测的噪声决定。相关工作证实，组合来自多个扩散模型的噪声可以生成一个包含相应先验分布的结果。因此，为了直接生成一个携带高质量单模态先验特征的融合图像，我们设计了一个扩散先验组合模块（DPCM）来灵活地合并互补的噪声。

具体而言，如图2所示，我们使用预训练的DRCDMs从随机高斯噪声中反演图像，并根据以下规则在DDIM采样过程中更新均值：
$$\mu (x_t^f,x_c,t)=\sqrt{{\bar{\alpha }}_{t-1}}{\Sigma }_i{\gamma }_t^i{\hat{x}}_{0_t}^i+\sqrt{1-{\bar{\alpha }}_{t-1}-{\lambda }_t^2}\sum _i{\gamma }_t^i{ϵ}_{\theta }^i(x_t^f,x_C^i,t)(9)$$
其中${\hat{x}}_{0_t}^i=\frac{x_t^f-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_{\theta }^i(x_t^f,x_c^i,t)}{\sqrt{{\bar{\alpha }}_t}}$表示在t步从融合样本中，以$x_c^i$为条件的与第i个模态相关的估计样本。 { γ t i } t = 1 T \{\gamma_t^i\}_{t=1}^T {γti​}t=1T​是每个生成式扩散先验的序列权重，满足${\sum }_i{\gamma }_t^i=1$。

这样，DPCM的目标就是为每个模态估计序列权重。可学习的权重需要考虑几个因素。它们 1) 应该衡量不同模态的互补特性，2) 期望从高质量图像中学习，3) 受时间步长t的调制，以及 4) 受上一步权重的引导。因此，使用U-Net $\phi$生成权重的过程定义为：
$${\hat{\gamma }}_t^i=\phi (x_t^f,{\hat{x}}_{0_t}^i,{\gamma }_{t+1}^i,t)(10)$$
当前的融合样本$x_t^f$，预测的第i模态高质量样本${\hat{x}}_{0_t}^i$，以及来自上一步的权重${\gamma }_{t+1}^i$被连接并输入U-Net。为了归一化不同模态的权重，我们对所有权重 { γ ^ t i } \{\hat{\gamma}_t^i\} {γ^​ti​}执行softmax以获得最终的组合权重 { γ t i } \{\gamma_t^i\} {γti​}，即${\gamma }_t^i=\frac{\exp ({\hat{\gamma }}_t^i)}{{\sum }_j\exp ({\hat{\gamma }}_t^j)}$。具体来说，在涉及两个互补模态的融合任务中，估计一个权重${\gamma }_t^i$，另一个模态的权重可以直接导出为$1-{\gamma }_t^i$。

算法1. DPCM的训练流程。

我们还设计了相应的损失函数来优化权重预测网络$\phi$。融合损失定义为：
L f  ⁣ =  ⁣ ∑ i , t  ⁣ ( α t ∥ x ^ 0 t f − max ⁡ i ( { x ^ 0 i } ) ∥ 1 + α t ∥ ∇ x ^ 0 t f − max ⁡ i ( { ∇ x ^ 0 i } ) ∥ 1 ) ( 11 ) \mathcal{L}_f\!=\!\sum_{i,t}\!\left( \sqrt{\alpha_t} \| \hat{x}_{0_t}^f - \max_i(\{ \hat{x}_0^i\}) \|_1 + \sqrt{\alpha_t} \| \nabla \hat{x}_{0_t}^f - \max_i(\{ \nabla \hat{x}_0^i\})\|_1 \right) \quad (11) Lf​=i,t∑​(αt​ ​∥x^0t​f​−imax​({x^0i​})∥1​+αt​ ​∥∇x^0t​f​−imax​({∇x^0i​})∥1​)(11)
其中${\hat{x}}_{0_t}^f$表示在t步预测的清晰融合图像，${\hat{x}}_0^i$是由预训练的DRCDM恢复的高质量源图像。$\max (\cdot )$表示最大值聚合策略，$\nabla$表示梯度算子。随着去噪的进行（即t减小），估计的融合结果越来越接近期望的结果，因此我们用与时间相关的系数$\sqrt{{\alpha }_t}$来加权融合损失。此外，我们引入一个正则化项来约束组合权重${\gamma }_t^i$的平滑性，定义为：
$${\mathcal{L}}_{re}={\sum }_{i,t}\Vert \nabla {\gamma }_t^i{\Vert }_1(12)$$
$\phi$的完整目标函数是${\mathcal{L}}_f$和${\mathcal{L}}_{re}$的加权和：
$$\mathcal{L}={\mathcal{L}}_f+{\lambda }_{re}\cdot {\mathcal{L}}_{re}(13)$$
特别地，IVIF任务期望保留红外图像中的显著目标。为了实现这一点，我们设计了一个额外的掩码引导损失，利用显著目标掩码$m$来指导${\gamma }_t^{ir}$的学习，定义为：
$${\mathcal{L}}_m={\sum }_t-(m\log ({\gamma }_t^{ir})+(1-m)\log (1-{\gamma }_t^{ir}))(14)$$
DPCM 的训练过程如算法 1 所示（以红外-可见光融合，IVIF，为例）。该过程仅包含融合损失与正则化损失，以保证方法的通用性。在推理阶段，我们采用 DDIM 的快速采样策略，并根据式（10）在每一步更新 (x_f)，从而迭代生成高质量的融合图像。

4 实验

4.1 实现细节

我们分别训练多个DRCDMs。对于IVIF，我们最初在LOL和MSRS数据集上分别为VI和IR图像训练DRCDMs。LOL包含成对的低光和正常光图像。我们以降采样因子1/4对低对比度的IR图像进行下采样，并添加${\sigma }^2=15$的条纹噪声来模拟退化图像。高质量版本由MSRS提供。随后，在LOL上预训练的光照鲁棒CDM被用来增强MSRS中的VI图像。最后，我们使用来自MSRS的增强VI和高质量IR图像来训练DPCM，公式(15)中的显著目标掩码$m$由MSRS中的分割标签转换而来。

对于MIF，我们以高斯噪声（${\sigma }^2=25$）的形式为MRI图像引入退化，并使用1/4的下采样因子对CT图像进行下采样。在DRCDM训练期间，批量大小设置为64，学习率设置为$2\times 10^{-5}$，训练迭代次数为$2\times 10^6$，所有图像被随机裁剪为$64\times 64$。我们在1/4分辨率引入注意力机制以提高计算效率，其他设置遵循扩散模型的默认设置。

在训练DPCM时，我们采用DDIM确定性采样，${\lambda }_t=0$来生成融合图像，并将采样步数设置为5。批量大小和训练迭代次数调整为1和$1\times 10^5$，源图像被随机裁剪为$128\times 128$。

我们首先在LLVIP、MSRS和Harvard数据集的实际场景中评估所提方案的融合性能，这些数据集分别包含216、361和20个测试图像。然后，我们利用这些数据集中的退化图像来展示DRMF在解决MMIF复合退化问题上的优越性。此外，使用包含15张图像的LOL测试集来验证DRCDMs在处理退化方面的强大性能。

4.2 实际场景中的图像融合

我们首先考虑实际场景，其中所有源图像都直接由传感器捕获。DRMF与8种最先进（SOTA）的方法进行了比较，即DeFusion、TarDAL、U2Fusion、DIVFusion、LRRNet、MURF、PAIF和DDFM。IVIF和MIF任务的视觉比较如图3所示。在夜间IVIF场景中，DRMF有效地照亮了黑暗中的信息并增强了红外图像的对比度。我们的结果因此提供了明亮的背景和显著的目标。DIVFusion也能照亮可见光图像，但它存在过曝和颜色饱和度降低的问题。其他方法难以在黑暗中挖掘有价值的信息，甚至会减弱显著目标。如图3（a）所示，只有DRMF能够完全整合CT和MRI图像中的功能和结构信息，这得益于DPCM的自适应聚合能力。

使用MI、SF、SD和VIF的定量结果显示在表1中。一种SOTA低光增强（LLIE）方法（即DiffLL）被用来增强低光VI图像，以便公平地比较融合性能。Orig.表示实际的融合结果，而En.表示对VI图像进行LLIE后的融合结果。达到最佳的SD和VIF意味着我们的方法具有最佳的对比度和视觉效果。优越的MI表明DRMF有效地将有价值的信息从源图像传递到融合结果。可比较的SF表明我们的融合结果整合了丰富的纹理。

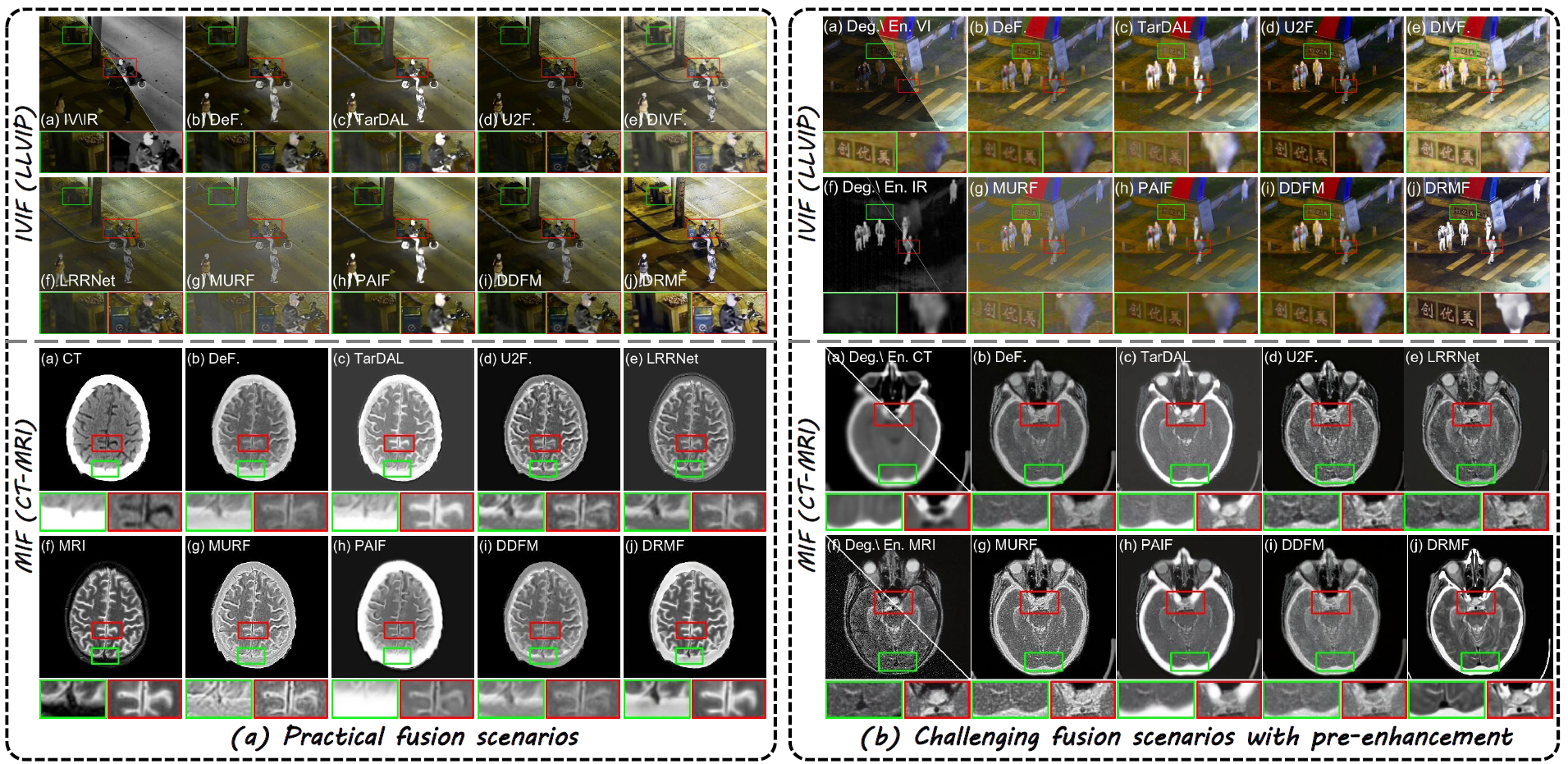
图3. IVIF和MIF在实际和挑战性融合场景中的可视化比较结果。

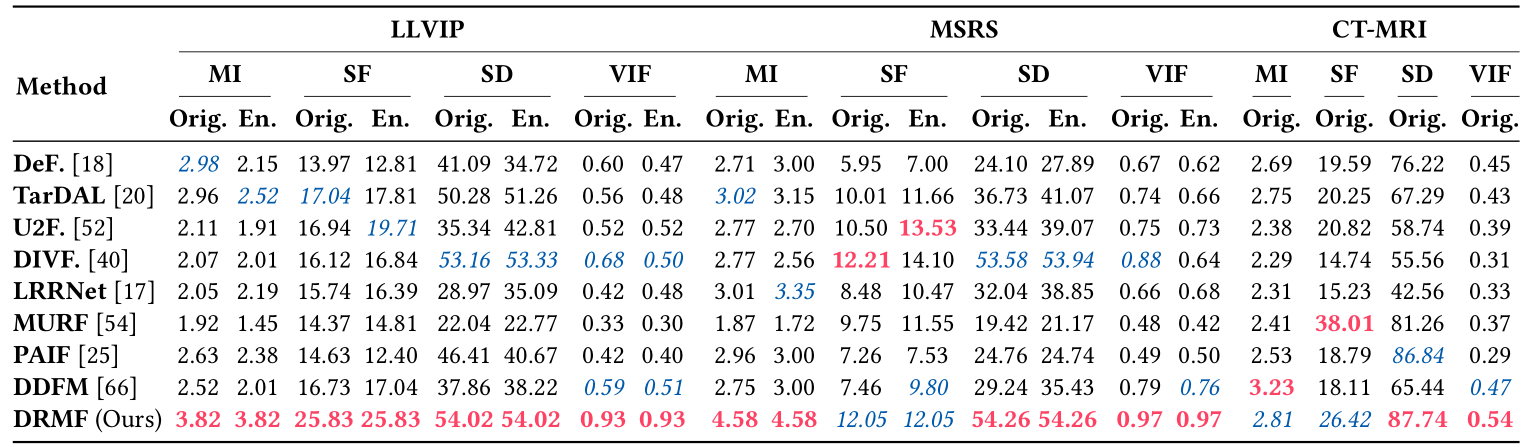
表1. 在实际融合场景中，DRMF与SOTA方法在IVIF和MIF任务上的定量比较结果。

4.3 挑战性场景中的图像融合

图3还展示了各种融合方法在挑战性场景下的视觉比较。具体来说，VI图像面临噪声和低光，而IR图像则存在低对比度、低分辨率和条纹噪声。CT和MRI图像则受到低分辨率和噪声的影响。这些退化是现实拍摄中典型的挑战。为了公平比较，我们使用DiffLL预增强VI图像，并微调CAT来对VI、IR和MRI图像进行去噪。CAT也经过微调以对IR和CT图像进行超分辨率处理。

如图3所示，即使在复杂的退化中，我们的融合结果也能清晰地呈现场景信息（例如，IVIF中丰富的纹理和突出的物体）。此外，只有DRMF能在MIF中生成最清晰、最锐利的融合图像，这归功于DRCDM卓越的退化消除能力。相比之下，其他替代方法受到复合退化的严重影响，降低了融合性能。级联的预增强方法减轻了一些影响，但放大了缺陷，导致性能不尽人意。表2进一步证实了DRMF在退化融合场景中的卓越性能。特别地，DRMF利用扩散模型的可组合特性，将增强有机地整合到融合任务中，避免了不同任务之间的不兼容性，并实现了令人印象深刻的性能。总之，IVIF和MIF上的定性和定量实验都证明了DRMF在抑制退化和聚合互补信息方面的优越性。

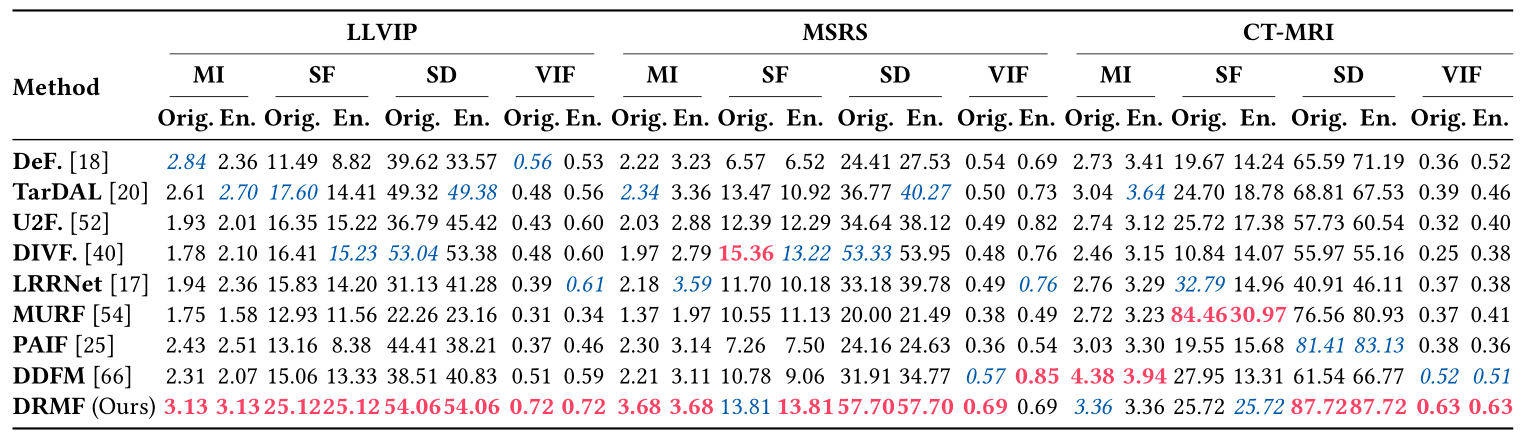
表2. 在挑战性场景中，DRMF与SOTA方法在IVIF和MIF任务上的定量比较。

4.4 扩展实验

低光图像增强

我们验证了我们的DRCDM在低光图像增强（LLIE）这一重要的图像恢复任务上的有效性。DRCDM与几种主流算法进行了比较，包括KinD、ChebyLighter、RUAS、CLIP-LIT、CUE、FourLLIE和DiffLL。一个典型的例子如图4所示。很明显，只有KinD、CUE、DiffLL和DRCDM能够忠实地以自然的亮度渲染场景。值得注意的是，具有强大生成能力的DRCDM可以在黑暗中挖掘信息，如矩形框突出显示的那样。涉及PSNR、SSIM、MUSIQ和LIQE的定量评估呈现在表3中。最好的MUSIQ和LIQE表明DRCDM达到了最佳的感知质量，而较高的PSNR和SSIM则意味着我们的结果与参考图像非常接近。这些发现证明了DRCDM在应对挑战性图像退化方面的能力。LLIE任务上的定性和定量实验共同证明了DRCDM在解决图像退化挑战方面的实用性。

图4. 低光增强的一个应用示例。

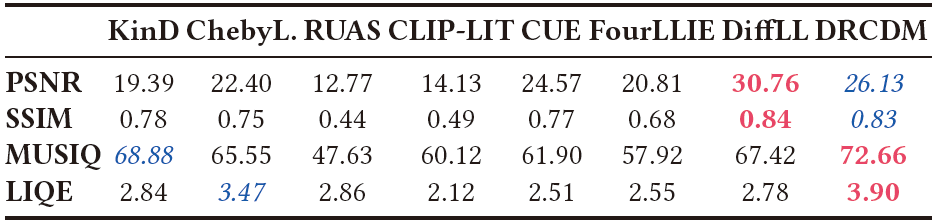
表3. LOL数据集上的定量比较结果。

对其他融合方法的预增强

我们的DRCDM可以直接增强源图像，作为其他融合方法的预处理步骤。图5展示了一些代表性的例子。DRCDM为实际和退化场景都生成了高质量的源图像。当现有的融合方法将增强后的源图像作为输入时，定性和定量结果都显示出显著的改善。例如，VI图像中的背景（如栅栏）和MRI图像中的结构都呈现得更清晰，SD和VIF指标也显著提高。

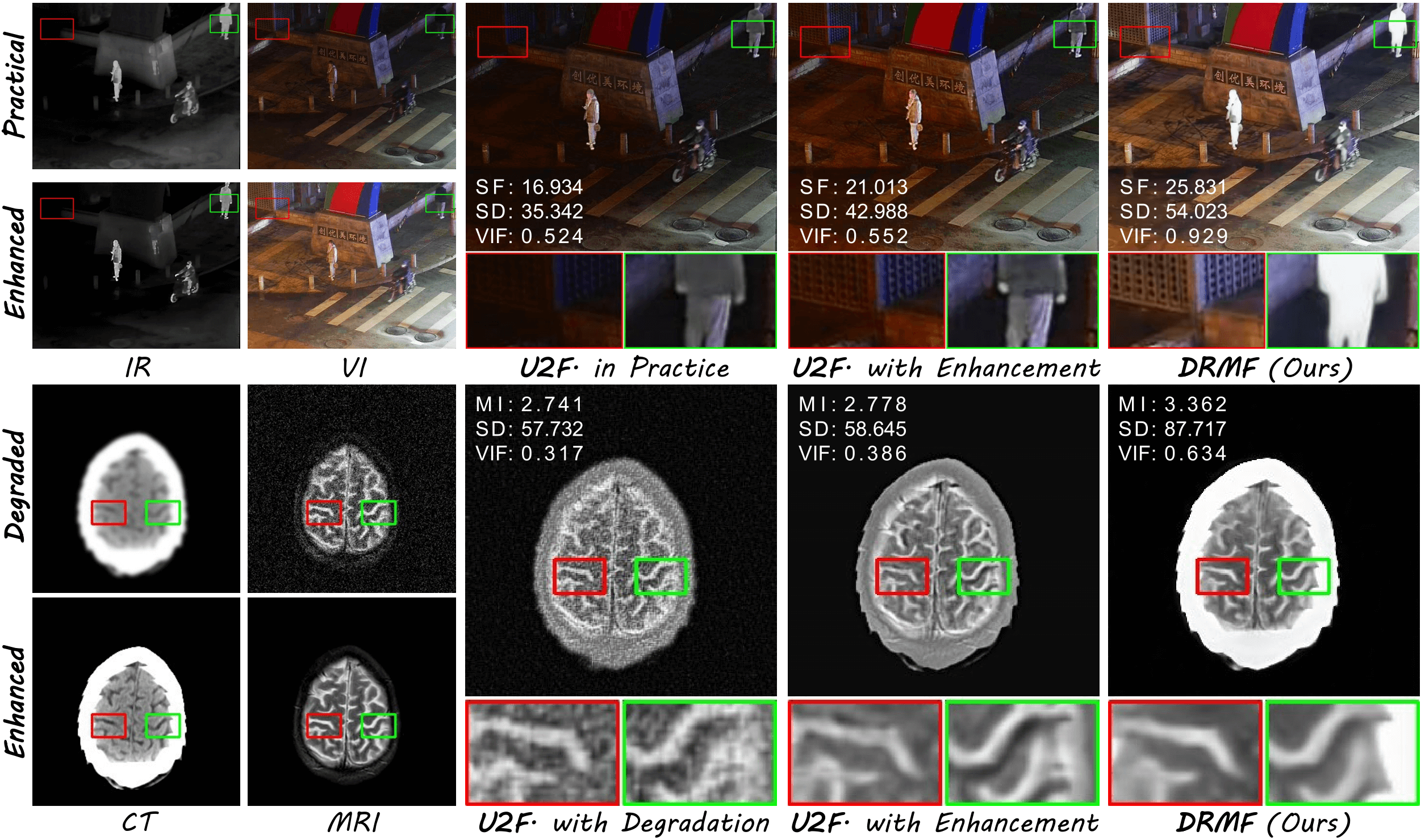
图5. 作为现有方法的预增强方法。

目标检测

有效的信息增强和聚合不仅有助于视觉感知，还能促进机器视觉。因此，我们在LLVIP上评估了目标检测性能，以进一步揭示DRMF的优越性，使用重新训练的YOLO v8作为检测器。在图6中，DRMF在实际和挑战性场景中都检测到了所有行人。相比之下，源图像和其他方法都存在不同程度的漏检。表4显示，DRMF平衡了精确率和召回率，从而实现了更好的平均精度（AP）。特别地，在各种IoU阈值下的最佳平均精度均值（mAP）意味着DRMF可以适应不同的IoU设置。

图6. LLVIP上的目标检测可视化比较结果。

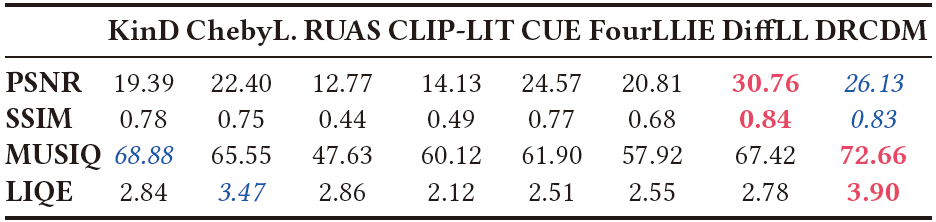
表4. 在LLVIP数据集上的目标检测定量比较结果。

4.5 讨论

计算成本。虽然扩散模型确实增加了计算成本，但我们的DRMF在一个单一的框架内实现了退化处理和融合，与其他“预增强+融合”方案相比，在推理时间上显示出明显的优势，如表5所示。因此，在处理涉及退化的实际场景时，我们的成本是可以接受的。

领域偏移。我们在源模态中预训练DRCDMs，但融合过程涉及融合模态。融合模态和源模态之间存在领域偏移。请注意，在我们的方法中，领域偏移对噪声预测网络和融合性能的影响是可以接受的。图7从另一个角度提供了证据。从$x_{t=7}^{ir}$（或$x_{t=14}^{ir}$）和$x_T^{vi}(T=20)$开始的可见光分支的扩散逆过程产生了相似的结果，尽管$x_{t=7}^{ir}$和$x_{t=7}^{vi}$之间存在明显的领域偏移。此外，融合分布$x_t^f$与其中一个源（即$x_t^{ir}$或$x_t^{vi}$）之间的领域偏移通常小于源分布本身之间的偏移（即$x_t^{ir}$和$x_t^{vi}$），并且它可能足够小，以至于可以为图像生成保留扩散轨迹并保证融合性能。

表5. 计算效率比较。

图7. 领域偏移对扩散过程的影响。

4.6 消融实验

鲁棒条件扩散模型（DRCDM）。DRCDM利用扩散模型强大的生成能力来消除各种退化的影响。如图8©所示，当用一个典型的条件扩散模型替换DRCDM时（该模型提供重构输入的先验），结果忠实于源图像。具体来说，融合后的图像保留了源图像中的共同信息，但未能消除恶劣的退化。如表6所示，更高的MI意味着没有DRCDM提供的先验的融合模型从源图像向融合图像传递了更多的信息。不幸的是，在纹理和视觉质量方面有明显的退化。

扩散先验组合模块（DPCM）。DPCM旨在自适应地整合由不同模态驱动的扩散先验，从而保留关键信息。我们进行了一项消融研究，使用简单的平均加权策略代替DPCM。如图8(d)所示，融合结果倾向于平均增强后的源图像。具体来说，即使有DRCDM提供鲁棒的先验，由于无法自适应地聚合相关先验，融合结果仍然会经历退化。表6中的下降结果也证实了这个问题。相比之下，同时配备了DRCDM和DPCM的DRMF可以有效地应对复杂的退化并保留必要的细节和目标。

图8. 消融研究的可视化比较。

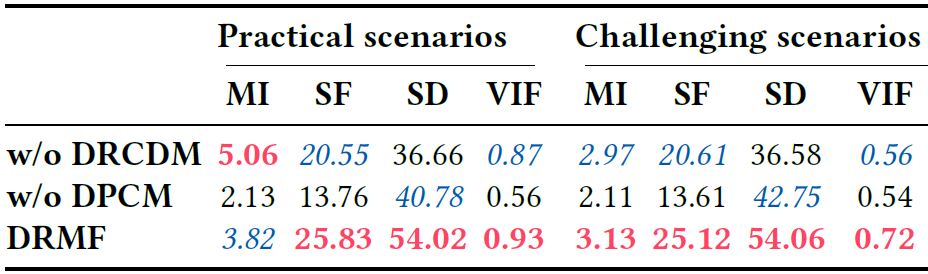
表6. 消融研究的定量比较。

5 结论

这项工作提出了一个基于可组合扩散先验的鲁棒多模态图像融合框架。我们设计了鲁棒条件扩散模型，以消除源图像中不利的退化并提供鲁棒的扩散先验。此外，我们开发了一个扩散先验组合模块，以自适应地聚合由各种模态驱动的扩散先验，并逐步生成融合图像。在IVIF和MIF上的实验证明了我们的方法在实际和挑战性场景中抑制退化和聚合信息方面的优越性。