一、排序算法
插入排序
⒈从有序数列和无序数列{a2,a3，…，an}开始进行排序；
⒉处理第i个元素时（i=2,3，…，n），数列{a1,a2，…，ai-1}是已有序的，而数列{ai,ai+1，…，an}是无序的。用ai与ai-1，a i-2，…，a1进行比较，找出合适的位置将ai插入；
⒊重复第二步，共进行n-i次插入处理，数列全部有序。
#include "stdafx.h"
/*
比较：
每个元素插入到已排序的数组中，每次从数组中拿一个要插入的元素，从数组位置0开始到此元素位置中找到此数据的插入位置，腾出此插入位置
移动：
腾出插入位置时需要移动，移动次数为此元素位置到插入位置之间的距离。
临时变量：
要比较元素位置的整型临时变量
*/
void InsertSortE(int a[],int nInsertVal,int n);
void InsertSort(int src[],int n)
{
for (int i = 0; i < n; ++i)// 将每个数插入到已排序数组中
{
InsertSortE(src,src[i],i);
}
}
void InsertSortE(int a[],int nInsertVal,int n)// 参数n指数组位置坐标最大值，即从0开始
{
int i;
for (i = 0; i < n; ++i)// 从0到n中，找某一元素的插入位置
{
if (nInsertVal < a[i])// 找到插入数组位置
{
for (int j = n; j > i; --j)// 腾出插入位置，腾出数组位置n到i
{
a[j] = a[j-1];
}
break;// 必不可少，找到断点循环应停止
}
}
a[i] = nInsertVal;
}
void PrintArray(int *p,int n)
{
for (int i = 0; i < n; ++i)
{
printf("%d\t",*(p+i));
}
printf("\n");
}
int _tmain(int argc, _TCHAR* argv[])
{
int src[] = {3,1,9,4,56,23,98,0};
printf("转换前：\n");
PrintArray(src,8);
InsertSort(src,8);
printf("转换后:\n");
PrintArray(src,8);
getch();
return 0;
}
冒泡排序
- void bubbleSort(T* a,int n)
- {
- for(int i = 0;i < n - 1;i++)
- {
- for(int j = 0;j < n - i - 1;j++)
- {
- if(a[j] > a[j + 1])
- {
- T temp = a[j];
- a[j] = a[j + 1];
- a[j + 1] = temp;
- }
- }
- }
- }
选择排序
选择排序是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小元素，然后放到排序序列末尾。以此类推，直到所有元素均排序完毕。
选择排序的不稳定性分析：
选择排序每次找剩余未排序元组中的最小值，并和前面的元素交换位置，这样的元素交换破坏了稳定性。例如： 5 8 5 2 9 ，第一次找到的最小元素 2 ，与第一个 5 交换位置，则第一个 5 和中间的 5 顺序就变了，所以不稳定了。
总结：选择排序是原地不稳定排序，平均时间复杂度 O(n2)
- 代码如下：
- //文件selectSort.h
- //选择排序
- template <class T>
- void selectSort(T* a,int n)
- {
- for(int i = 0;i < n - 1;i++)
- {
- //记下最小值(最小值初始为a[i])
- T min = a[i];
- //记下下标
- int k = i;
- for(int j = i + 1;j < n;j++)
- {
- if(a[j] < min)
- {
- min = a[j];
- k = j;
- }
- }
- //交换(当最小值不是第一个的时候)
- if(k != i)
- {
- T temp = a[i];
- a[i] = a[k];
- a[k] = temp;
- }
- }
- }
归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
归并排序是稳定的排序.即相等的元素的顺序不会改变.
int is1[n],is2[n];// 原数组is1，临时空间数组is2，n为个人指定长度
void mergeSort(int a,int b)// 下标，例如数组int is[5]，全部排序的调用为mergeSort(0,4)
{
if(a<b)
{
int mid=(a+b)/2;
mergeSort(a,mid);
mergeSort(mid+1,b);
merge(a,mid,b);
}
}1. void merge(int low,int mid,int high)
2. {
3. int i=low,j=mid+1,k=low;
4. while(i<=mid&&j<=high)
5. if(is1[i]<=is1[j]) // 此处为排序顺序的关键，用小于表示从小到大排序
6. is2[k++]=is1[i++];
7. else
8. is2[k++]=is1[j++];
9. while(i<=mid)
10. is2[k++]=is1[i++];
11. while(j<=high)
12. is2[k++]=is1[j++];
13. for(i=low;i<=high;i++)// 写回原数组
14. is1[i]=is2[i];
15. }
快速排序
设要
排序的
数组是A[0]……A[N-1]，首先任意选取一个数据（通常选用第一个数据）作为关键数据，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面，这个过程称为一趟快速
排序。值得注意的是，快速
排序不是一种稳定的
排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动。
一趟快速
排序的算法是：
2）以第一个
数组元素作为关键数据，赋值给key，即key=A[0]；
3）从j开始向前搜索，即由后开始向前搜索（j -- ），找到第一个小于key的值A[j]，A[i]与A[j]交换；
4）从i开始向后搜索，即由前开始向后搜索（i ++ ），找到第一个大于key的A[i]，A[i]与A[j]交换；
5）重复第3、4、5步，直到 I=J； (3,4步是在程序中没找到时候j=j-1，i=i+1，直至找到为止。找到并交换的时候i， j指针位置不变。另外当i=j这过程一定正好是i+或j-完成的最后令循环结束。）
(6) test
示例
|
A[0]
|
A[1]
|
A[2]
|
A[3]
|
A[4]
|
A[5]
|
A[6]
|
|
49
|
38
|
65
|
97
|
76
|
13
|
27
|
进行第一次交换后：27 38 65 97 76 13 49
( 按照算法的第三步从后面开始找，此时:J=6）
进行第二次交换后：27 38 49 97 76 13 65
( 按照算法的第四步从前面开始找>
key的值，65>49,两者交换，此时：I=2 )
进行第三次交换后：27 38 13 97 76 49 65
( 按照算法的第五步将又一次执行算法的第三步从后开始找
进行第四次交换后：27 38 13 49 76 97 65
( 按照算法的第四步从前面开始找大于
key的值，97>49，两者交换，此时：I=3,J=5 )
此时再执行第三和四步的时候就发现I=J=4，从而结束一趟快速
排序，那么经过一趟快速排序之后的结果是：27 38 13 49 76 97 65，即所有大于
key49的数全部在49的后面，所有小于
key（49）的数全部在
key（49）的前面。
intpartitions(int a[],int low,int high)
{
int pivotkey=a[low];
//a[0]=a[low];
while(low<high)
{
while(low<high && a[high]>=pivotkey)
--high;
a[low]=a[high];
while(low<high && a[low]<=pivotkey)
++low;
a[high]=a[low];
}
//a[low]=a[0];
a[low]=pivotkey;
return low;
}
void qsort(int a[],int low,int high)
{
int pivottag;
if(low<high)
{ //递归调用
pivottag=partitions(a,low,high);
qsort(a,low,pivottag-1);
qsort(a,pivottag+1,high);
}
}
void quicksort(int a[],int n)
{
qsort(a,0,n);
}
//简单示例
#include <stdio.h>
//#include <math.h>
#include "myfunc.h" //存放于个人函数库中
main()
{
int i,a[11]={0,11,12,5,6,13,8,9,14,7,10};
for(i=0;i<11;printf("%3d",a[i]),++i);
printf("\n");
quicksort(a,10);
for(i=0;i<11;printf("%3d",a[i]),++i);
printf("\n");
}
堆排序
堆排序 转自：http://www.cnblogs.com/dolphin0520/archive/2011/10/06/2199741.html
堆排序是利用堆的性质进行的一种选择排序。下面先讨论一下堆。
1.堆
堆实际上是一棵完全二叉树，其任何一非叶节点满足性质：
Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]或者Key[i]>=Key[2i+1]&&key>=key[2i+2]
即任何一非叶节点的关键字不大于或者不小于其左右孩子节点的关键字。
堆分为大顶堆和小顶堆，满足Key[i]>=Key[2i+1]&&key>=key[2i+2]称为大顶堆，满足 Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]称为小顶堆。由上述性质可知大顶堆的堆顶的关键字肯定是所有关键字中最大的，小顶堆的堆顶的关键字是所有关键字中最小的。
2.堆排序的思想
利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。
其基本思想为(大顶堆)：
1)将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆，此堆为初始的无序区；
2)将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n];
3)由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。
操作过程如下：
1)初始化堆：将R[1..n]构造为堆；
2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换，然后将新的无序区调整为新的堆。
因此对于堆排序，最重要的两个操作就是构造初始堆和调整堆，其实构造初始堆事实上也是调整堆的过程，只不过构造初始堆是对所有的非叶节点都进行调整。
下面举例说明：
给定一个整形数组a[]={16,7,3,20,17,8}，对其进行堆排序。
首先根据该数组元素构建一个完全二叉树，得到
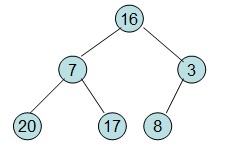
20和16交换后导致16不满足堆的性质，因此需重新调整
这样就得到了初始堆。
即每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质，因此每次交换之后要重新对被交换的孩子节点进行调整)。有了初始堆之后就可以进行排序了。
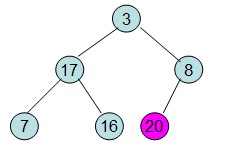此时3位于堆顶不满堆的性质，则需调整继续调整
这样整个区间便已经有序了。
从上述过程可知，堆排序其实也是一种选择排序，是一种树形选择排序。只不过直接选择排序中，为了从R[1...n]中选择最大记录，需比较n-1次，然后从R[1...n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过，而树形选择排序恰好利用树形的特点保存了部分前面的比较结果，因此可以减少比较次数。对于n个关键字序列，最坏情况下每个节点需比较log2(n)次，因此其最坏情况下时间复杂度为nlogn。堆排序为不稳定排序，不适合记录较少的排序。
测试程序
/*堆排序(大顶堆) 2011.9.14*/ #include <iostream> #include<algorithm> using namespace std; void HeapAdjust(int *a,int i,int size) //调整堆 { int lchild=2*i; //i的左孩子节点序号 int rchild=2*i+1; //i的右孩子节点序号 int max=i; //临时变量 if(i<=size/2) //如果i是叶节点就不用进行调整 { if(lchild<=size&&a[lchild]>a[max]) { max=lchild; } if(rchild<=size&&a[rchild]>a[max]) { max=rchild; } if(max!=i) { swap(a[i],a[max]); HeapAdjust(a,max,size); //避免调整之后以max为父节点的子树不是堆 } } } void BuildHeap(int *a,int size) //建立堆 { int i; for(i=size/2;i>=1;i--) //非叶节点最大序号值为size/2 { HeapAdjust(a,i,size); } } void HeapSort(int *a,int size) //堆排序 { int i; BuildHeap(a,size); for(i=size;i>=1;i--) { //cout<<a[1]<<" "; swap(a[1],a[i]); //交换堆顶和最后一个元素，即每次将剩余元素中的最大者放到最后面 //BuildHeap(a,i-1); //将余下元素重新建立为大顶堆 HeapAdjust(a,1,i-1); //重新调整堆顶节点成为大顶堆 } } int main(int argc, char *argv[]) { //int a[]={0,16,20,3,11,17,8}; int a[100]; int size; while(scanf("%d",&size)==1&&size>0) { int i; for(i=1;i<=size;i++) cin>>a[i]; HeapSort(a,size); for(i=1;i<=size;i++) cout<<a[i]<<""; cout<<endl; } return 0; }
希尔排序
希尔排序基本思想：
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分成d1个组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行
直接插入排序
；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量dt=1(dt<dt-l<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。
该方法实质上是一种分组插入方法。
给定实例的shell排序的排序过程
假设待排序文件有10个记录，其关键字分别是：
49，38，65，97，76，13，27，49，55，04。
增量序列的取值依次为：
5，3，1
缩小增量法
属于插入类排序,是将整个无序列分割成若干小的子序列分别进行插入排序
排序过程：先取一个正整数d1<n，把所有序号相隔d1的数组元素放一组，组内进行直接插入排序；然后取d2<d1，重复上述分组和排序操作；直至di=1，即所有记录放进一个组中排序为止
初始：d=5
49 38 65 97 76 13 27 49* 55 04
49 13
|-------------------|
38 27
|-------------------|
65 49*
|-------------------|
97 55
|-------------------|
76 04
|-------------------|
一趟结果
13 27 49* 55 04 49 38 65 97 76
d=3
13 27 49* 55 04 49 38 65 97 76
13 55 38 76
|------------|------------|------------|
27 04 65
|------------|------------|
49* 49 97
|------------|------------|
二趟结果
13 04 49* 38 27 49 55 65 97 76
d=1
13 04 49* 38 27 49 55 65 97 76
|----|----|----|----|----|----|----|----|----|
三趟结果
04 13 27 38 49* 49 55 65 76 97
--------------------------------------------------------------------------------------------
例如对503,17,512,908,170,897,275,653,462，154，509，612，677，765，703，94排序的C++语言算法
算法思想简单描述：
在直接插入排序算法中，每次插入一个数，使有序序列只增加1个节点，
并且对插入下一个数没有提供任何帮助。如果比较相隔较远距离（称为
增量）的数，使得数移动时能跨过多个元素，则进行一次比较就可能消除
多个元素交换。D.L.shell于1959年在以他名字命名的排序算法中实现
了这一思想。算法先将要排序的一组数按某个增量d分成若干组，每组中
记录的下标相差d.对每组中全部元素进行排序，然后再用一个较小的增量
对它进行，在每组中再进行排序。当增量减到1时，整个要排序的数被分成
一组，排序完成。
下面的函数是一个希尔排序算法的一个实现，初次取序列的一半为增量，
以后每次减半，直到增量为1。
希尔排序是不稳定的。
#include<iostream>
using namespace std;
void HealSort(int *a,int length)
{
int b[1000]={0};
int k=length/2;
int i,j,temp;
while(k>0)
{
for(i=0;i<length-k;i++)
{
j=k+i;
while(j>=k) //小组内排序，以j递减的k的方式，从小组头开始排序，后面再添加组员进来，依次向前比较，插入到合适的位置。
{
if(a[j]<a[j-k])
{
temp=a[j];
a[j]=a[j-k];
a[j-k]=temp;
j=j-k;
}
else
break;
}
}
k=k/2;
}
}
int main()
{
int a[10]={15,6,28,89,61,92,43,24,47,510};
HealSort(a,10);
for(int i=0;i<10;i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
system("pause");
return 0;
}算法分析
优劣
不需要大量的辅助空间，和归并排序一样容易实现。希尔排序是基于插入排序的一种算法， 在此算法基础之上增加了一个新的特性，提高了效率。希尔排序的时间复杂度为 O(N*(logN)2)， 没有快速排序算法快 O(N*(logN))，因此中等大小规模表现良好，对规模非常大的数据排序不是 最优选择。但是比O(N2）复杂度的算法快得多。并且希尔排序非常容易实现，算法代码短而简单。 此外，希尔算法在最坏的情况下和平均情况下执行效率相差不是很多，与此同时快速排序在最坏 的情况下执行的效率会非常差。 专家们提倡，几乎任何排序工作在开始时都可以用希尔排序，若在实际使用中证明它不够快， 再改成快速排序这样更高级的排序算法. 本质上讲，希尔排序算法的一种改进，减少了其复制的次数，速度要快很多。 原因是，当N值很大时数据项每一趟排序需要的个数很少，但数据项的距离很长。 当N值减小时每一趟需要和动的数据增多，此时已经接近于它们排序后的最终位置。 正是这两种情况的结合才使希尔排序效率比插入排序高很多。
时间性能
1．增量序列的选择
Shell排序的执行时间依赖于增量序列。
好的增量序列的共同特征：
① 最后一个增量必须为1；
② 应该尽量避免序列中的值(尤其是相邻的值)互为倍数的情况。
有人通过大量的实验，给出了目前较好的结果：当n较大时，比较和移动的次数约在nl.25到1.6n1.25之间。
2．Shell排序的时间性能优于直接插入排序
希尔排序的时间性能优于直接插入排序的原因：
①当文件初态基本有序时直接插入排序所需的比较和移动次数均较少。
②当n值较小时，n和n2的差别也较小，即直接插入排序的最好时间复杂度O(n)和最坏时间复杂度0(n2)差别不大。
③在希尔排序开始时增量较大，分组较多，每组的记录数目少，故各组内直接插入较快，后来增量di逐渐缩小，分组数逐渐减少，而各组的记录数目逐渐增多，但由于已经按di-1作为距离排过序，使文件较接近于有序状态，所以新的一趟排序过程也较快。
因此，希尔排序在效率上较直接插人排序有较大的改进。
稳定性
排序前一个序列中,如果出现N个与关键字相同的数据,那么排序后仍然按照原先序列的排列顺序排列,就说这个算法是稳定的,反之就是不稳定的。通俗地讲就是能保证排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。在简单形式化一下，如果Ai = Aj, Ai原来在位置前，排序后Ai还是要在Aj位置前。
希尔分析
希尔排序是按照不同步长对元素进行插入排序，当刚开始元素很无序的时候，步长最大，所以插入排序的元素个数很少，速度很快；当元素基本有序了，步长很小，插入排序对于有序的序列效率很高。所以，希尔排序的时间复杂度会比o(n^2)好一些。由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的
/********************************************************************************************************/
逆序：
字符串逆序：http://www.cnblogs.com/graphics/archive/2011/03/09/1977717.html
原地逆序
英文叫做in-place reverse。这是最常考的，原地逆序意味着不允额外分配空间，主要有以下几种方法，思想都差不多，就是将字符串两边的字符逐个交换，如下图。给定字符串"abcdef"，逆序的过程分别是交换字符a和f，交换字符b和e，交换字符c和d。
一 设置两个指针，分别指向字符串的头部和尾部，然后交换两个指针所指的字符，并向中间移动指针直到交叉。
char* Reverse(char* s)
{
// p指向字符串头部
char* p = s ;
// q指向字符串尾部
char* q = s ;
while( *q )
++q ;
q -- ;
// 交换并移动指针，直到p和q交叉
while(q > p)
{
char t = *p ;
*p++ = *q ;
*q-- = t ;
}
return s ;
}
二 用递归的方式，需要给定逆序的区间，调用方法:Reverse(s, 0, strlen(s)) ;
// 对字符串s在区间left和right之间进行逆序，递归法
void Reverse( char* s, int left, int right )
{
if(left >= right)
return s ;
char t = s[left] ;
s[left] = s[right] ;
s[right] = t ;
Reverse(s, left + 1, right - 1) ;
}三 非递归法，同样指定逆序区间，和方法一没有本质区别，一个使用指针，一个使用下标。
// 对字符串str在区间left和right之间进行逆序
char* Reverse( char* s, int left, int right )
{
while( left < right )
{
char t = s[left] ;
s[left++] = s[right] ;
s[right--] = t ;
}
return s ;
}不允许临时变量的原地逆序
使用异或操作
// 使用异或操作对字符串s进行逆序
char* Reverse(char* s)
{
char* r = s ;
//令p指向字符串最后一个字符
char* p = s;
while (*(p + 1) != '\0')
++p ;
// 使用异或操作进行交换
while (p > s)
{
*p = *p ^ *s ;
*s = *p ^ *s ;
*p = *p-- ^ *s++ ;
}
return r ;
}
按单词逆序
给定一个字符串，按单词将该字符串逆序，比如给定"This is a sentence"，则输出是"sentence a is This"，为了简化问题，字符串中不包含标点符号。
分两步
1 先按单词逆序得到"sihT si a ecnetnes"
2 再整个句子逆序得到"sentence a is This"
对于步骤一，关键是如何确定单词，这里以空格为单词的分界。当找到一个单词后，就可以使用上面讲过的方法将这个单词进行逆序，当所有的单词都逆序以后，将整个句子看做一个整体（即一个大的包含空格的单词）再逆序一次即可，如下图所示，第一行是原始字符换，第二行是按单词逆序后的字符串，最后一行是按整个句子逆序后的字符串。
代码
// 对指针p和q之间的所有字符逆序
void ReverseWord(char* p, char* q)
{
while(p < q)
{
char t = *p ;
*p++ = *q ;
*q-- = t ;
}
}
// 将句子按单词逆序
char* ReverseSentence(char* s)
{
// 这两个指针用来确定一个单词的首尾边界
char* p = s ; // 指向单词的首字符
char* q = s ; // 指向空格或者 '\0'
while(*q != '\0')
{
if (*q == '')
{
ReverseWord(p, q - 1) ;
q++ ; // 指向下一个单词首字符
p = q ;
}
else
q++ ;
}
ReverseWord(p, q - 1) ; // 对最后一个单词逆序
ReverseWord(s, q - 1) ; // 对整个句子逆序
return s ;
}逆序打印
还有一类题目是要求逆序输出，而不要求真正的逆序存储。这题很简单，有下面几种方法，有的方法效率不高，这里仅是提供一个思路而已。
先求出字符串长度，然后反向遍历即可。
void
ReversePrint(
const
char
*
s)
{
int len = strlen(s) ;
for ( int i = len - 1 ; i >= 0 ; -- i)
cout << s[i];
}
{
int len = strlen(s) ;
for ( int i = len - 1 ; i >= 0 ; -- i)
cout << s[i];
}
如果不想求字符串的长度，可以先遍历到末尾，然后在遍历回来，这要借助字符串的结束符'\0
void ReversePrint(const char* s) { const char* p = s ; while (*p) *p++ ; --p ; //while结束时，p指向'\0'，这里让p指向最后一个字符 while (p >= s) { cout <<*p ; --p ; } }
对于上面第二种方法，也可以使用递归的方式完成。
void
ReversePrint(
const
char
*
s)
{
if ( * (s + 1 ) != ' \0 ' )
ReversePrint(s + 1 ) ;
cout << * s ;
}
{
if ( * (s + 1 ) != ' \0 ' )
ReversePrint(s + 1 ) ;
cout << * s ;
}
查找子串
/*参考代码*/
/* Programming Exercise 11-7 */
#include <stdio.h>
#define LEN 20
char * string_in(const char * s1, const char * s2);
int main(void)
{
char orig[LEN] = "transportation";
char * find;
puts(orig);
find = string_in(orig, "port");
if (find)
puts(find);
else
puts("Not found");
find = string_in(orig, "part");
if (find)
puts(find);
else
puts("Not found");
getch();
return 0;
}
#include <string.h> /*此函数中有些地方不明，请加以指点，谢谢！*/
char * string_in(const char * s1, const char * s2)
{
int l2 = strlen(s2); /* 这部分是何用意？成立吗？*/
int tries; /* maximum number of comparisons */
int nomatch = 1; /* set to 0 if match is found */
tries = strlen(s1) + 1 - l2; /*此部分有何作用？*/
if (tries > 0)
while (( nomatch = strncmp(s1, s2, l2)) && tries--)
s1++;
if (nomatch)
return NULL;
else
return (char *) s1; /* cast const away */
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
