如果你是与JAVA相关方向的,可以看看这篇文章,相信对你会有所帮助: 点击打开链接
算法(第四版) 第12次印刷
感觉我真的是良心博主。。。。
注意!!! :书上的过程图有些是比较坑的(非错误问题),比如P525的NFA并不是只执行了构造函数后的结果而是将构造函数和该类中的一个方法一起运行后的结果,比较坑,如果对书中算法有什么不懂的可以看看我写的注释(在Algorithms中),如果没有注释的要么是没必要,要么就是我也不会(比如红黑树的删除部分)
关于终止Console继续读入流:
书上有一些题目需要从console读取流并进行处理(我之前的代码都是直接用In类和命令行参数代替了),从console读取有个问题就是如何终止流的输入,如果不手动终止输入StdIn.isEmpty始终是false,这样后面的代码始终无法执行,Eclipse默认的EOF是ctrl+Z(在console输入完内容按完回车以后按ctrl+z(在console中)就会终止当前输入,StdIn.isEmpty为true),有个尴尬的问题是ctrl+z经常是无效的即你按了ctrl+z也不能终止流的输入,一开始我以为是快捷键的冲突导致的,结果改了以后仍是无效的,但我发现每次第一次启动eclipse后用ctrl+z终止流输入时有效的再次运行那个类就失效了,因此我想到的就是每次运行过一次以后就刷新(eclipse最左边建工程的地方点鼠标右键)要注意一点,你刷新的时候一定要选定那个类不要点在别的类刷新,这样是没用的,再次运行时EOF有效(可能会出现刷新一次后EOF仍然失效,再次刷新一次即可,在刷新之前一定要把当前运行的类终止,即console中红色的小正方形点一下变灰色)
参考代码:点击打开链接
Eclipse从控制台直接读取文件:
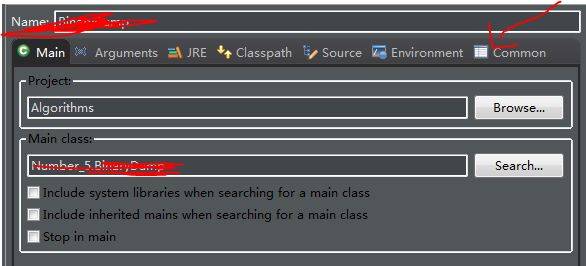
比如你运行的类当前需要读取一个.txt的文件,而你不向想通过将内容复制到concole中读取或者通过命令行参数读取,而是想直接通过控制台读取并使用相应的方法,则可以通过这样设置达到目的:Run---->Run configurations--->
这样点击运行的时候控制台什么都不要输入,直接EOF(不会看第一条),在读取比特流的时候采用console读取具体数据和从控制台直接读取.txt文件时有区别的,具体区别见下面的参考代码里的注释,这是针对数据压缩那里的内容,前面的自行测试
参考代码:点击打开链接
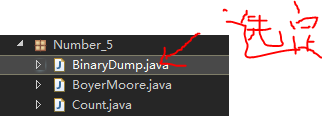
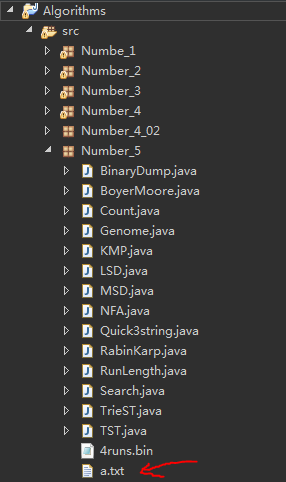
针对第五章第五节数据压缩算法的测试,基本思路将output定向到一个.txt文件中(如何定向看第二条),将压缩后的比特流保存到一个.txt的文件中,验证解压缩算法时,从.txt文件中读取比特流然后在控制台打印解压后的内容,具体操作看下面的图:首先新建一个用于保存比特流的.txt文件,我这里是a.txt,将文件放入具体的包中,
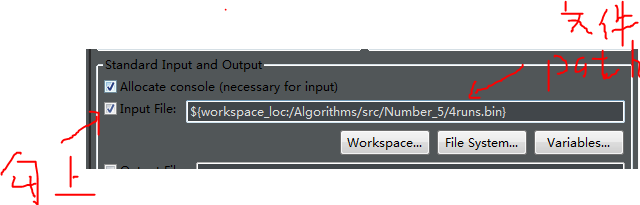
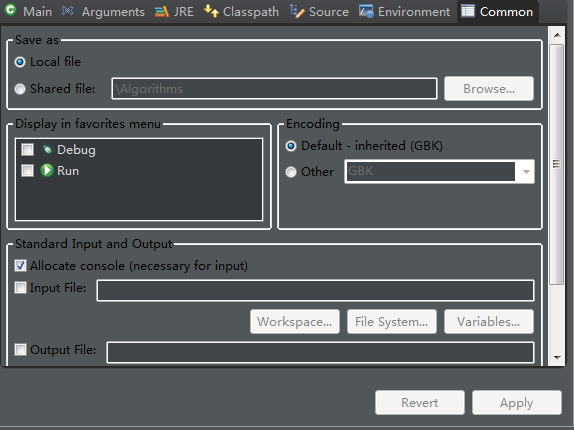
然后将输出定向到该文件(看第二条),输出路径的设置:
首先先点inputfile通过workspace找到a.txt这个文件,这时候将inputfule的路径复制下来作为outputfile的路径,取消inputfile前面的勾,在outputfile前面打勾,然后apply,直接运行,这样压缩后的比特流就保存到了a.txt文件中(会提示你刷新,刷新一下就行了),验证解压缩算法的时候就是将inputfile定向到a.txt文件
参考代码:点击打开链接
eclipse命令行参数使用:
Run---->Run configurations----->右边 arguments 里写
用空白字符区别不同的命令行参数:
如:1 2 3 args.length=3
123 args.length=1
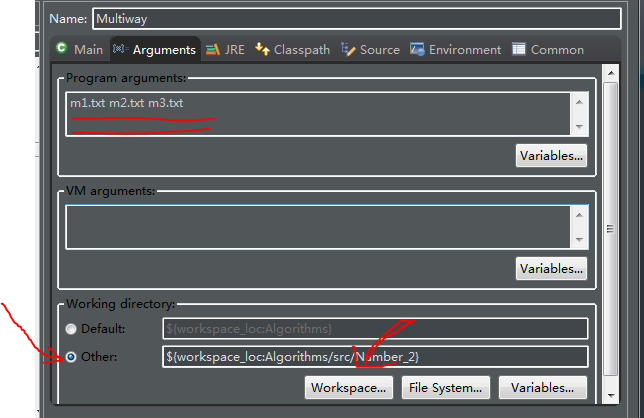
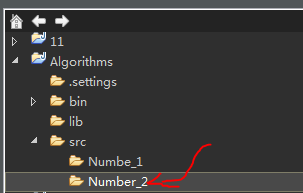
在命令行参数中读取测试用例 xxx.txt ,使用作者提供的jar包,参考书中205 我写的Algorithms/Number_2/Multiway
比如我把 测试用例 m1.txt m2.txt m3.txt拷到了包Number_2下 则只需修改 working directory 为Number_2
贴上我的GitHub地址,习题答案就在里面:
https://github.com/xiaoyuzdy/Algorithms
过几个月打算去找实习,题目会一直写,如果对你有帮助,觉得还不错,并且有github账户,麻烦给我个Star,这对我找工作很有帮助,十分感谢
其中 Algorithms 为书中的一些算法还有就是一些作者自己写的API的使用
AlgorithmsTest 为书中课后习题
TestCase.zip 为书中需要用到的测试用例可使用迅雷下载
再贴上GitHub上一个人写的:
https://github.com/aistrate/AlgorithmsSedgewick/tree/master/1-Fundamentals





















 1446
1446

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








