HDU6231 K-th Number

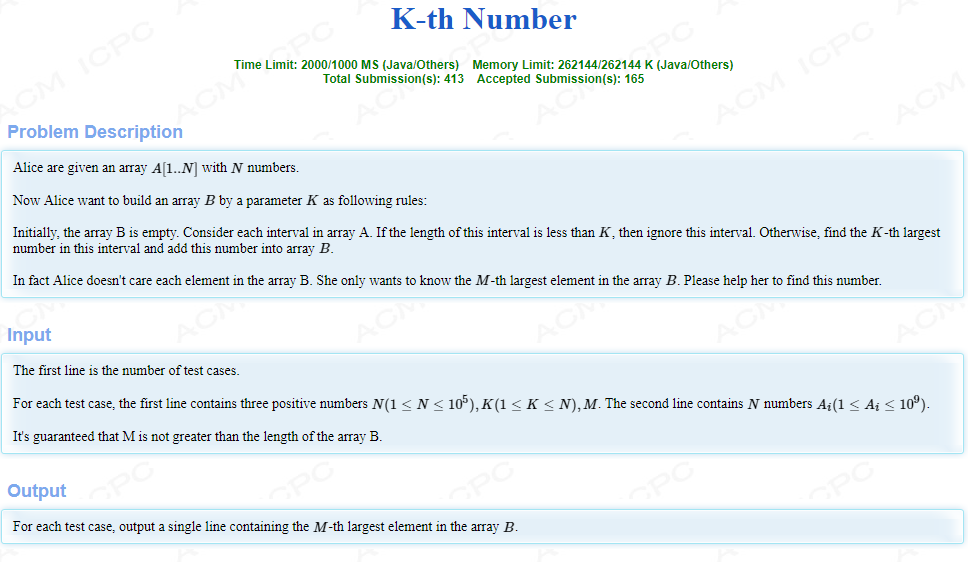
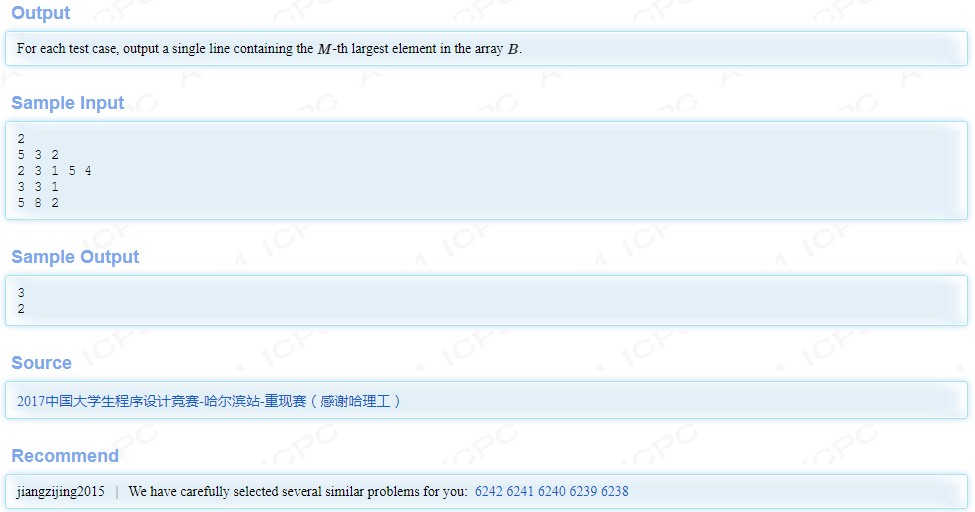
给定一个长为n的序列,对于每个长度大于等于k的区间,取出其第k大的元素,问所有取出的元素中,第m大的那个是多少

考虑二分答案x，则问题转化为求是否有不少于m个区间满足：不少于k个数大于等于x。

考虑使用尺取法做这个判断。

枚举左端点l，找出一个最小的r使其满足条件，则[r,n]中所有点都是符合条件的右端点。由于r的选择具有单调性，我们就可以在O（n）的时间内完成判断。

复杂度O(n*log)

（突然感觉改了个码风也挺好（gui）看（chu）？）

#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int N=1e5+10;

LL m;
int n,k,cas,a[N];

int Check(int mid){
	int l=1,r=1,sum=(a[1]>=mid);
	LL ans=0;
	while (1){
		if (sum>=k){
			ans+=n-r+1;
			sum-=(a[l++]>=mid);
		}
		else{
			sum+=(a[++r]>=mid);
		}
		if (r>n) break;
	}
	return ans>=m;
}

void Solve(){
	scanf("%d%d%lld",&n,&k,&m);
	for (int i=1;i<=n;i++) scanf("%d",&a[i]);
	int l=1,r=1e9;
	while (l<r){
		int mid=(l+r+1)>>1;
		if (Check(mid)) l=mid;
		else r=mid-1;
	}
	printf("%d\n",l);
}

int main(){
	scanf("%d",&cas);
	while (cas--) Solve();
	return 0;
}