#include <iostream>
#include <cstdio>
using namespace std;
int quick(int a, int k ,int mod ){
int ans = 1 ;
while(k){
if(k&1) {
ans = (ans*a)%mod ;
}
a *= a;
a %= mod ;
k >>=1 ;
}
return ans ;
}
int& gcd(int a,int b){
return b==0?a:gcd(b,a%b) ;
}
int main(){
int a , n , m , k ,t ;
cin >> t;
while(t--){
cin >> a >> n >> m >>k ;
cout << (quick(a,gcd(n,m),k)-1+k)%k << endl;
}
return 0 ;
}
Prove that for a≥2, GCD(a^m -1,a^n -1)=a^(GCD(m,n))-1?
#include <iostream>
#include <cstdio>
using namespace std;
int quick(int a, int k ,int mod ){
int ans = 1 ;
while(k){
if(k&1) {
ans = (ans*a)%mod ;
}
a *= a;
a %= mod ;
k >>=1 ;
}
return ans ;
}
int& gcd(int a,int b){
return b==0?a:gcd(b,a%b) ;
}
int main(){
int a , n , m , k ,t ;
cin >> t;
while(t--){
cin >> a >> n >> m >>k ;
cout << (quick(a,gcd(n,m),k)-1+k)%k << endl;
}
return 0 ;
}
any help is appreciated! thanks :)
Answers
Best Answer:
Let g = GCD(a^m - 1, a^n - 1) and let d = GCD(m,n). Then d | m and d | n. Since a^d ≣ 1 (mod a^d - 1),
a^m - 1 = (a^d)^(m/d) - 1 ≣ 1^(m/d) - 1 ≣ 0 (mod a^d - 1)
and
a^n - 1 = (a^d)^(n/d) - 1 ≣ 1^(n/d) - 1 ≣ 0 (mod a^d - 1),
i.e., (a^d - 1) | (a^m - 1) and (a^d - 1) | (a^n - 1). Thus (a^d - 1) | g.
On the other hand, since g = GCD(a^m - 1, a^n - 1), g | (a^m - 1) and g | (a^n - 1). So a^m ≣ 1 (mod g) and a^n ≣ 1 (mod g). Since d = GCD(m,n), there are integers s and t such that d = ms + nt. Thus
a^d - 1 = a^(ms + nt) - 1 = (a^m)^s (a^n)^t - 1 ≣ 1^s * 1^t - 1 ≣ 0 (mod g),
i.e., g | (a^d - 1). Since (a^d - 1) | g as well, we deduce g = a^d - 1.
a^m - 1 = (a^d)^(m/d) - 1 ≣ 1^(m/d) - 1 ≣ 0 (mod a^d - 1)
and
a^n - 1 = (a^d)^(n/d) - 1 ≣ 1^(n/d) - 1 ≣ 0 (mod a^d - 1),
i.e., (a^d - 1) | (a^m - 1) and (a^d - 1) | (a^n - 1). Thus (a^d - 1) | g.
On the other hand, since g = GCD(a^m - 1, a^n - 1), g | (a^m - 1) and g | (a^n - 1). So a^m ≣ 1 (mod g) and a^n ≣ 1 (mod g). Since d = GCD(m,n), there are integers s and t such that d = ms + nt. Thus
a^d - 1 = a^(ms + nt) - 1 = (a^m)^s (a^n)^t - 1 ≣ 1^s * 1^t - 1 ≣ 0 (mod g),
i.e., g | (a^d - 1). Since (a^d - 1) | g as well, we deduce g = a^d - 1.
http://math.stackexchange.com/questions/7473/prove-that-gcdan-1-am-1-a-gcdn-m-1
定理:设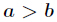 ,
,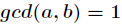 ,那么
,那么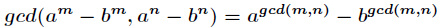
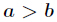 ,
,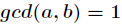 ,那么
,那么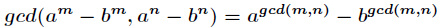






















 1614
1614

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








