ON-LSTM：用有序神经元表达层次结构-CSDN博客

本文转载自 苏剑林[1]在科学空间上关于ON-LSTM非常好的解析, 中间加入一些细节的说明, 以期读者在理解原理之余, 对其实现也有概念. 下面开始…

前言

今天介绍一个有意思的LSTM变种：ON-LSTM，其中“ON”的全称是“Ordered Neurons”，即有序神经元，换句话说这种LSTM内部的神经元是经过特定排序的，从而能够表达更丰富的信息。ON-LSTM来自文章《Ordered Neurons: Integrating Tree Structures into Recurrent Neural Networks》，顾名思义，将神经元经过特定排序是为了将层级结构（树结构）整合到LSTM中去，从而允许LSTM能自动学习到层级结构信息。这篇论文还有另一个身份：ICLR 2019的两篇最佳论文之一(不知道是不是跟作者来自Mila有关系…)，这表明在神经网络中融合层级结构（而不是纯粹简单地全向链接）是很多学者共同感兴趣的课题。

笔者留意到ON-LSTM是因为机器之心的介绍，里边提到它除了提高了语言模型的效果之外，甚至还可以无监督地学习到句子的句法结构！正是这一点特性深深吸引了我，而它最近获得ICLR 2019最佳论文的认可，更是坚定了我要弄懂它的决心。认真研读、推导了差不多一星期之后，终于有点眉目了，遂写下此文。

在正式介绍ON-LSTM之后，我忍不住要先吐槽一下这篇文章实在是写得太差了，将一个明明很生动形象的设计，讲得异常晦涩难懂，其中的核心是 $\tilde{f_{t}}$ 和 $\tilde{i_{t}}$ 的定义，文中几乎没有任何铺垫就贴了出来，也没有多少诠释，开始的读了好几次仍然像天书一样…总之，文章写法实在不敢恭维～

1. 背景: 回顾LSTM

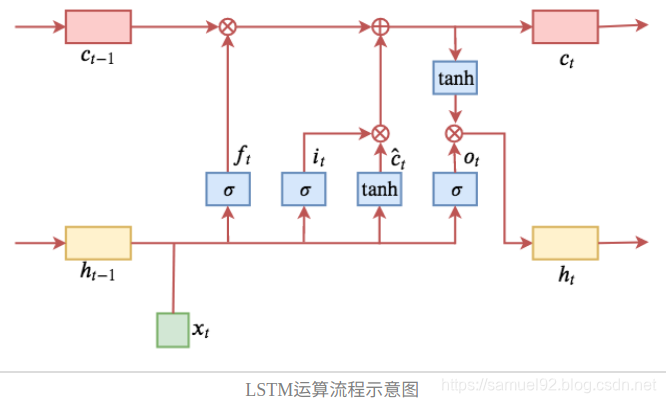
首先来回顾一下普通的LSTM(不考虑层数)。用常见的记号，普通的LSTM写为：

在这里插入图片描述

如果熟悉了神经网络本身，其实这样的结构没有什么神秘的， $f_{t}$ , $i_{t}$ , $o_{t}$ 就是三个单层全连接模型，输入是历史信息 $h_{t−1}$ 和当前信息 $x_{t}$ ，用sigmoid激活，因为sigmoid的结果在0～1之间，所以它们的含义可以诠释为“门（gate）”，分别称为遗忘门、输入门、输出门。不过我个人觉着gate这个名字是不够贴切的，“valve（阀门）”也许更贴切些。

有了门之后， $x_{t}$ 被整合为 $\hat{c_{t}}$ ，然后通过∘运算（对应逐位相乘，有时候也记为⊗）与前面的“门”结合起来，来对 $c_{t−1}$ 和 $\hat{c_{t}}$ 进行加权求和。

Notice: 这里, 相比最一般的RNN(SimpleRNN), LSTM在层间传递中多了一个细胞状态( $c_{t}$ )[2]:

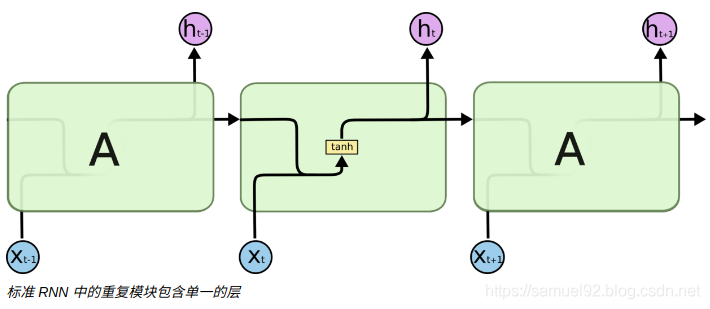
在这里插入图片描述

下图是原博主绘制的图, 可以看到相比RNN, LSTM在层内传递(同一层不同时间步)的时候多了一个细胞状态( $c_{t}$ )[2].

在这里插入图片描述

2. 背景: 语言和序信息

在常见的神经网络中，神经元通常都是无序的，比如遗忘门 $f_t$ 是一个向量，向量的各个元素的位置没有什么规律。如果把LSTM运算过程中涉及到的所有向量的位置按照同一方式重新打乱，权重的顺序也相应地打乱，然后输出结果可以只是原来向量的重新排序（考虑多层的情况下，甚至可以完全不变），信息量不变，不影响后续网络对它的使用。

换言之，LSTM以及普通的神经网络都没有用到神经元的序信息，ON-LSTM则试图把这些神经元排个序，并且用这个序来表示一些特定的结构，从而把神经元的序信息利用起来。

ON-LSTM的思考对象是自然语言。一个自然句子通常能表示为一些层级结构，这些结构如果人为地抽象出来，就是我们所说的语法信息，而ON-LSTM希望能够模型在训练的过程中自然地学习到这种层级结构，并且训练完成后还能把它解析出来（可视化），这就利用到了前面说的神经元的序信息。（曾经做过的相关研究《最小熵原理（三）：“飞象过河”之句模版和语言结构》[3]）

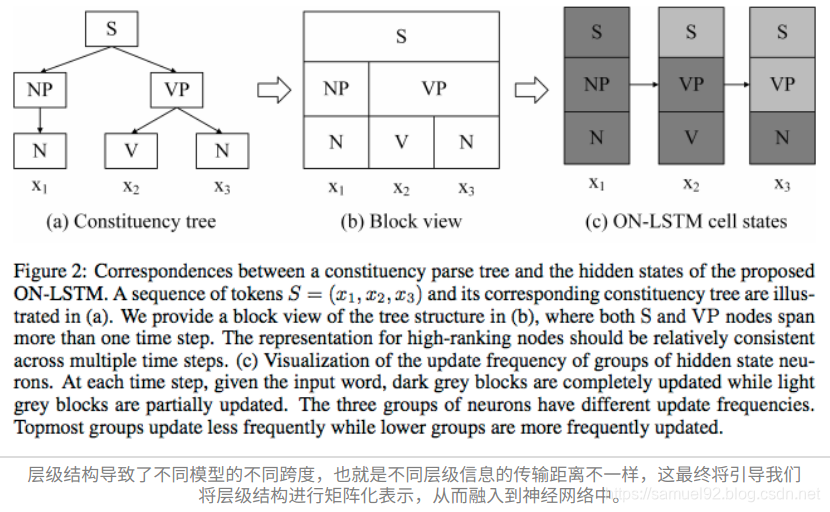
为了达到这个目标，我们需要有一个层级的概念，层级越低代表语言中颗粒度越小的结构，而层级越高则代表颗粒度越粗的结构，比如在中文句子中，“字”可以认为是最低层级的结构，词次之，再上面是词组、短语等。层级越高，颗粒度越粗，那么它在句子中的跨度就越大。
在这里插入图片描述
用原文的图示就是：

3. ON-LSTM

上面的最后一句“层级越高，颗粒度越粗，那么它在句子中的跨度就越大”很容易理解，但它对于ON-LSTM的设计有着指导作用。

首先，这要求我们在设计ON-LSTM的编码时能区分高低层级的信息；其次，这也告诉我们，高层级的信息意味着它要在高层级对应的编码区间保留更久（不那么容易被遗忘门过滤掉），而低层级的信息则意味着它在对应的区间更容易被遗忘。

3.1 设计：分区间更新

有了这个指导之后，我们可以着手建立。假设ON-LSTM中的神经元都排好序后，向量 $c_t$ 的index越小的元素，表示越低层级的信息，而index越大的元素，则表示越高层级的信息。然后，ON-LSTM的门结构和输出结构依然和普通的LSTM一样：
在这里插入图片描述
相比正常的LSTM, ON-LSTM的核心就在于: $\hat{c_{t}}$ 到 $c_{t}$ 的更新方式变化了.

接下来，初始化一个全零的 $c_{t}$ ，即没有任何记忆，或者想象为一个空的U盘。然后，我们将历史信息和当前输入按一定规律存入到 $c_{t}$ 中（即更新 $c_{t}$ ）。每次在更新 $c_{t}$ 之前，首先预测两个整数 $d_f$ : 表示历史信息 $h_{t−1}$ 的层级; $d_i$ : 表示当前输入 $x_{t}$ 的层级：
在这里插入图片描述
至于 $F_1$ , $F_2$ 的具体结构，我们后面再补充，先把核心思路讲清楚。这便是我不满原论文写作的原因，一上来就定义cumax，事前事后都没能把思想讲清楚。

现在我们有了 $d_f$ 和 $d_i$ , 那么作者根据其大小关系, 有两种进行细胞状态的更新的策略.

在这里插入图片描述

至此，我们能够理解ON-LSTM的基本原理了: 它将神经元排序之后，通过位置的前后来表示信息层级的高低，然后在更新神经元时，先分别预测历史的层级 $d_f$ 和输入的层级 $d_i$ ，通过这两个层级来对神经元实行分区间更新。

在这里插入图片描述
这样一来，高层信息就可能保留相当长的距离（因为高层直接复制历史信息，导致历史信息可能不断被复制而不改变），而低层信息在每一步输入时都可能被更新（因为低层直接复制输入，而输入是不断改变的），所以就通过信息分级来嵌入了层级结构。更通俗地说就是分组更新，更高的组信息传得更远（跨度更大），更低的组跨度更小，这些不同的跨度就形成了输入序列的层级结构。

（请反复阅读这段话，必要时对照上图，直接完全理解为止，这段话称得上是ON-LSTM的设计总纲。）

3.2 设计：分段软化

现在要解决的问题就是，这两个层级怎么预测，即 $F_1$ , $F_2$ 怎么构建。用一个模型来输出一个整数不难，但是这样的模型通常都是不可导的，无法很好地整合到整个模型进行反向传播，所以，更好的方案是进行“软化”，即寻求一些光滑近似。

在这里插入图片描述

举个例子: $1_{d_{f}}$ = [0, 0, 0, 1, 0], $1_{d_{i}}$ = [0, 0, 0, 0, 1]. 则根据(6)式, 有 $\tilde{f_{t}}$ = [0, 0, 0, 1, 1], $\tilde{i_{t}}$ = [1, 1, 1, 1, 1], 所以 $w_{t} = \tilde{f_{t}} ∘ \tilde{i_{t}}$ = [0, 0, 0, 1, 1]. 即对这种情况(公式(4), $d_f$ <= $d_i$ , 表示信息有融合), 对4, 5位置处的信息进行融合, 1, 2, 3位置处变为 $\hat{c_{t}}$ .

在这里插入图片描述

注:

1、论文中将 $\overrightarrow{cs}(softmax(x))$ 简记为cumax(x)，这只是记号上的转换而已；
2、作为数列来看， $\tilde{f_{t}}$ 是一个单调递增的数列，而 $\tilde{i_{t}}$ 是一个单调递减的数列；
3、 $1_{d_{f}}$ 和 $1_{d_{i}}$ 的dimension是 (N, unit), 其中N为Batch size, unit是本层的单元数. 同样的, 隐藏状态hidden state $h_t$ 和细胞状态 $c_t$ 的dimension也都是 (N, unit). 而输入 $x_t$ 的dimension是 (N, input_dim).
4、由于3和1, 需要通过2个全连接层来估计参数, 这会加大计算量, 尤其是当unit和input_dim都被设置的很大的时候. 后面可能会有更好的低复杂度解决方案.

4. 试验

下面简单汇总一下ON-LSTM的实验，其中包括原作者的实现（PyTorch）以及苏剑林大神自己的复现（Keras）

原作者实现：https://github.com/yikangshen/Ordered-Neurons

苏神实现：https://github.com/bojone/on-lstm

4.1 分组层级

在这里插入图片描述
Notice: 这里减少的是下式中的(全连接层, 激活函数为softmax)的输出的单元个数, 因此减少了一定的计算量.

4.2 语言模型

在这里插入图片描述

4.3 无监督语法

如果仅仅是在常规的一些语言任务中超过普通LSTM，那么ON-LSTM也算不上什么突破，但ON-LSTM的一个令人兴奋的特性是它能够无监督地从训练好的模型（比如语言模型）中提取输入序列的层级树结构。提取的思路如下：

首先我们考虑：
在这里插入图片描述
它是 $\tilde{f_{t}}$ 在 $\overrightarrow{cs}$ 之前的结果，根据我们前面的推导，它就是历史信息的层级 $d_{f}$ 的一个软化版本，那么我们可以写出：

算法的大概意思是从最高层级处断开（这意味着当此处包含的历史信息最少，与前面所有内容的联系最为薄弱，最有可能是一个新的子结构的开始），然后递归处理，从而逐渐得到输入序列隐含的嵌套结构。作者是用三层的ON-LSTM训练了一个语言模型，然后用中间那层ON-LSTM的 $\tilde{f_{t}}$ 来计算层级，然后跟标注的语法结构对比，发现准确率颇高。我自己也在中文语料下尝试了一下：https://github.com/bojone/on-lstm/blob/master/lm_model.py

至于效果，因为我没做过也不了解语法分析，我也不知道怎么评价，反正好像看着是那么一回事，但是又好像不大对一样，所以各位读者自己评价好了～近一两年，无监督语法分析其实还有不少研究工作，可能要都读一读才能更深刻地理解ON-LSTM。

输入：苹果的颜色是什么
输出：
[
[
[
‘苹果’,
‘的’
],
[
‘颜色’,
‘是’
]
],
‘什么’
]

5. 思考&发散

文章最后，我们来一起思考几个问题。

RNN还有研究价值？

首先，有读者可能会困惑，都9102年了，居然还有人研究RNN类模型，还有研究价值吗？近年来，BERT、GPT等基于Attention和语言模型的预训练模型，在NLP的诸多任务上都提升了效果，甚至有文章直接说“RNN已死”之类的。事实上真的如此吗？我认为，RNN活得好好的，并且在将来的相当长时间内都不会死，原因至少包含下面几个：

第一，BERT之类的模型，以增加好几个数量级的算力为代价，在一些任务上提升了也就一两个百分点的效果，这样的性价比只有在学术研究和比赛刷榜才有价值，在工程上几乎没什么用（至少没法直接用）；
第二，RNN类的模型本身具有一些无可比拟的优势，比如它能轻松模拟一个计数函数，在很多序列分析的场景，RNN效果好得很；第三，几乎所有seq2seq模型（哪怕是BERT中）decoder都是一种RNN，因为它们基本都是递归解码的，RNN哪会消失？

单向ON-LSTM就够了？

然后，读者可能会有疑惑：你要析出层级结构，但是只用了单向的ON-LSTM，这意味着当前的层级分析还不依赖于将来的输入，这显然是不大符合事实的。这个笔者也有同样的困惑，但是作者的实验表明这样做效果已经够好了，可能自然语言的整体结构都倾向于是局部的、单向的（从左往右），所以对于自然语言来说单向也就够了。

如果一般情况下是否用双向比较好呢？双向的话是不是要像BERT那样用masked language model的方式来训练呢？双向的话又怎么计算层级序列呢？这一切都还没有完整的答案。至于无监督析出的结构是不是一定就符合人类自身理解的层级结构呢？这个也说不准，因为比较没有什么监督指引，神经网络就“按照自己的方式去理解”了，而幸运的是，神经网络的“自己的方式”，似乎跟人类自身的方式有不少重叠之处。

为什么析出层级考虑的是 $d_f$ 而不是 $d_i$ ？

读者可能会困惑，明明有两个master gate，为什么析出层级用 $d_f$ 而不是 $d_i$ ？要回答这个问题，我们要理解 $d_f$ 的含义。我们说 $d_f$ 是历史信息的层级，换言之，它告诉我们做出当前决策还要用多少历史信息。如果 $d_f$ 很大，意味着当前决策几乎用不着历史信息了，这意味着从当前开始就是一个新层级的开始，与历史输入几乎割断了联系。也就是从这种割断和联系中析出了层级结构，所以只能用 $d_f$ 。

能否用到CNN或者Attention？

最后，可能想到的一个困惑是，这种设计能不能用到CNN、Attention之中呢？换句话说能不能将CNN、Attention的神经元也排个序，融入层级结构信息呢？个人感觉是有可能的，但需要重新设计，因为层级结构被假设为连续嵌套的，RNN的递归性正好可以描述了这种连续性，而CNN、Attention的非递归性导致我们很难直接去表达这种连续嵌套结构。

不管怎样，我觉得这是个值得思考的主题，有进一步的思考结果我会和大家分享，当然也欢迎读者们和我分享你的思考。