（算法-差分）二维差分矩阵(普遍Scanner会超时，所以使用BufferedReader)

最新推荐文章于 2023-07-28 20:10:12 发布

原创最新推荐文章于 2023-07-28 20:10:12 发布 · 337 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #java

该博客讨论了一种二维差分矩阵的方法来高效处理矩阵操作，特别是在处理大量子矩阵加法操作时避免超时。通过建立差分矩阵并进行特定的更新，可以快速计算出最终矩阵。示例展示了如何使用BufferedReader代替Scanner以提高读取效率，并给出了完整的Java代码实现。

（算法-差分）二维差分矩阵（普遍Scanner会超时，所以使用BufferedReader）

题目描述
题目分析
解决方案

题目描述

输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数 n,m,q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含 5 个整数 x1,y1,x2,y2,c，表示一个操作。

输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例：

输出样例：

2 3 4 1
4 3 4 1
2 2 2 2

题目分析

思路和一维差分一样，只是改一下公式
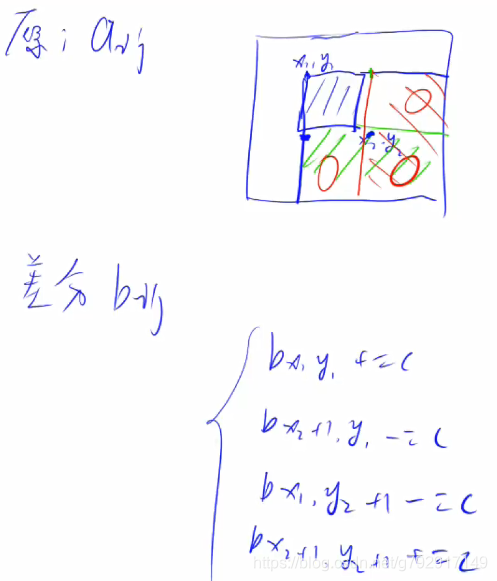
在这里插入图片描述
a[x1,y1]与a[x2,y2]之间的矩阵中的每一个数都加上c
先求a的差分矩阵b,

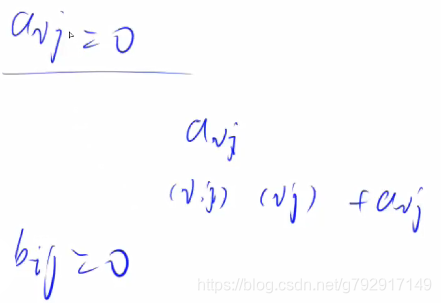
假定a[i,j] b[i,j]都等于0，a[i,j]就是在b数组的（i,j）(i,j) 位置插入a[i,j]

解决方案


import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.Scanner;

public class Main {
	static int N = 1010, n, m, q;
	static int[][] a = new int[N][N];
	static int[][] b = new int[N][N];

	static void insert(int x1, int y1, int x2, int y2, int c) {
		b[x1][y1] += c;
		b[x2 + 1][y1] -= c;
		b[x1][y2 + 1] -= c;
		b[x2 + 1][y2 + 1] += c;
	}

	public static void main(String[] args) throws IOException {
		// 普遍Scanner会超时，所以使用BufferedReader
		BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
		String[] str1 = reader.readLine().split(" ");

		n = Integer.parseInt(str1[0]);
		m = Integer.parseInt(str1[1]);
		q = Integer.parseInt(str1[2]);

		for (int i = 1; i <= n; i++) {
			 String[] str2 = reader.readLine().split(" ");
			for (int j = 1; j <= m; j++) {
				// 循环注入
				a[i][j] = Integer.parseInt(str2[j-1]);
				insert(i, j, i, j, a[i][j]);
			}
		}
		
		while (--q >= 0) {
			int x1, y1, x2, y2, c;
			String str3[] = reader.readLine().split(" ");
			x1 = Integer.parseInt(str3[0]);
			y1 = Integer.parseInt(str3[1]);
			x2 = Integer.parseInt(str3[2]);
			y2 = Integer.parseInt(str3[3]);
			c = Integer.parseInt(str3[4]);
			insert(x1, y1, x2, y2, c);
		}
		
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <=m; j++) {
				b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
				writer.write(b[i][j]+" ");
			}
			writer.write("\n");
		}
		//所有write下的内容，会先存在writers中，当启用flush以后，会输出存在其中的内容。如果没有调用flush，则不会将writer中的内容进行输出。
        writer.flush();
        reader.close();
        writer.close();
	}
}