一、假设检验
根据样本(小流量)的观测结果,拒绝或接受关于总体(全部流量)的某个假设,称为假设检验。
假设检验的基本依据是小概率事件原理(小概率事件几乎不发生),如果小概率事件发生了,则有充分理由推翻原假设,否则接受原假设,检验的具体过程是:
-
首先假定原假设成立,并寻找一个原假设成立条件下的发生概率微小的事件,称为检验事件,对应的统计量称为检验统计量
-
其次是采集样本
-
最后观测步骤 1 所定义的小概率事件是否发生
-
- 若小概率事件发生,则拒绝原假设,接受备用假设
- 若小搞错了时间未发生,则接受原假设,拒绝备用假设
具体到AB实验中,涉及实验组和对照组组两个总体,假设实验的某个目标指标满足正态分布,实验组和对照组分别记为 X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 ) X\sim \mathcal{N}(\mu_1, \sigma_1^2), Y \sim \mathcal{N}(\mu_2, \sigma_2^2) X∼N(μ1,σ12),Y∼N(μ2,σ22),常见检验问题是判断实验组对比对照组是否有效,具体又分为几类情况:
I. 原假设 H 0 : μ 1 ≤ μ 2 H_0: \mu_1\le \mu_2 H0:μ1≤μ2实验组对比对照组负向或无效;备用假设 H 1 : μ 1 > μ 2 H_1:\mu_1 > \mu_2 H1:μ1>μ2,实验组对比对照组正向
II. 原假设 H 0 : μ 1 ≥ μ 2 H_0:\mu_1\ge \mu_2 H0:μ1≥μ2实验对比对照组正向或无效;备用假设 H 1 : μ 1 < μ 2 H_1:\mu_1 < \mu_2 H1:μ1<μ2,实验组对比对照组负向
III. 原假设 H 0 : μ 1 = μ 2 H_0:\mu_1= \mu_2 H0:μ1=μ2实验对比对照组无效;备用假设 H 1 : μ 1 ≠ μ 2 H_1:\mu_1 \ne \mu_2 H1:μ1=μ2,实验有效,但未区分正向还是负向效果
与之等价的三个假设检验问题是:
I. 原假设 H 0 : μ 1 − μ 2 ≤ 0 H_0:\mu_1 - \mu_2 \le 0 H0:μ1−μ2≤0;备用假设 H 1 : μ 1 − μ 2 > 0 H_1:\mu_1 - \mu_2 > 0 H1:μ1−μ2>0
II. 原假设 H 0 : μ 1 − μ 2 ≥ 0 H_0:\mu_1- \mu_2\ge 0 H0:μ1−μ2≥0;备用假设 H 1 : μ 1 − μ 2 < 0 H_1:\mu_1 - \mu_2< 0 H1:μ1−μ2<0
III. 原假设 H 0 : μ 1 − μ 2 = 0 H_0:\mu_1- \mu_2 = 0 H0:μ1−μ2=0;备用假设 H 1 : μ 1 − μ 2 ≠ 0 H_1:\mu_1 - \mu_2 \ne 0 H1:μ1−μ2=0
如何寻找一个事件,满足在原假设成立条件下发生的概率微小 ?发生概率多小能满足要求 ?
第二个问题比较好回答,一般取 0.01 或 0.05,记为 α = 0.01 ∣ 0.05 \alpha = 0.01|0.05 α=0.01∣0.05,称为检验的显著性。第一个问题需要费一番推导。
以假设检验问题 I 为例,实验收集的样本记为 { X 1 , X 2 . . . , X n } , { Y 1 , Y 2 , . . . , Y 3 } \{X_1, X_2...,X_n\}, \{Y_1, Y_2, ..., Y_3\} {X1,X2...,Xn},{Y1,Y2,...,Y3}, 样本均值 X ‾ = ∑ i X i n , Y ‾ = ∑ i Y I m \overline{X} = \frac{\sum_i X_i}{n},\overline{Y} = \frac{\sum_iY_I}{m} X=n∑iXi,Y=m∑iYI分别总体均值 μ 1 , μ 2 \mu_1, \mu_2 μ1,μ2的无偏相合估计,样本均值之差 X ‾ − Y ‾ \overline{X}-\overline{Y} X−Y是总体均值差 μ 1 − μ 2 \mu_1-\mu_2 μ1−μ2的无偏相合估计,因此样本均值之差 X ‾ − Y ‾ \overline{X}-\overline{Y} X−Y大概率是分布在 μ 1 − μ 2 \mu_1-\mu_2 μ1−μ2附近,直观思考,原假设成立的条件下, X ‾ − Y ‾ \overline{X}-\overline{Y} X−Y大概率落在非正数附近, X ‾ − Y ‾ \overline{X}-\overline{Y} X−Y取值为较大的正数的概率较小,如下图:
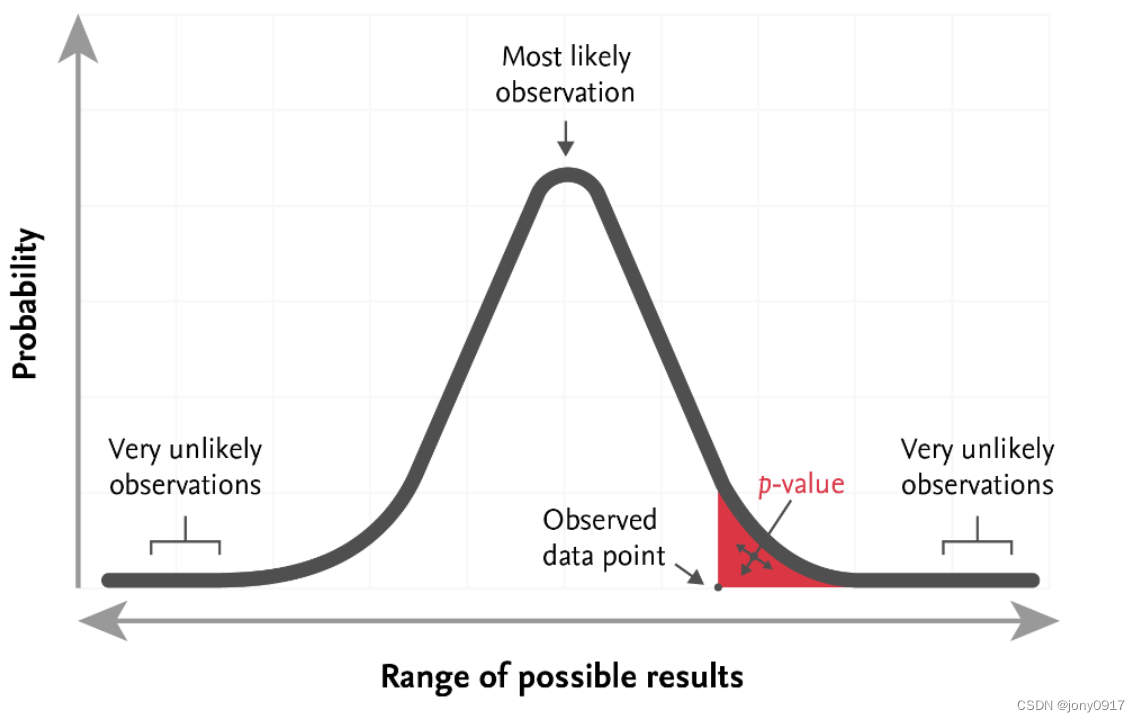
因此假设检验问题 I 原假设成立条件下的小概率事件定义为:$ {\overline{X}-\overline{Y} > c}$
下面需要做的是在给定小概率值 α \alpha α(也就是检验的显著性)的条件下确定阈值 c ,也就是满足不等式 P ( X ‾ − Y ‾ > c ) ≤ α P(\overline{X}-\overline{Y} > c) \le \alpha P(X−Y>c)≤α的实数 c.
由中心极限定理得到:
X ‾ ∼ N ( μ 1 , σ 1 2 / n ) Y ‾ ∼ N ( μ 2 , σ 2 2 / m ) \overline{X} \sim \mathcal{N}(\mu_1, \sigma_1^2/n)\\ \overline{Y} \sim \mathcal{N}(\mu_2, \sigma_2^2/m) X∼N(μ1,σ12/n)Y∼N(μ2,σ22/m)
为了确定阈值 c,需要分几种情况:
- 总体方差 σ 1 2 , σ 2 2 \sigma_1^2, \sigma_2^2 σ12,σ22已知
- 总体方差 σ 1 2 = σ 2 2 = σ 2 \sigma_1^2 = \sigma_2^2 = \sigma^2 σ12=σ22=σ2,且未知
- 总体方差 σ 1 2 ≠ σ 2 2 \sigma_1^2\ne\sigma_2^2 σ12=σ22,且未知
- 总体方差 σ 1 2 ≠ σ 2 2 \sigma_1^2\ne \sigma_2^2 σ12=σ22,且未知,大样本场景
首先考虑最简单的情况1, 由独立正态分布特性得到:
X ‾ − Y ‾ ∼ N ( μ 1 − μ 2 , σ 1 2 n + σ 2 2 m ) \overline{X}-\overline{Y} \sim \mathcal{N}(\mu_1 - \mu_2, \frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m} ) X−Y∼N(μ1−μ2,nσ12+mσ22)
( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) σ 1 2 n + σ 2 2 m ∼ N ( 0 , 1 ) \frac{(\overline{X}-\overline{Y}) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} \sim \mathcal{N}(0, 1) nσ12+mσ22(X−Y)−(μ1−μ2)∼N(0,1): 正态分布性质
P ( ( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) σ 1 2 n + σ 2 2 m > z α ) = α P(\frac{(\overline{X}-\overline{Y}) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} > z_{\alpha}) =\alpha P(nσ12+mσ22(X−Y)−(μ1−μ2)>zα)=α : 由正态分布的上分位z_{\alpha}数定义
P H 0 ( X ‾ − Y ‾ σ 1 2 n + σ 2 2 m − μ 1 − μ 2 σ 1 2 n + σ 2 2 m > z α ) = α P_{H_0}(\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} - \frac{\mu_1-\mu_2}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} >z_{\alpha}) = \alpha PH0(nσ12+mσ22X−Y−nσ12+mσ22μ1−μ2>zα)=α
P H 0 ( X ‾ − Y ‾ σ 1 2 n + σ 2 2 m > z α + μ 1 − μ 2 σ 1 2 n + σ 2 2 m ) = α P_{H_0}(\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} >z_{\alpha} + \frac{\mu_1-\mu_2}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}}) = \alpha PH0(nσ12+mσ22X−Y>zα+nσ12+mσ22μ1−μ2)=α
P H 0 ( X ‾ − Y ‾ σ 1 2 n + σ 2 2 m > z α ) ≤ P H 0 ( X ‾ − Y ‾ σ 1 2 n + σ 2 2 m > z α + μ 1 − μ 2 σ 1 2 n + σ 2 2 m ) = α P_{H_0}(\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} >z_{\alpha}) \le P_{H_0}(\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} >z_{\alpha} + \frac{\mu_1-\mu_2}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}}) = \alpha PH0(nσ12+mσ22X−Y>zα)≤PH0(nσ12+mσ22X−Y>zα+nσ12+mσ22μ1−μ2)=α: 由事件和子事件概率关系
P H 0 ( X ‾ − Y ‾ > z α ∗ σ 1 2 n + σ 2 2 m ) ≤ α P_{H_0}(\overline{X}-\overline{Y} >z_{\alpha} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}) \le \alpha PH0(X−Y>zα∗nσ12+mσ22)≤α
c = z α ∗ σ 1 2 n + σ 2 2 m c = z_{\alpha} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}} c=zα∗nσ12+mσ22
概念整理:
-
检验显著性: α \alpha α
-
检验统计量:$Z= \overline{X}-\overline{Y} $
-
拒绝域: W I = { Z > z α ∗ σ 1 2 n + σ 2 2 m } W_I = \{ Z >z_{\alpha} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}\} WI={Z>zα∗nσ12+mσ22}
因为 { X ‾ − Y ‾ > z α ∗ σ 1 2 n + σ 2 2 m } \{\overline{X} - \overline{Y} > z_{\alpha} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}\} {X−Y>zα∗nσ12+mσ22}与 { X ‾ − Y ‾ σ 1 2 n + σ 2 2 m > z α } \{ \frac{\overline{X} - \overline{Y}}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} >z_{\alpha} \} {nσ12+mσ22X−Y>zα}是等价事件,因此检验问题 1 经常采用的
- 检验统计量是 u = X ‾ − Y ‾ σ 1 2 n + σ 2 2 m u = \frac{\overline{X} - \overline{Y}}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} u=nσ12+mσ22X−Y
- 拒绝域为 W I = { u > z α } W_I = \{u > z_{\alpha}\} WI={u>zα}
p-value:
以检验问题 I 为例
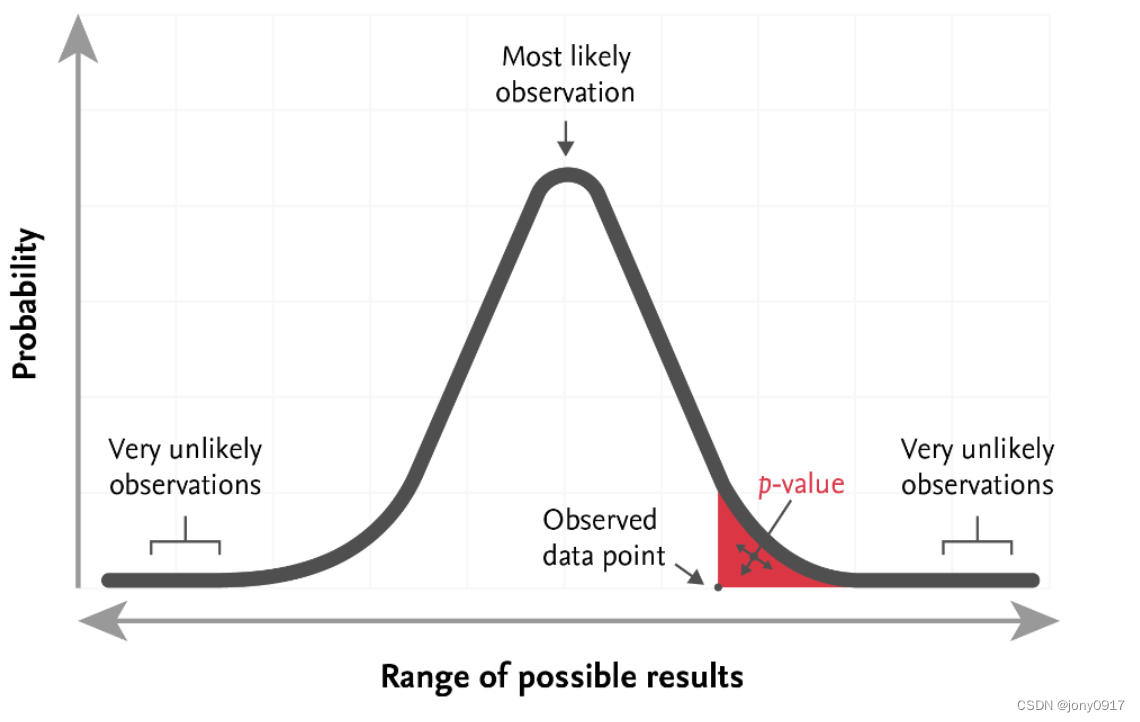
在一个假设检验问题中,拒绝原假设的最小显著性水平成为 p 值。
X ‾ − Y ‾ ∼ N ( μ 1 − μ 2 , σ 1 2 n + σ 2 2 m ) \overline{X}-\overline{Y} \sim \mathcal{N}(\mu_1 - \mu_2, \frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m} ) X−Y∼N(μ1−μ2,nσ12+mσ22)
p = P ( T > X ‾ − T ‾ ) p= P(T > \overline{X} - \overline{T}) p=P(T>X−T)
利用p值和给定的显著性水平 α \alpha α:
- 若 α ≥ p \alpha \ge p α≥p,则拒绝原假设
- 若 α < p \alpha < p α<p,则接受原假设
p 值越小,拒绝原假设的理由越充分。
检验错误:
原假设实际成立但被拒绝的错误,称为 I 类错误,对应AB实验中推全了一个没有效果的实验,错误发生的概率记为 α \alpha α
原假设实际不成立但被接受的错误,称为 II 类错误,对应AB实验中一个有效果的实验没被推全,错误发生概率记为 β \beta β.
以上的检验过程保证原假设成立但被推翻的概率小于\alpha.
样本量一定的情况下,无法同事降低I类错误和II类错误的概率,一般通过保证 I 类错误不高于一个阈值的情况下,通过增大样本量,控制II错误概率。
最小样本量:
以检验问题 I 为例,考察接受原假设的概率:
P ( X ‾ − Y ‾ σ 1 2 n + σ 2 2 m < z α ) = P ( ( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) σ 1 2 n + σ 2 2 m < z α − μ 1 − μ 2 σ 1 2 n + σ 2 2 m ) P(\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} < z_{\alpha}) = P(\frac{(\overline{X}-\overline{Y}) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} < z_{\alpha} - \frac{\mu_1-\mu_2}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} ) P(nσ12+mσ22X−Y<zα)=P(nσ12+mσ22(X−Y)−(μ1−μ2)<zα−nσ12+mσ22μ1−μ2)
( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) σ 1 2 n + σ 2 2 m ∼ N ( 0 , 1 ) \frac{(\overline{X}-\overline{Y}) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} \sim \mathcal{N}(0, 1) nσ12+mσ22(X−Y)−(μ1−μ2)∼N(0,1)
P ( ( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) σ 1 2 n + σ 2 2 m < z α − μ 1 − μ 2 σ 1 2 n + σ 2 2 m ) = Φ ( z α − μ 1 − μ 2 σ 1 2 n + σ 2 2 m ) < β P(\frac{(\overline{X}-\overline{Y}) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} < z_{\alpha} - \frac{\mu_1-\mu_2}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}}) = \Phi(z_{\alpha} - \frac{\mu_1-\mu_2}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}}) < \beta P(nσ12+mσ22(X−Y)−(μ1−μ2)<zα−nσ12+mσ22μ1−μ2)=Φ(zα−nσ12+mσ22μ1−μ2)<β
z α − μ 1 − μ 2 σ 1 2 n + σ 2 2 m < z 1 − β z_{\alpha} - \frac{\mu_1-\mu_2}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} < z_{1 - \beta} zα−nσ12+mσ22μ1−μ2<z1−β
假设 m = n
n > ( z α + z β ) σ 1 2 + σ 2 2 μ 1 − μ 2 ( 1 ) \sqrt{n} > \frac{(z_\alpha + z_\beta)\sqrt{\sigma_1^2 + \sigma^2_2}}{\mu_1 - \mu_2} \space\space\space\space\space\space(1) n>μ1−μ2(zα+zβ)σ12+σ22 (1)
启发:
-
指标总体的方差越大,需要的最小样本量越大
-
控制错误概率越低,需要的最小样本量越大,一般 α = 0.01 、 0.05 , β = 0.2 \alpha = 0.01、0.05, \beta = 0.2 α=0.01、0.05,β=0.2
-
实验组相对对照组提升 μ 1 − μ 2 \mu_1 - \mu_2 μ1−μ2越大,需要的样本量越小;提升越小,需要的最小样本量越大
-
- 当 μ 1 \mu_1 μ1从左侧无限接近 μ 2 \mu_2 μ2,所需要的最小样本量接近无限大
-
实验最短观测周期:T = ( z α + z β ) σ 1 2 + σ 2 2 μ 1 − μ 2 \frac{(z_\alpha + z_\beta)\sqrt{\sigma_1^2 + \sigma^2_2}}{\mu_1 - \mu_2} μ1−μ2(zα+zβ)σ12+σ22 / 单位时长累积样本数量
第2种情况,样本方差未知但相等:
s x 2 = 1 n − 1 ∑ ( x i − x ‾ ) 2 s y 2 = 1 m − 1 ∑ ( y i − y ‾ ) 2 s w 2 = ( n − 1 ) s x 2 + ( m − 1 ) s y 2 n + m − 2 s_x^2 = \frac{1}{n-1}\sum (x_i - \overline{x})^2 \\ s_y^2 = \frac{1}{m-1}\sum(y_i - \overline{y})^2 \\ s_w^2 = \frac{(n-1)s_x^2 + (m-1)s_y^2}{n+m-2} sx2=n−11∑(xi−x)2sy2=m−11∑(yi−y)2sw2=n+m−2(n−1)sx2+(m−1)sy2
( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) s w 1 n + 1 m ∼ t ( n + m − 2 ) \frac{(\overline{X} - \overline{Y}) - (\mu_1 - \mu_2)}{s_w\sqrt{\frac{1}{n} + \frac{1}{m}}} \sim t(n + m - 2) swn1+m1(X−Y)−(μ1−μ2)∼t(n+m−2)
-
检验统计量: t = X ‾ − Y ‾ s w 1 n + 1 m t = \frac{\overline{X} - \overline{Y}}{s_w\sqrt{\frac{1}{n} + \frac{1}{m}}} t=swn1+m1X−Y
-
拒绝域: W I = { t > t 1 − α ( n + m − 2 ) } W_I = \{ t > t_{1-\alpha}(n + m- 2) \} WI={t>t1−α(n+m−2)}
第3中情况,样本样本方差未知,但不等
-
检验统计量: t = X ‾ − Y ‾ s x 2 n + s y 2 m t = \frac{\overline{X} - \overline{Y}}{\sqrt{\frac{s^2_x}{n} + \frac{s_y^2}{m}}} t=nsx2+msy2X−Y
-
拒绝域: W I = { t > t 1 − α ( l ) } l = ( s x 2 n + s y 2 m ) 2 / [ s x 4 n 2 ( n − 1 ) + s y 4 m 2 ( m − 1 ) ] W_I = \{ t > t_{1-\alpha}(l) \} \\ l = (\frac{s_x^2}{n} + \frac{s_y^2}{m})^2/[\frac{s_x^4}{n^2(n-1)} +\frac{s_y^4}{m^2(m-1)} ] WI={t>t1−α(l)}l=(nsx2+msy2)2/[n2(n−1)sx4+m2(m−1)sy4]
第4种情况,大样本情况
- 检验统计量: u = X ‾ − Y ‾ s x 2 n + s y 2 m u = \frac{\overline{X} - \overline{Y}}{\sqrt{\frac{s^2_x}{n} + \frac{s_y^2}{m}}} u=nsx2+msy2X−Y
- 拒绝域: W I = { u > z α } W_I = \{u > z_{\alpha}\} WI={u>zα}
二、区间估计
点估计不能提供估计参数的估计误差大小,所以点估计主要用在定性分析的场景,或在对总体参数要求不精确时使用,而在需要用精确总体参数的数据进行决策时则很少使用,这种场景主要使用区间估计。
第1种情况,总体方差已知:
( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) σ 1 2 n + σ 2 2 m ∼ N ( 0 , 1 ) \frac{(\overline{X}-\overline{Y}) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} \sim \mathcal{N}(0, 1) nσ12+mσ22(X−Y)−(μ1−μ2)∼N(0,1)
P ( − z α / 2 ≤ ( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) σ 1 2 n + σ 2 2 m ≤ z α / 2 ) = 1 − α P(-z_{\alpha/2}\le\frac{(\overline{X}-\overline{Y}) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} \le z_{\alpha/2}) = 1- \alpha P(−zα/2≤nσ12+mσ22(X−Y)−(μ1−μ2)≤zα/2)=1−α
P ( X ‾ − Y ‾ − z α / 2 ∗ σ 1 2 n + σ 2 2 m ≤ μ 1 − μ 2 ≤ X ‾ − Y ‾ + z α / 2 ∗ σ 1 2 n + σ 2 2 m ) = 1 − α P(\overline{X}-\overline{Y} - z_{\alpha/2} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}\le \mu_1-\mu_2\le \overline{X}-\overline{Y} + z_{\alpha/2} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}) = 1 - \alpha P(X−Y−zα/2∗nσ12+mσ22≤μ1−μ2≤X−Y+zα/2∗nσ12+mσ22)=1−α
- μ 1 − μ 2 \mu_1 - \mu_2 μ1−μ2的 1 − α 1 -\alpha 1−α置信区间 [ X ‾ − Y ‾ − z α / 2 ∗ σ 1 2 n + σ 2 2 m , X ‾ − Y ‾ + z α / 2 ∗ σ 1 2 n + σ 2 2 m ] [\overline{X}-\overline{Y} - z_{\alpha/2} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}, \overline{X}-\overline{Y} + z_{\alpha/2} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}] [X−Y−zα/2∗nσ12+mσ22,X−Y+zα/2∗nσ12+mσ22]
第2种情况,总体方差未知但相等:
- μ 1 − μ 2 \mu_1 - \mu_2 μ1−μ2的 1 − α 1 -\alpha 1−α置信区间 [ X ‾ − Y ‾ − t 1 − α / 2 ( n + m − 2 ) ∗ s w ∗ 1 n + 1 m , X ‾ − Y ‾ + t 1 − α / 2 ( n + m − 2 ) ∗ s w ∗ 1 n + 1 m ] [\overline{X}-\overline{Y} - t_{1-\alpha/2}(n+m-2)*s_w * \sqrt{\frac{1}{n} + \frac{1}{m}}, \overline{X}-\overline{Y} + t_{1-\alpha/2}(n+m-2) *s_w* \sqrt{\frac{1}{n} + \frac{1}{m}}] [X−Y−t1−α/2(n+m−2)∗sw∗n1+m1,X−Y+t1−α/2(n+m−2)∗sw∗n1+m1]
第3种情况:
- μ 1 − μ 2 \mu_1 - \mu_2 μ1−μ2的 1 − α 1 -\alpha 1−α置信区间 [ X ‾ − Y ‾ − t 1 − α / 2 ( 1 ) ∗ s x 2 n + s y 2 m , X ‾ − Y ‾ + t 1 − α / 2 ( l ) ∗ s x 2 n + s y 2 m ] [\overline{X}-\overline{Y} - t_{1-\alpha/2}(1) * \sqrt{\frac{s_x^2}{n} + \frac{s_y^2}{m}}, \overline{X}-\overline{Y} + t_{1-\alpha/2}(l) * \sqrt{\frac{s_x^2}{n} + \frac{s_y^2}{m}}] [X−Y−t1−α/2(1)∗nsx2+msy2,X−Y+t1−α/2(l)∗nsx2+msy2]
第4种情况:
- μ 1 − μ 2 \mu_1 - \mu_2 μ1−μ2的 1 − α 1 -\alpha 1−α置信区间 [ X ‾ − Y ‾ − u 1 − α / 2 ∗ s x 2 n + s y 2 m , X ‾ − Y ‾ + u 1 − α / 2 ∗ s x 2 n + s y 2 m ] [\overline{X}-\overline{Y} - u_{1-\alpha/2} * \sqrt{\frac{s_x^2}{n} + \frac{s_y^2}{m}}, \overline{X}-\overline{Y} + u_{1-\alpha/2} * \sqrt{\frac{s_x^2}{n} + \frac{s_y^2}{m}}] [X−Y−u1−α/2∗nsx2+msy2,X−Y+u1−α/2∗nsx2+msy2]
三、区间估计与假设检验的关系
- 若检验显著水平 α \alpha α 拒绝域为W,则对立事件 W ‾ \overline{W} W就是相应参数的 1 − α 1 - \alpha 1−α置信区间
- W ‾ \overline{W} W为相应参数 1 − α 1 - \alpha 1−α置信区间,则对立事件W为检验显著水平 α \alpha α的拒绝域
四、更多
两个二项分布指标的分析
。。。





















 894
894











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








