1.简介:
为了能看懂各种材料学上的专业术语,简单学一点合金材料学十分必要。我们主要研究的是金属材料,因此本文将着重介绍金属材料。本文材料基本来自于北京大学出版社出版的《材料科学概论》,这是一本不错的材料入门教材。
2.晶体(Crystal)
金属材料在固态下是晶体(Crystal)。晶体就是内部原子(Atom)或分子(Molecule)在三维空间中作有规则的周期性重复排列的物体。晶体中这种排列方式被称为晶体结构。晶体结构往往决定了金属(Metal)的性能。
2.1 原子间的键合(Interatomic Bonding)
键合就是原子间的连接方式,也是导致物质性能不一样的主要原因。我们在金属方面主要讨论的是结合力的不同,根据结合力的强弱,可以把结合力分为两种:
- 结合力较强的主键(Primary Bond):离子键、共价键和金属键。
- 结合力较弱的次价键(Secondary Bond):范德瓦尔斯键和氢键。
2.1.1 离子键(Ionic Bond)
金属元素中,有的容易失去电子比如IA 和IIA族的元素,还有的元素容易得到电子比如VIA和VII族。现在复习一下高中化学:原子失去电子(Electron)会变成阴离子(Anion),原子得到电子会变成阳离子(Cation),阴阳离子结合会形成一种稳定的状态,把它们结合在一起的就是离子键,靠离子键结合的原子以离子(Ion)的形式存在。最常见的例子是NaCl。离子键结合比较紧密,所以这一类物质的熔点很高,但是比较脆,因为相对位移可以破坏其结构,通俗点理解就是Na离子和其他Cl离子结合,所以食盐容易被碾碎。同时,因为电子无法自由移动,所以他们往往都是绝缘体。
2.1.2 共价键(Covalent Bond)
有很多元素的原子电子得失都困难,这个时候它们可以通过共用电子对(Shared Electron Pair)形成共价键来进行结合。比如金刚石就是C元素公用的电子对。共价键的结合力极大,所以共价晶体的结构往往比较稳定。
2.1.3 金属键(Metallic Bond)
金属元素极其容易失去电子,但是他们互相之间也能靠金属键形成稳定的结构。当金属元素在一起时,金属元素的原子核排列在一起形成晶格( Crystal Lattice),然后它们的全部电子都在晶格当中做无规则运动。
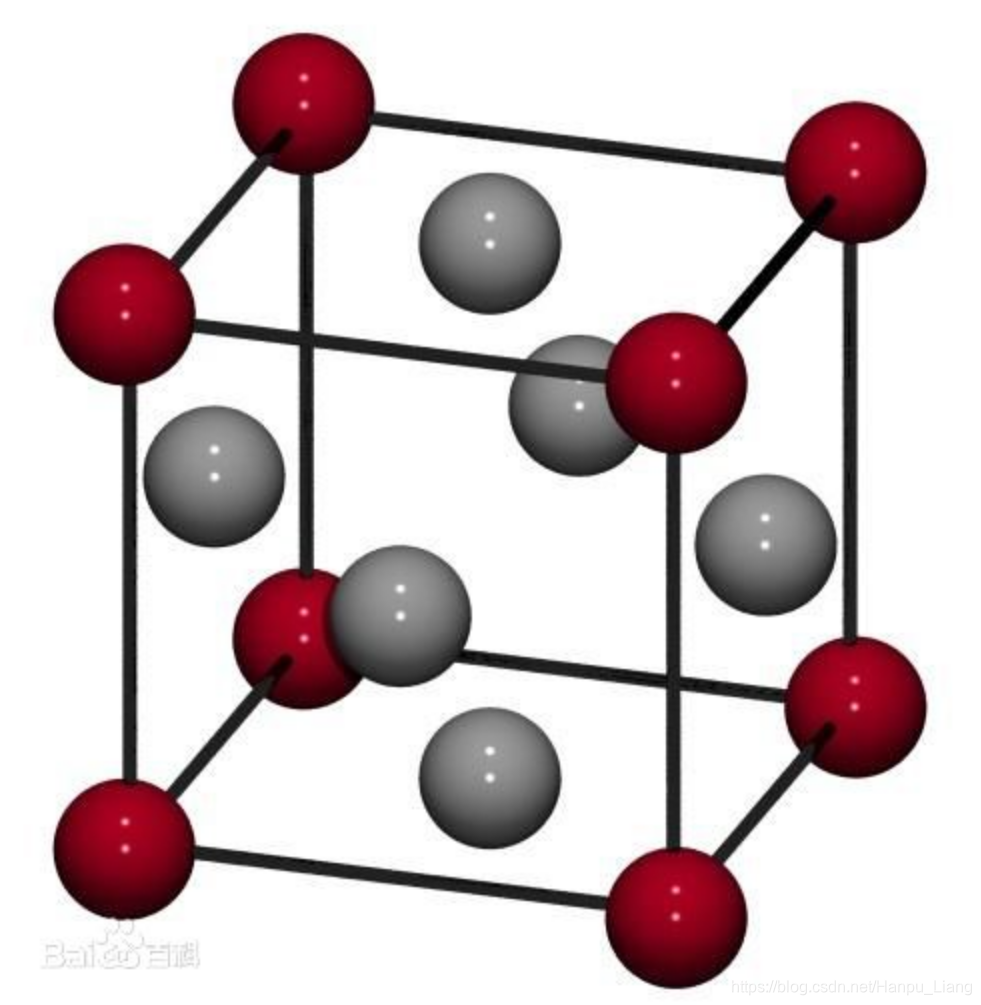
如图,红色是金属元素的原子核,灰色是电子,红色的原子核共同组成晶格。电子在晶格中形成电子云。电子和原子核互相作用产生的力就是金属键。金属键没有饱和性(Saturation),也就是说你现在有一块铁,你找另一块铁来把它们压在一起,也可以最终紧密结合。金属键的特点是压缩的越紧密,结构越稳定,所以古代铸剑要捶打。金属键导致了金属有很好的导电性(Electrical Conductivity),导热性(Thermal Conductivity)和延展性(Ductility)。说一点无关的内容(感觉有趣),电阻产生的原因:电子虽然在金属内部到处跑,但是不会跑出去,因为原子核对是正性的,对负性的电子有吸附作用,电流是很多电子的定向移动,但是在移动过程中会被原子核拉扯,故而形成电阻,而且金属的原子核其实也不是固定不动的,也在做无规则运动,所以当它运动方向和电流不一致的时候,电阻会增加,加热会导致金属的原子核运动加快,最后电阻加大,绝对零度,原子核不动,所以电阻可以看作0。金属在发生形变时仍然可以维持金属键,所以延展性好。同时金属容易吸收可见光的能量所以不透明,然后形成电子跃迁,最后电子回到低能级时候又把能量以电磁波的形式吐出来,形成金属光泽,不同的金属吸收的能量不一样,所以产生的金属光泽也不一样。
2.1.4 范德华力(Van der Waals Force)
范德华力又叫做范德瓦尔斯力,它可以看作磁力的一种。这是一种很小的外部力,远没有前面讨论的三种内部力作用强,很容易形变,形成的分子熔点低,硬度也不高。它其实是离子或者原子由于热振动或者电磁振动,导致电子全跑一边,然后一边就成阳极一边成阴极,然后原子或者离子就可以结合在一起,但是电子虽然跑一边,但是也不是全跑了,所以这种磁力很弱。
2.1.5 氢键(Hydrogen Bond)
它的力很强但是比化学键弱,是氢原子独有的。因为氢原子整体显阳性,那么遇到电负性强的原子就很容易被结合在一起。
2.1.6 小结
金属合金中的键其实有很多,不单单只有金属键,往往还有范德华力,以及少量的共价键等,共同形成一个稳定的结构。
2.2 晶体学基础
2.2.1 空间点阵(Space Lattice)
基本概念
由于原子电子分子都在不停的运动,所以不容易直接研究。我们可以把它们进行抽象,每一个点代表一个原子,分子,或者一群原子,点和点之间完全等价,然后再用平行线把它们连接,这样就可以表示这个晶体内部的一个抽象结构,我们将其称之为空间点阵。
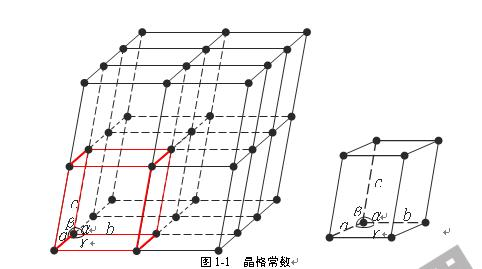
晶胞( Unit Cell)
我们可以从上面的图中看到空间点阵是由一个个的格子组成的,这些格子我们就称之为晶胞。晶胞的重复堆叠就可以组成一个晶体的点阵。当然,因为点阵本身就是一个抽象出来的东西,所以同一种晶体,它的点阵可以不同,即便点阵相同,晶胞也可以不同(你可以一次取出6个格子,也可以斜着取),所以我们取法要尽可能简单,一般取平行六面体八个角上都有点,当然你也可以不这样取,不管怎么取,首先要方便于研究。
晶胞的描述:我们在晶胞的几个点上任取一点(就像数学里面一样,往往取左下角的点,保证坐标系内的值都是正数),然后建立不一定是直角的坐标系x,y,zx,y,zx,y,z(称之为晶轴(Crystallographic Axes))。晶胞上面的点,我们称之为阵点(Lattice Point)。然后坐标系上面的三条棱的边长a,b,ca,b,ca,b,c和棱之间的夹角α,β,γ\alpha,\beta,\gammaα,β,γ 6个参数可以表示任意的晶胞形状,同时还可以表述点阵的形状(因为点阵也是晶胞的堆砌)。
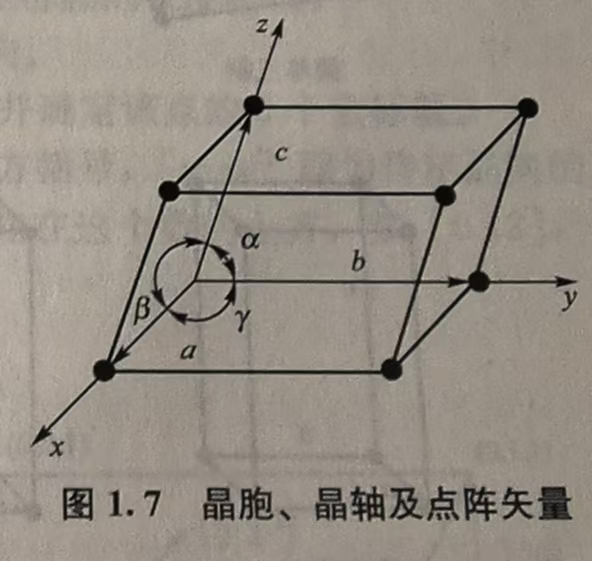
晶系(Crystal System)
根据上面的6个参数,所有的点阵可以分为7个晶系。如图:

布拉菲点阵(Bravais Lattice)
法国科学家布拉菲(Bravais)用数学证明了,在7个晶系下,点阵最多有14种,如图:
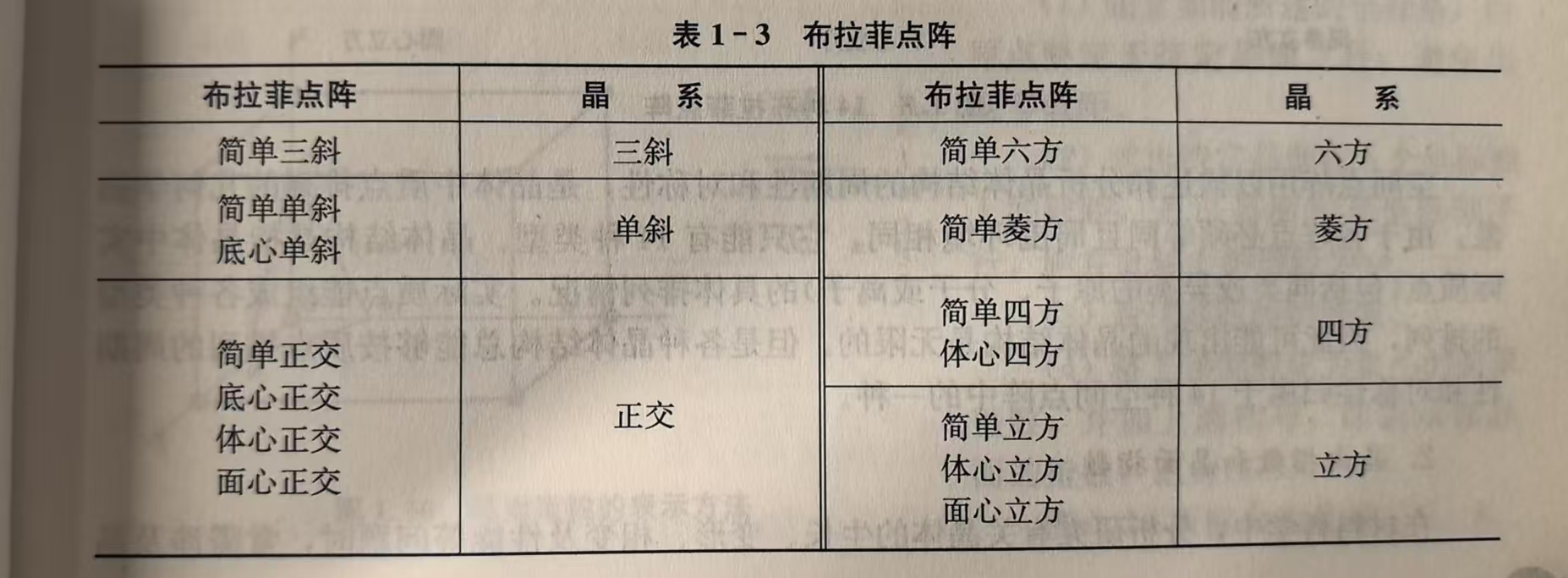
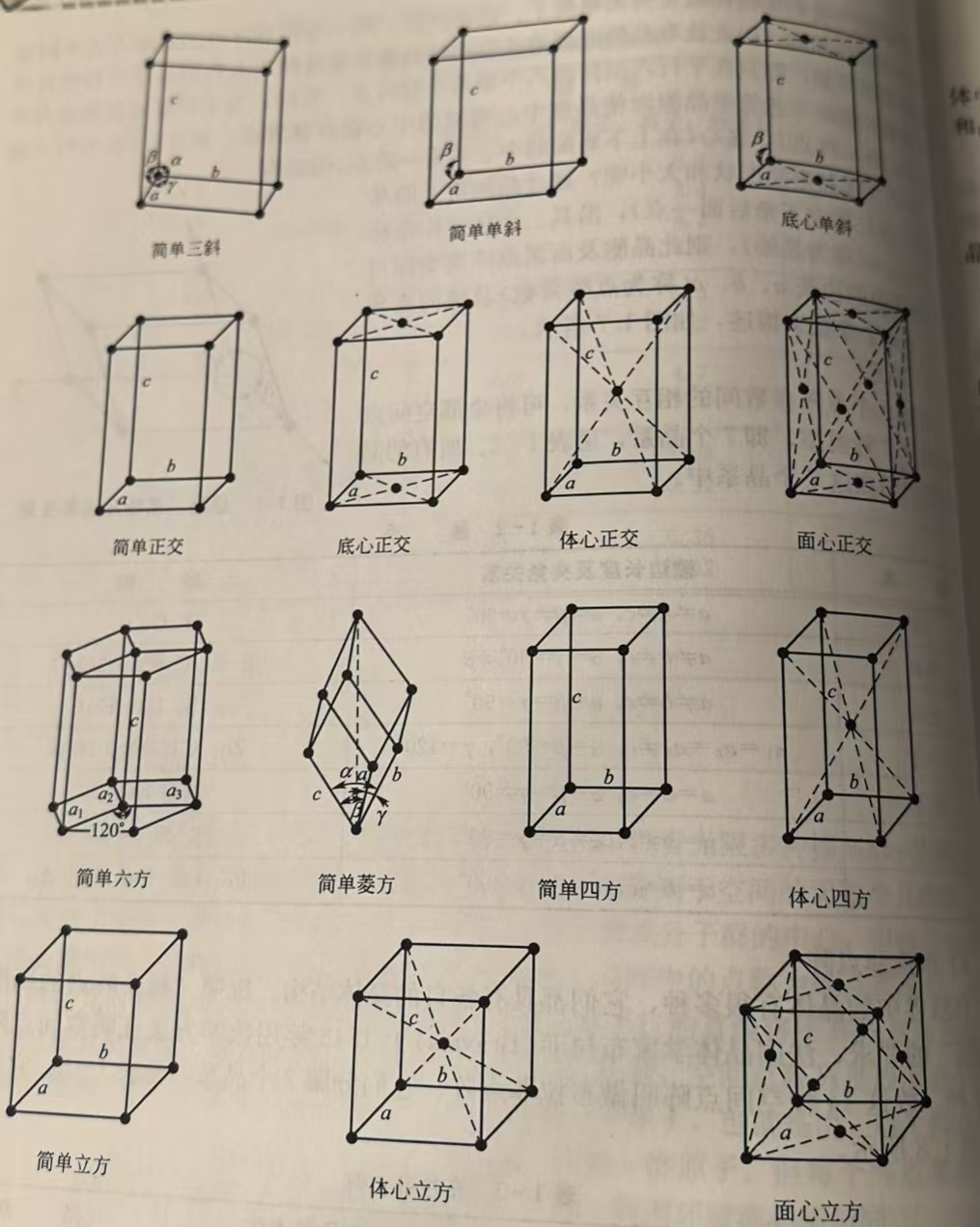
要注意的是,晶体的实际结构有无限种可能,但是我们总可以根据其周期性和对称性,把它归于这14种结构中的一种。现在分别看看:
1、立方晶系(Cubic System)
特征: a = b = c; α = β = γ = 90°
最高对称性, 常见金属如铝、铜、金、银属于此晶系。
2、六方晶系(Hexagonal System)
特征: a = b ≠ c; α = β = 90°, γ = 120°
常见材料: 镁、锌、钛等。
3、四方晶系(Tetragonal System)
特征: a = b ≠ c; α = β = γ = 90°
常见材料: 二氧化锡、白锡等。
4、三方晶系(Trigonal System)
特征: a = b = c; α = β = γ ≠ 90°
常见材料: 方解石、石英(α-SiO₂)。
5、正交晶系(Orthorhombic System)
特征: a ≠ b ≠ c; α = β = γ = 90°
常见材料: 硫、碘、橄榄石。
6、单斜晶系(Monoclinic System)
特征: a ≠ b ≠ c; α = γ = 90°, β ≠ 90°
常见材料: 石膏、单斜硫。
7、三斜晶系(Triclinic System)
特征: a ≠ b ≠ c; α ≠ β ≠ γ ≠ 90°
对称性最低, 常见材料: 石膏、单
2.2.2 晶向指数(Miller Indices for Directions)和晶面指数(Miller Indices for Planes)
晶体中某些面的朝向称之为晶向(Crystallographic Direction),这一面仅有原子构成称为晶面(Crystallographic Plane)。使用米勒(Miller)指数来描述晶向和晶面。
晶向指数(简称:Direction Indices)
晶向指数的确定有点复杂:
- 建立晶胞坐标系(上面说过)
- 过原点O作一条平行于我们要确定的晶向的平行线
- 在OP上找离O最近的一个阵点,并确定其x,y,zx,y,zx,y,z
- 把x,y,zx,y,zx,y,z如果不是整数全部通分然后取分子,然后获得uvwuvwuvw,我们称[uvw][uvw][uvw]为晶向指数。如果晶向指数中有负数,则在对应数字上面加一横,比如u是负数[uˉvw][\bar{u}vw][uˉvw]。
要注意,一个晶向是一个向量,在一个点阵中是无数平行线。如果几个晶向上的每隔一段等长的距离,穿过的阵点数量一致,则称它们属于同一晶向族(Family of Directions)。
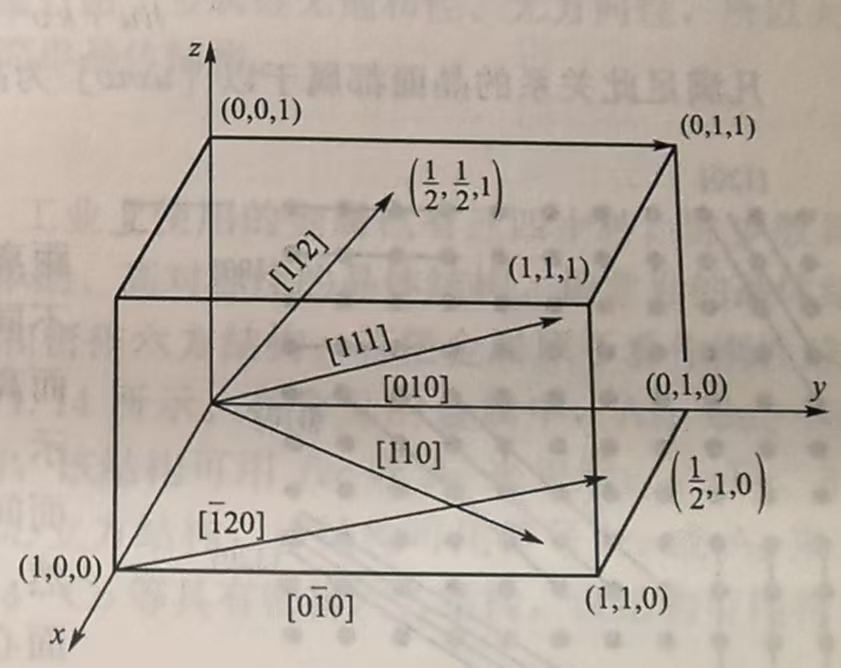
晶面指数(简称:Miller Indices)
其实前面的晶向是向量,现在求的晶面是法向量。构造过程如下:
(1)构造前面一样的坐标系,但是这次要注意把坐标系建在我们要研究的面之外,不然会出现负数,不方便计算。
(2)求出待定晶面在三个坐标轴上的截距,如果和坐标轴平行则可以记作





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








