动态网络、图信号研究相关的：Network inference from heat diffusion dynamics论文解读

1.简述

  这是一篇简短的会议论文，学术搜索Network inference from heat diffusion dynamics即可。因为课程作业需要，所以解读了这篇文章，在这里记录和分享给大家。本文将采用边翻译边解读的形式，来介绍这篇文章。

基本内容

通过热力学扩散方程式来重建网络。

背景介绍

基于图信号处理的知识，一个图信号可以通过其拉普拉斯矩阵的特征值和特征向量来表示。然后图信号处理中，基于热力学扩散的分析也逐渐受到关注。关于这个方面的研究有一篇比较经典的论文，该论文基于图像的热力学分布进行学习。这个研究也被用于处理社交网络，探索源节点分布情况等工作。并且在这些方面也已经有很成熟的研究，比如课上说的用图的拉普拉斯矩阵比较图之间的相似性，聚合一系列图信号的算法等等。

文章的创新

本文基于论文1，提出了一种通过网络稳定响应动态推断其完整连接性的方法。论文2这是一篇研究动态网络的图结构的综述性质的文章。论文3这是一篇研究如何从动态网络逆推图结构的文章，文章中提到了用动力学方面的方程组去一步步近似估计网络图结构的方法。文章这三篇文章入手进行改进，探索出了一种逆推图结构的新方法：通过观察当前图节点热扩散信号，来重建网络结构。当前热扩散信号可以被近似写成一个偏微分方程组，通过求解这个方程组就可以获得我们想要获得的图结构。常见的研究方法都是直接求解这个偏微分方程组，而这篇论文在求解这里进行了简化，使用近似估计离散的时间数值的方法，比以往的方法更加高效，因为最后可以把偏微分方程组转化为一组线性方程组，从而更高效的求解。

用到的符号：

N：节点数；E：边； V:节点；A：原图的邻接矩阵；D：度矩阵；L：拉普拉斯矩阵；$M^{†}$:伪逆矩阵；$\vec{M}$:半向量矩阵。

热力学扩散方程式

这个最早是傅里叶在研究热量在材料中的传导时发现的，这是一组偏微分方程。这组方程表面，热量在节点间的传递情况和节点组成的图拉普拉斯是成比例的。

推导：

1.由于图拉普拉斯本身就在衡量图上两个节点之间的变化，所以热扩散一定和L相关：
$$\frac{d\bar{x}(t)}{dt}=-L\bar{x}$$

从中还能得到的信息有，如果一个节点信号的向量是$1\beta$,也就是可以分割出1向量，则由于其对应L的特征值为0，故这组节点信号一定是常数，不会随着时间而改变。

2.从上面的式子积分可以获得一组线性方程,我们假设初始时候的节点信号是$x(0)$：
$$\bar{x}(t)=e^{-Lt}\bar{x}(0)$$
其中$e^{-Lt}$是一个通过矩阵指数，它由泰勒展开定义,它就是热扩散核：
$$e^{-Lt}=\sum _{n=0}^{\infty }\frac{(-Lt{)}^n}{n!}$$
3.然后我们对L进行分解为$P\Lambda P^{-1}$，可以把这个热扩散核简化为
$$e^{-Lt}=\sum _{n=0}^{\infty }\frac{(-Lt{)}^n}{n!}=P{e}^{-\Lambda t}{P}^{-1}$$
从数学角度来看这个滤波器是在递减的(因为拉普拉斯矩阵非负，所以t越大反而值越小)，也符合热扩散的定义。

5.我们的目的就是在x(t)已知的情况下逆推L，这个显然是可以实现的。

逆推图的结构

1.由于拥有节点信息，有几个节点我们是知道的，我们不知道的其实主要就是节点之间的权值，这里我们主要研究无向图，所以权值就是0或者1。我们在获得权值信息之后就可以逆推出图的连接情况。

2.传统方法：从当前的结构去求一个最优解：$minimize\Sigma ||x(t+1)-S\ast x(t)|{|}^2+正则化项$其中的S就是我们要找的近似的L。这样就把问题转换成了一个求相似的过程，这个前面上课也讲过，它是一个可微的函数，可以用求导求梯度的方式去找。在获得S之后，我们知道的是S和L相关,这里$S=e^{-Lt}$，有$S=F(L)$,所以求解L的过程就等于是求F的逆，得到$L=F^{-1}(S)$。

3.文章提出的方法：直接从$\frac{d\bar{x}(t)}{dt}=-L\bar{x}$入手解决。

具体思路：

1.如何获得可以求解L的线性方程组

1.我们不从0时刻开始，而是根据前面的方程，用连续时间导数进行近似到任一时刻开始：
$$\frac{d\vec{x}(t)}{dt}\approx \frac{\Delta \vec{x}}{\Delta t}=\frac{\vec{x}(t_{i+1})-\vec{x}(t_i)}{t_{i+1}-t_i}\approx -L\cdot \vec{x}(t_i)$$
这里要求$\Delta t=|t_{i+1}-t_i|$足够小，对应的就是采样的间隔要小，保证图信号的变换只和时间相关，其实就是求了个导数。

2.在均匀的$\Delta t$上进行采样：获得$X=[{\vec{x}}_1{\vec{x}}_2\dots {\vec{x}}_{M+1}]$,其中$x_i\equiv \vec{x}(t_i)$。

3.根据采样到的信息，我们引入两个矩阵$V = [\vec{v}_1 \quad \vec{v}_2 \quad \ldots \quad \vec{v}_M] \quad $和$\quad U = [\vec{u}_1 \quad \vec{u}_2 \quad \ldots \quad \vec{u}_M]$.其中$\vec{u}_i = -\vec{x}_i$，$\vec{v}i = \frac{1}{\Delta t} (\vec{x}{i+1} - \vec{x}_i)$.

4.然后，上面的方程就可以变成：$L\cdot {\vec{u}}_i={\vec{v}}_i$.

5.因为是我们采样到的信息，所以U和V的值我们其实都是已知的，唯一不知道的只有L的值。

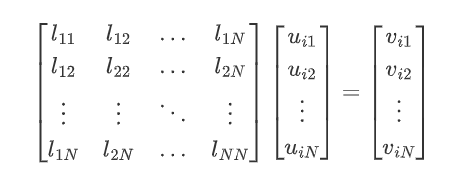
6.然后还是线性代数的东西：L具有对称性，所以L里面自由变量的数量是$N_S=\frac{N(N+1)}{2}$。通过对矩阵进行半向量化就可以提取自由变量，$\mathbf{l}=\mathrm{vech}(L)$，简单来说就是取它的上三角或者下三角元素排成一个向量。然后，我们就可以把公式变成：
$$U_i\vec{l}={\vec{v}}_i$$
其中U是一个NxN的矩阵，简单来说，$U$ 是一个由输入向量 $\vec{u}$ 的元素重新排列组成的“系数矩阵”：
$${\mathbf{U}}_i={\left[\begin{array}{c}{0}_{k-1\times N-k+1}\\ u_i((k:N))\\ \begin{array}{cc}{0}_{N-k\times 1}& u_i(k)I_{N-k}\end{array}\end{array}\right]}_{k=1}^N$$
这里看似很复杂，但是举个简单的例子就可以说明：

(1)假设 $L$ 是一个 $2\times 2$ 的对称矩阵：

$$L=[\begin{array}{c}l\end{array}$$