NSGA2遗传算法实现多目标优化问题的三维视图分析：帕累托前沿图与最终结果，NSGA2遗传算法实现多目标优化问题的三维视图及结果分析

NSGA2遗传算法多目标优化 三维视图
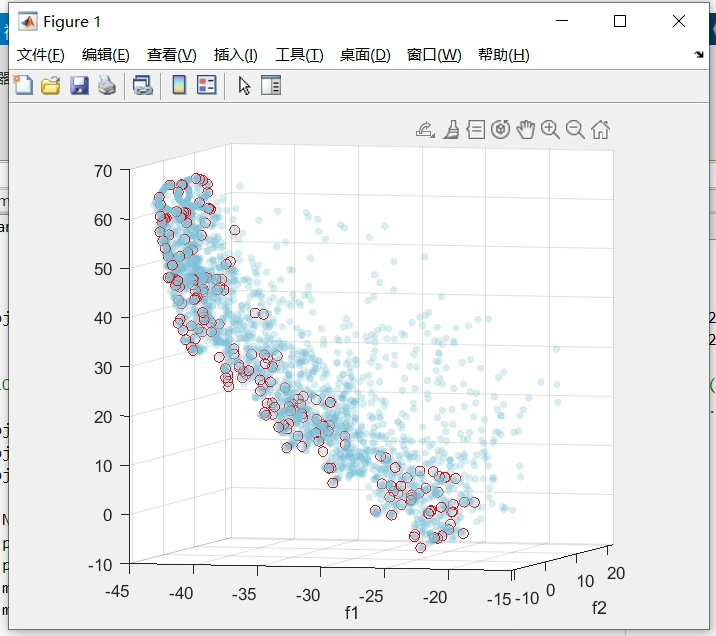
寻优多个函数（函数类型见图二类型），出图为三维红色为帕列托（图一），
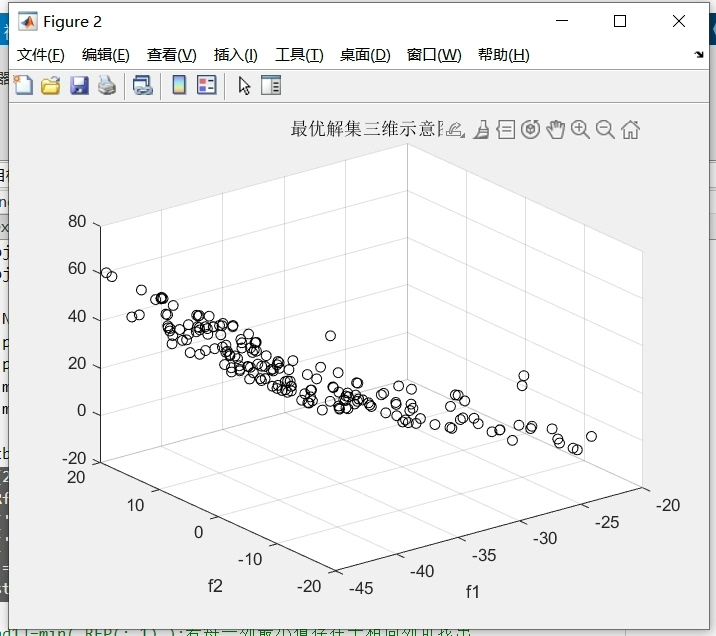
带最终结果图（图三）

ID:7112755798166967

豆豆hchc

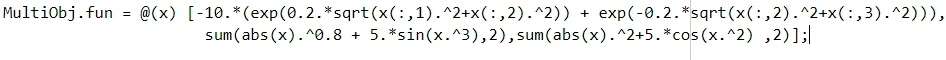
NSGA2遗传算法多目标优化是一种常用的优化算法，它通过模拟生物进化的过程来寻找多个目标函数的最优解。在这篇文章中，我们将重点探讨如何利用NSGA2遗传算法进行三维视图的优化。

首先，让我们来了解一下NSGA2遗传算法的基本原理。遗传算法是一种模拟进化的优化算法，它通过不断迭代的方式来逐步优化解的质量。在NSGA2遗传算法中，每个解都可以看作是一个个体，而每个个体都有一组基因，这些基因代表了解的各个属性。通过交叉和变异等遗传操作，我们可以生成新的个体，并对它们进行评估。根据评估结果，我们可以选择一部分优秀的个体作为下一代的父代，并继续进行遗传操作，直到达到停止条件。

在多目标优化中，我们需要同时优化多个目标函数。在这篇文章中，我们选择了一组函数（函数类型见图二类型），并将其视为我们的目标函数。为了更直观地展示优化结果，我们引入了三维视图，并将优化结果以三维红色帕雷托图的形式进行展示（图一）。这样一来，每个解都可以表示为三维空间中的一个点，而优秀的解则可以体现为图中的红色区域。

为了实现NSGA2遗传算法的多目标优化，我们需要定义适应度函数。在这里，我们可以将适应度函数定义为目标函数的加权和，其中权重可以根据实际需求进行调整。通过适应度函数的计算，我们可以对个体进行排名，以确定优秀个体的选择概率。NSGA2遗传算法中的主要思想是维持一定的多样性，因此在选择优秀个体时，我们不仅考虑了适应度函数的大小，还考虑了个体之间的关系。具体来说，我们使用了快速非支配排序算法将个体划分为不同的等级，优先选择非支配解，并保持一定的平衡，以避免局部最优解的困扰。

在优化过程中，我们不断迭代，直到达到停止条件。在每一代中，我们根据交叉和变异等操作，生成新的个体，并通过适应度函数进行排序和选择。通过选择操作，我们得到下一代的父代，并继续进行遗传操作。通过这样的迭代过程，我们逐步逼近最优解，并将其表示为三维视图中的红色区域。

最终，我们得到了优化结果，并将其以图三的形式展示出来。图三展示了经过NSGA2遗传算法优化后的最终解，其中红色区域表示优秀解的集合。通过这样的三维视图，我们可以更直观地了解优化结果，并进行进一步的分析和决策。

综上所述，本文围绕NSGA2遗传算法多目标优化的三维视图展开阐述。我们介绍了NSGA2遗传算法的基本原理，以及在多目标优化中的应用。通过引入适应度函数和优良个体选择策略，我们能够在优化过程中保持一定的多样性，并逐步逼近最优解。最后，我们通过三维视图展示了优化结果，以供进一步的分析和决策。希望本文对读者在NSGA2遗传算法多目标优化方面的研究提供帮助和借鉴。

以上相关代码,程序地址：http://fansik.cn/755798166967.html