第7章 梯度下降法和牛顿法（算法原理+手编实现）

---

俯视机器学习

---

有了梦寐以求的知识，是否就算是拥有春天！

---

第7章 梯度下降法和牛顿法

1. 迭代法框架

算法1：广义下降法

• 给定起始点 $x\in \mathrm{d}\mathrm{o}\mathrm{m}f$
• 循环
  1. 选择下降方向 $\Delta x$.
  2. 确定搜索步长 $t>0$.
  3. 更新. $x:=x+t\Delta x$
• 直到满足结束条件

2. 精确线搜索

目的：确定 $t$。取
$$t^{\prime }=\underset{t\ge 0}{\mathrm{argmin}}f(x+t\Delta x)\text{\hspace{1em}(1)}$$
即为最佳值。

3. 回溯线搜索

回溯线搜索（Backtracking line search）是一种不精确的线搜索方法，具体如下

算法2：回溯线搜索

• 给定初始点 $x\in \mathrm{d}\mathrm{o}\mathrm{m}\mathrm{f}$ 、下降方向 $\Delta x$，$\alpha \in (0,0.5),\beta \in (0,1),t=1$。
• while $f(x+t\Delta x)>f(x)+\alpha t\nabla f(x{)}^T\Delta x$
  • $t:=\beta t$

4. 梯度下降法

关键：增量 $\Delta x=-\nabla f(x)$。

算法3：梯度下降法

• 给定起始点 $x\in \mathrm{d}\mathrm{o}\mathrm{m}f$.
• 重复
  1. $\Delta x:=-\nabla f(x)$.
  2. 线搜索，确定步长 $t$.
  3. 更新, $x:=x+t\Delta x$.
• 直到满足停止条件。

停止条件可根据需要设定，一种常见方法为：
给定一个较小值 $ϵ$，
$$\Vert \nabla f(x){\Vert }_2\le ϵ$$
时停止。

5. 牛顿法推导

对 $f(x),x\in R^n$，可在 $x^{(k)}$ 处作二阶泰勒展开
$$f(x)=f(x^{(k)})+\nabla f(x^{(k)}{)}^T(x-x^{(k)})+\frac{1}{2}(x-x^{(k)}{)}^T{\nabla }^{2}f(x^{(k)}))(x-x^{(k)})+o(\Vert x-x^{(k)}{\Vert }^2)$$
忽略高阶无穷小，有
$$f(x)\approx f(x^{(k)})+\nabla f(x^{(k)}{)}^T(x-x^{(k)})+\frac{1}{2}(x-x^{(k)}{)}^T{\nabla }^{2}f(x^{(k)}))(x-x^{(k)})$$
则
$$\nabla f(x)=\nabla f(x^{(k)})+{\nabla }^{2}f(x^{(k)})(x-x^{(k)})$$
令 $\nabla f(x)=0$，解得
$$x^{(k+1)}=x^{(k)}-[{\nabla }^{2}f(x^{(k)}){]}^{-1}\nabla f(x^{(k)})\text{\hspace{1em}(1)}$$
公式 $(1)$ 即为更新公式。

​ 牛顿法采用二阶近似（例如：一维时采用二次函数近似，对于二次函数优化问题，可以一次迭代获得最优解），联系迭代法框架，这里相当于每次迭代步长取 $1$， 优化方向取 $-[{\nabla }^{2}f(x^{(k)}){]}^{-1}\nabla f(x^{(k)})$ 。

6. 编程实现梯度下降法，并求解简单二次规划问题

求下面二元函数最小值点：
$$f(x)=\frac{1}{2}(x_1^2+10x_2^2)=\frac{1}{2}[x_1,x_2]\left[\begin{array}{cc}1& 0\\ 0& 10\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\frac{1}{2}{x}^{T}Ax$$
其中 $x\in R^2$ 。

条件数（矩阵最大特征值与最小特征值之比）为 10。其一阶导数、二阶导数分别为
$$\begin{gathered} \nabla f=Ax \\ {\nabla }^{2}f=A \end{gathered}$$

步长搜索分别用精确线搜索和不精确线搜索（回溯法）两种方式。

import numpy as np
import matplotlib.pyplot as plt

def draw(xs, save_path=""):
    xx1 = np.linspace(-12, 12, 200)
    xx2 = np.linspace(-5, 5, 200)
    xx1, xx2 = np.meshgrid(xx1, xx2)

    z = 1/2 * (xx1**2 + 10 * xx2**2)

    plt.figure(figsize=(8,4))
    plt.xlim([-12, 12])
    plt.ylim([-5, 5])
    plt.contour(xx1, xx2, z)

    # 关键行
    plt.plot(xs[:,0], xs[:,1], 'ro', xs[:,0], xs[:,1], 'k--')
    if save_path:
        plt.savefig(save_path)
    plt.show()
    
    
x0 = np.array([10, 2]) # 初始点
A  = np.array([[1, 0], [0, 10]])
ep = 1e-5

def f(x):
    return 1/2 * (x.T @ A @ x)

def grad(x):
    return A @ x

def hessian(x):
    return A

def get_exact_t(x, dx):
    t = -dx.T @ A @ x / (dx.T @ A @ dx)
    return t 
    
def get_inexact_t(x, dx, a=0.1, b=0.9):
    t = 1.
    while f(x + t*dx) > f(x) + a*t*(grad(x).T @ dx):
        t = b * t
    return t

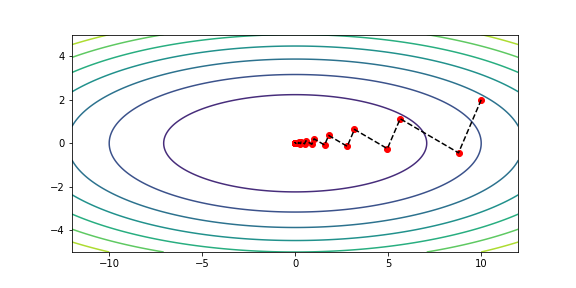
# 梯度下降法：精确线搜索
n1 = 0 # 迭代次数
x = x0
xs1 = [x]
while np.linalg.norm(grad(x)) > ep:
    dx = -grad(x)
    t  = get_exact_t(x, dx)
    x  = x + t * dx
    xs1.append(x)
    n1 += 1

print(f'Exact line search, iterate {n1} times.')
xs1 = np.array(xs1)
draw(xs1)

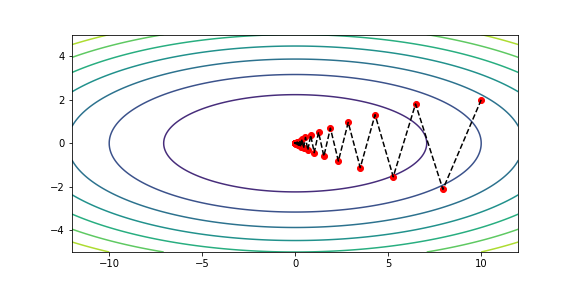
# 梯度下降法：不精确线搜索
n2 = 0 # 迭代次数
x = x0
xs2 = [x]
while np.linalg.norm(grad(x)) > ep:
    dx = -grad(x)
    t  = get_inexact_t(x, dx)
    x  = x + t * dx
    xs2.append(x)
    n2 += 1
    
print(f'Inexact line search, iterate {n2} times.')

xs2 = np.array(xs2)
draw(xs2)

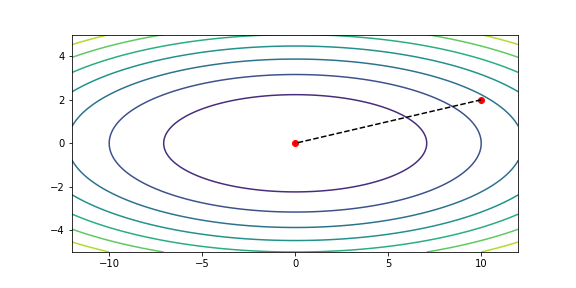
7. 编程实现牛顿法，并求解简单二次规划问题

# 牛顿法
n3 = 0 # 迭代次数
x = x0
xs3 = [x]
while np.linalg.norm(grad(x)) > ep:
    dx = -np.linalg.inv(hessian(x)) @ grad(x)
    x  = x + dx
    xs3.append(x)
    n3 += 1
    
print(f'Newtons method, iterate {n3} times.')

xs3 = np.array(xs3)
draw(xs3)

---

版权申明：本教程版权归创作人所有，未经许可，谢绝转载！

---

---

交流讨论QQ群：784117704

部分视频观看地址：b站搜索“火力教育”

课件下载地址：QQ群文件（有最新更新） or 百度网盘PDF课件及代码

链接：https://pan.baidu.com/s/1lc8c7yDc30KY1L_ehJAfDg
提取码：u3ls

---