代码随想录Day16 513.找树左下角的值，112. 路径总和，113. 路径总和ii,106.从中序与后序遍历序列构造二叉树,105.从前序与中序遍历序列构造二叉树。

最新推荐文章于 2025-10-29 13:01:20 发布

原创最新推荐文章于 2025-10-29 13:01:20 发布 · 972 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #java #笔记 #算法 #开发语言

代码随想录训练营同时被 3 个专栏收录

52 篇文章

订阅专栏

二叉树

10 篇文章

订阅专栏

队列

10 篇文章

订阅专栏

1.找树左下角的值

给定一个二叉树，在树的最后一行找到最左边的值。

示例 1:

513.找树左下角的值

示例 2:

513.找树左下角的值1

思路

本题要找出树的最后一行的最左边的值。此时大家应该想起用层序遍历是非常简单的了，反而用递归的话会比较难一点。

递归

咋眼一看，这道题目用递归的话就就一直向左遍历，最后一个就是答案呗？

没有这么简单，一直向左遍历到最后一个，它未必是最后一行啊。

分析一下题目：在树的最后一行找到最左边的值。

首先要是最后一行，然后是最左边的值。

如果使用递归法，如何判断是最后一行呢，其实就是深度最大的叶子节点一定是最后一行。

如果对二叉树深度和高度还有点疑惑的话，请看：110.平衡二叉树 (opens new window)。

所以要找深度最大的叶子节点。

那么如何找最左边的呢？可以使用前序遍历（当然中序，后序都可以，因为本题没有中间节点的处理逻辑，只要左优先就行），保证优先左边搜索，然后记录深度最大的叶子节点，此时就是树的最后一行最左边的值。

递归三部曲：

确定递归函数的参数和返回值

参数必须有要遍历的树的根节点，还有就是一个int型的变量用来记录最长深度。这里就不需要返回值了，所以递归函数的返回类型为void。

本题还需要类里的两个全局变量，maxLen用来记录最大深度，result记录最大深度最左节点的数值。

确定终止条件

当遇到叶子节点的时候，就需要统计一下最大的深度了，所以需要遇到叶子节点来更新最大深度。

确定单层递归的逻辑

在找最大深度的时候，递归的过程中依然要使用回溯

迭代法

本题使用层序遍历再合适不过了，比递归要好理解得多！

只需要记录最后一行第一个节点的数值就可以了。

如果对层序遍历不了解，看这篇二叉树：层序遍历登场！ (opens new window)，这篇里也给出了层序遍历的模板，稍作修改就一过刷了这道题了。

总结

本题涉及如下几点：

递归求深度的写法，我们在110.平衡二叉树 (opens new window)中详细的分析了深度应该怎么求，高度应该怎么求。
递归中其实隐藏了回溯，在257. 二叉树的所有路径 (opens new window)中讲解了究竟哪里使用了回溯，哪里隐藏了回溯。
层次遍历，在二叉树：层序遍历登场！ (opens new window)深度讲解了二叉树层次遍历。所以本题涉及到的点，我们之前都讲解过，这些知识点需要同学们灵活运用，这样就举一反三了。

递归

public class Find_the_Value_at_the_Bottom_Left_of_the_Tree {
    private int Deep = -1;
    private int value = 0;
    public int findBottomLeftValue1(TreeNode root) {
        value = root.val;
        findLeftValue(root,0);//从根节点开始,深度为0
        return value;
    }
    private void findLeftValue (TreeNode root,int deep) {
        if (root == null) return;
        if (root.left == null && root.right == null) {//当前节点是叶子结点,且深度大于之前记录的深度
            if (deep > Deep) {
                value = root.val;//更新最底层最左边节点值和深度
                Deep = deep;
            }
        }
        if (root.left != null) findLeftValue(root.left,deep + 1);//左右子节点不为空,递归查找左右子节点
        if (root.right != null) findLeftValue(root.right,deep + 1);
    }
}

时间复杂度: O(n)

空间复杂度: O(n)（最坏情况）或 O(log n)（最好情况）

迭代

public class Find_the_Value_at_the_Bottom_Left_of_the_Tree {
  public int findBottomLeftValue2(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int res = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode poll = queue.poll();//offer(1)：队列变为[1]2. offer(2)：队列变为[1, 2]3. poll()：移除并返回1，队列变为[2]
                if (i == 0) {//在每一层中，第一个被poll出来的节点是最左边的节点。
                    res = poll.val;
                }
                if (poll.left != null) {
                    queue.offer(poll.left);
                }
                if (poll.right != null) {
                    queue.offer(poll.right);
                }
            }
        }
        return res;
    }
}

时间复杂度: O(n)

空间复杂度: O(n)（最坏情况）或 O(h)（最好情况，链状树的情况）

2.路径总和

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例: 给定如下二叉树，以及目标和 sum = 22，

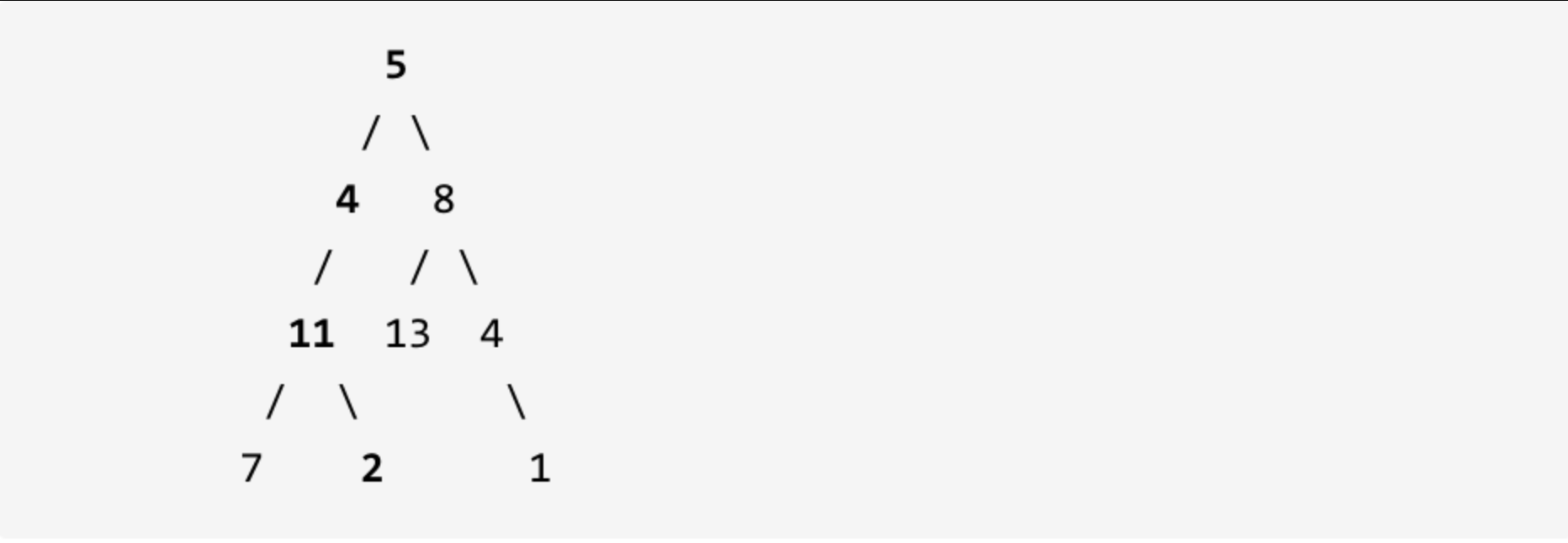
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

思路

相信很多同学都会疑惑，递归函数什么时候要有返回值，什么时候没有返回值，特别是有的时候递归函数返回类型为bool类型。

那么接下来我通过详细讲解如下两道题，来回答这个问题：

这道题我们要遍历从根节点到叶子节点的路径看看总和是不是目标和。

递归

可以使用深度优先遍历的方式（本题前中后序都可以，无所谓，因为中节点也没有处理逻辑）来遍历二叉树

确定递归函数的参数和返回类型

参数：需要二叉树的根节点，还需要一个计数器，这个计数器用来计算二叉树的一条边之和是否正好是目标和，计数器为int型。

再来看返回值，递归函数什么时候需要返回值？什么时候不需要返回值？这里总结如下三点：

如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（这种情况就是本文下半部分介绍的113.路径总和ii）
如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。（这种情况我们在236. 二叉树的最近公共祖先 (opens new window)中介绍）
如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（本题的情况）

而本题我们要找一条符合条件的路径，所以递归函数需要返回值，及时返回，那么返回类型是什么呢？

如图所示：

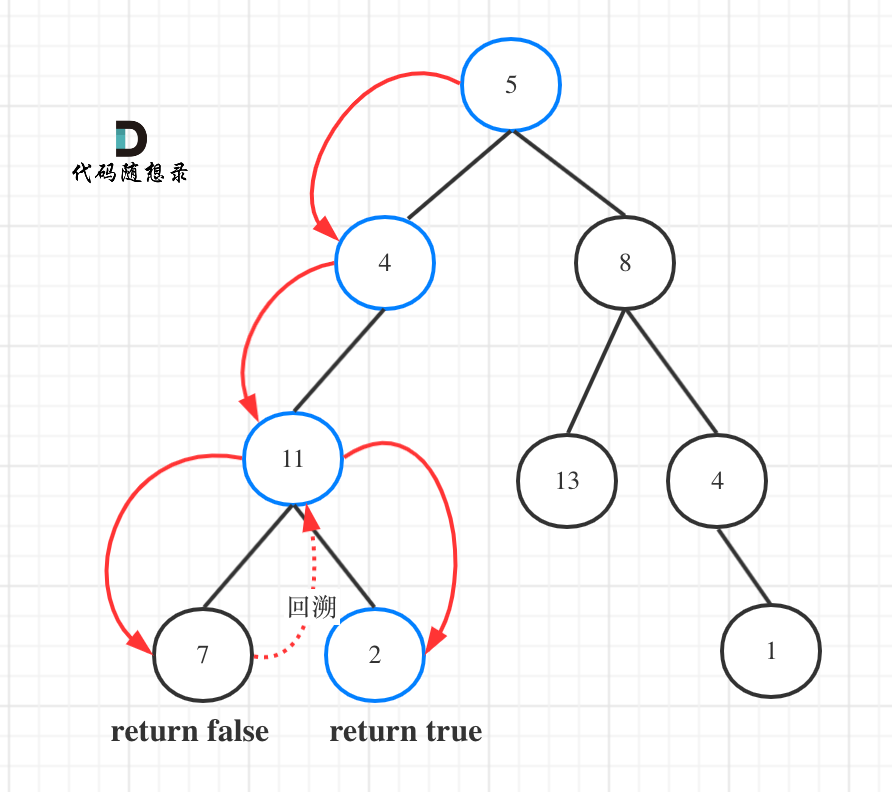
112.路径总和

图中可以看出，遍历的路线，并不要遍历整棵树，所以递归函数需要返回值，可以用bool类型表示。

确定终止条件

首先计数器如何统计这一条路径的和呢？

不要去累加然后判断是否等于目标和，那么代码比较麻烦，可以用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。

如果最后count == 0，同时到了叶子节点的话，说明找到了目标和。

如果遍历到了叶子节点，count不为0，就是没找到。

确定单层递归的逻辑

因为终止条件是判断叶子节点，所以递归的过程中就不要让空节点进入递归了。

递归函数是有返回值的，如果递归函数返回true，说明找到了合适的路径，应该立刻返回。

迭代

如果使用栈模拟递归的话，那么如果做回溯呢？

此时栈里一个元素不仅要记录该节点指针，还要记录从头结点到该节点的路径数值总和。

递归

public class Path_Sum {
    public boolean haspathsum1(TreeNode root, int targetsum) {
        if (root == null) return false;
        if (root.left == null && root.right == null) return root.val == targetsum;//当前节点是叶子节点（即没有左右子节点），检查当前节点的值是否等于targetSum。
        return haspathsum1(root.left, targetsum - root.val) || haspathsum1(root.right, targetsum - root.val);//如果当前节点不是叶子节点，递归地检查左子树和右子树,将目标路径和减去当前节点的值，因为当前节点的值已经是路径的一部分了。
    }
}

时间复杂度: O(n)

空间复杂度: O(n)（最坏情况）或 O(log n)（最好情况)

迭代

public class Path_Sum { 
public boolean haspathsum2(TreeNode root, int targetsum) {
        if (root == null) return false;
        Stack<TreeNode> stack1 = new Stack<>();//储存树的节点
        Stack<Integer> stack2 = new Stack<>();//储存当前路径的和
        stack1.push(root);
        stack2.push(root.val);
        while (!stack1.isEmpty()) {
            int size = stack1.size();
            for (int i = 0; i < size; i++) {//对于每个节点，从stack1中弹出一个节点，并从stack2中弹出对应的路径和。
                TreeNode node = stack1.pop();
                int sum = stack2.pop();
                if (node.left == null && node.right == null && sum == targetsum) {//// 如果该节点是叶子节点了，同时该节点的路径数值等于sum，那么就返回true
                    return true;
                }
                // 右节点，压进去一个节点的时候，将该节点的路径数值也记录下来
                if (node.right != null) {
                    stack1.push(node.right);
                    stack2.push(sum + node.right.val);
                }
                // 左节点，压进去一个节点的时候，将该节点的路径数值也记录下来
                if (node.left != null) {
                    stack1.push(node.left);
                    stack2.push(sum + node.left.val);
                }
            }
        }
        return false;
    }
}

时间复杂度: O(n)

空间复杂度: O(h)（最坏情况是 O(n)，对于链状树）

public class Path_Sum {  
public boolean hasPathSum3(TreeNode root, int targetSum) {
        Stack<TreeNode> treeNodeStack = new Stack<>();//储存树的节点
        Stack<Integer> sumStack = new Stack<>();
        if (root == null)
            return false;
        treeNodeStack.add(root);
        sumStack.add(root.val);
        while (!treeNodeStack.isEmpty()) {
            TreeNode curr = treeNodeStack.peek();//查看栈顶节点curr，同时从sumStack中弹出对应的路径和
            int tempsum = sumStack.pop();
            if (curr != null) {//如果curr不为空，将其从treeNodeStack中弹出，并重新压入栈中，以便在下一次循环中处理其子节点。同时，压入一个null作为分隔符，用于区分不同层级的节点
                treeNodeStack.pop();
                treeNodeStack.add(curr);
                treeNodeStack.add(null);
                sumStack.add(tempsum);
                if (curr.right != null) {//对于curr的左右子节点，如果它们不为空，将它们及其对应的路径和压入栈中。
                    treeNodeStack.add(curr.right);
                    sumStack.add(tempsum + curr.right.val);
                }
                if (curr.left != null) {
                    treeNodeStack.add(curr.left);
                    sumStack.add(tempsum + curr.left.val);
                }
            } else {//如果curr为空，表示已经处理完一层的节点，此时弹出null分隔符和下一个节点temp。检查temp是否是叶子节点（没有左右子节点），并且路径和tempsum是否等于目标和targetSum。如果是，返回true。
                treeNodeStack.pop();
                TreeNode temp = treeNodeStack.pop();
                if (temp.left == null && temp.right == null && tempsum == targetSum)
                    return true;
            }
        }
        return false;
    }
}

时间复杂度: O(n)

空间复杂度: O(h)（最坏情况是 O(n)，对于链状树）

3.路径总和ii

给定一个二叉树和一个目标和，找到所有从根节点到叶子节点路径总和等于给定目标和的路径。

说明: 叶子节点是指没有子节点的节点。

示例: 给定如下二叉树，以及目标和 sum = 22，

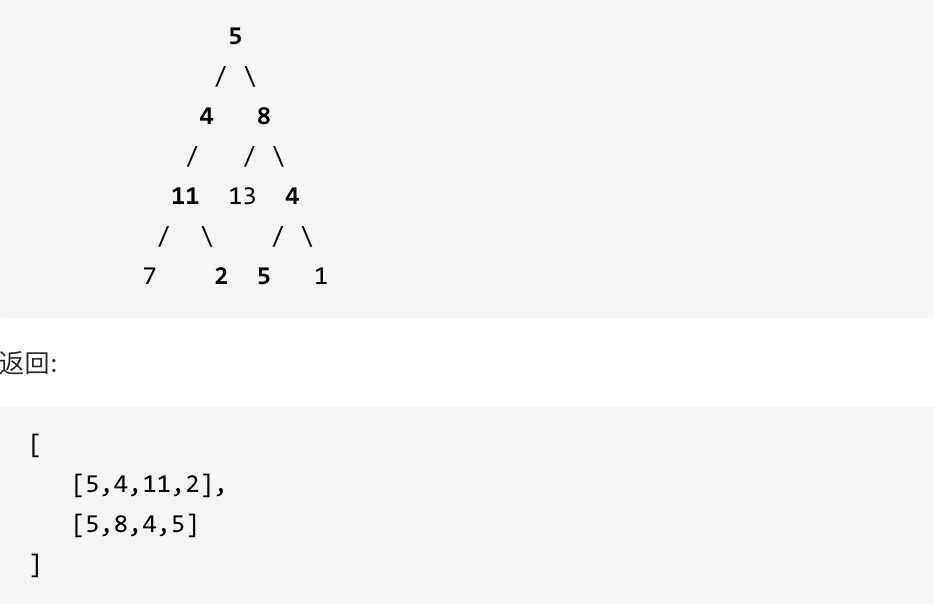
113.路径总和ii1.png

思路

113.路径总和ii要遍历整个树，找到所有路径，所以递归函数不要返回值！

如图：

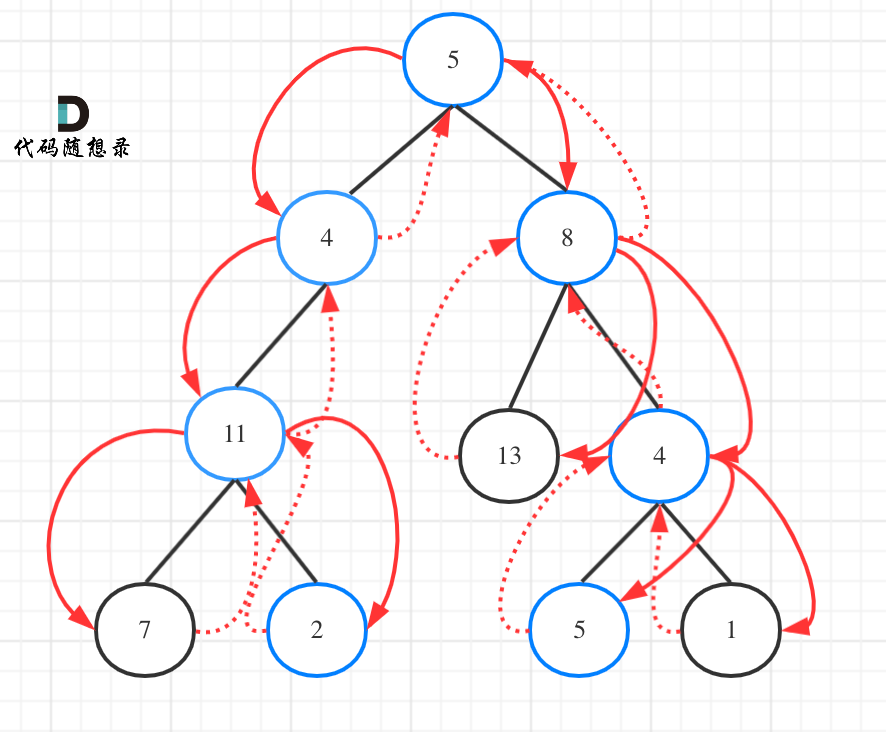
113.路径总和ii

总结

本篇通过leetcode上112. 路径总和和 113. 路径总和ii 详细的讲解了递归函数什么时候需要返回值，什么不需要返回值。

这两道题目是掌握这一知识点非常好的题目，大家看完本篇文章再去做题，就会感受到搜索整棵树和搜索某一路径的差别。

对于112. 路径总和，我依然给出了递归法和迭代法，这种题目其实用迭代法会复杂一些，能掌握递归方式就够了！

递归

public class Path_Sum_II {
    List<List<Integer>> result;//储存所有满足条件的路径
    LinkedList<Integer> path;//储存当前正在探索的路径
    public List<List<Integer>> pathSum (TreeNode root,int targetSum) {
        result = new LinkedList<>();
        path = new LinkedList<>();
        travesal(root, targetSum);
        return result;
    }
    private void travesal(TreeNode root,  int count) {
        if (root == null) return;
        path.offer(root.val);
        count -= root.val;//更新为剩余需要的和
        if (root.left == null && root.right == null && count == 0) {//如果当前节点是叶子节点（没有左右子节点），并且剩余需要的和count为0，则将当前路径添加到result中。
            result.add(new LinkedList<>(path));
        }
        travesal(root.left, count);
        travesal(root.right, count);
        path.removeLast();//在返回之前，从path中移除当前节点的值，实现回溯。
    }
}

时间复杂度:O(n)

空间复杂度: O(n)（最坏情况）或 O(h)（最好情况）

迭代

public class Path_Sum_II {   
 public List<List<Integer>> pathsum(TreeNode root, int targetsum) {
        List<List<Integer>> res = new ArrayList<>();//储存所有满足条件的路径
        if (root == null) return res;
        List<Integer> path = new LinkedList<>();//储存当前正在探索的路径
        preorderdfs(root, targetsum, res, path);
        return res;
    }

    public void preorderdfs(TreeNode root, int targetsum, List<List<Integer>> res, List<Integer> path) {
        path.add(root.val);
        if (root.left == null && root.right == null) {//当前节点是叶子节点（没有左右子节点），检查当前路径的和是否等于targetsum。如果相等，将当前路径添加到res中。
            if (targetsum - root.val == 0) {
                res.add(new ArrayList<>(path));
            }
            return;
        }
        if (root.left != null) {//如果当前节点有左子节点，递归调用preorderdfs方法探索左子树，并在返回后进行回溯（从path中移除当前节点的值）。
            preorderdfs(root.left, targetsum - root.val, res, path);
            path.remove(path.size() - 1);
        }
        if (root.right != null) {
            preorderdfs(root.right, targetsum - root.val, res, path);
            path.remove(path.size() - 1);
        }
    }
}

时间复杂度: O(n)

空间复杂度: O(n)（最坏情况）或 O(h)（最好情况）

public class Path_Sum_II {    
public List<List<Integer>> pathSum2(TreeNode root, int targetSum) {
        List<List<Integer>> result = new ArrayList<>();//储存所有满足条件的路径
        Stack<TreeNode> nodeStack = new Stack<>();//储存节点
        Stack<Integer> sumStack = new Stack<>();//储存路径和
        Stack<ArrayList<Integer>> pathStack = new Stack<>();//储存路径
        if(root == null)
            return result;
        nodeStack.add(root);//根节点不为空时，将根节点、其值和空路径压入栈中。
        sumStack.add(root.val);
        pathStack.add(new ArrayList<>());
        while(!nodeStack.isEmpty()){//弹出栈顶节点currNode、对应的路径和currSum和对应的路径currPath。
            TreeNode currNode = nodeStack.peek();
            int currSum = sumStack.pop();
            ArrayList<Integer> currPath = pathStack.pop();
            if(currNode != null){//如果currNode不为空，处理当前节点
                nodeStack.pop();
                nodeStack.add(currNode);//再次添加当前节点，为了处理子节点
                nodeStack.add(null);// 添加一个空节点作为分隔符
                sumStack.add(currSum);
                currPath.add(currNode.val);
                pathStack.add(new ArrayList(currPath));// 复制当前路径，为子节点做准备
                if(currNode.right != null){//有右子节点，将其添加到nodeStack，更新路径和并复制当前路径。
                    nodeStack.add(currNode.right);
                    sumStack.add(currSum + currNode.right.val);
                    pathStack.add(new ArrayList(currPath));
                }
                if(currNode.left != null){
                    nodeStack.add(currNode.left);
                    sumStack.add(currSum + currNode.left.val);
                    pathStack.add(new ArrayList(currPath));
                }
            }else {//如果currNode为空，表示已经处理完一层的节点
                nodeStack.pop();//弹出null分隔符和下一个节点temp。
                TreeNode temp = nodeStack.pop();
                if (temp.left == null && temp.right == null && currSum == targetSum) {//如果temp是叶子节点且currSum等于targetSum，则将currPath添加到结果列表result中。
                    result.add(new ArrayList(currPath));
                }
            }
        }
        return result;
    }
}

时间复杂度: O(n)

空间复杂度: O(n)（最坏情况）或 O(h)（最好情况）

4.从中序与后序遍历序列构造二叉树

根据一棵树的中序遍历与后序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树：

106. 从中序与后序遍历序列构造二叉树1

思路

首先回忆一下如何根据两个顺序构造一个唯一的二叉树，相信理论知识大家应该都清楚，就是以后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。

如果让我们肉眼看两个序列，画一棵二叉树的话，应该分分钟都可以画出来。

流程如图：

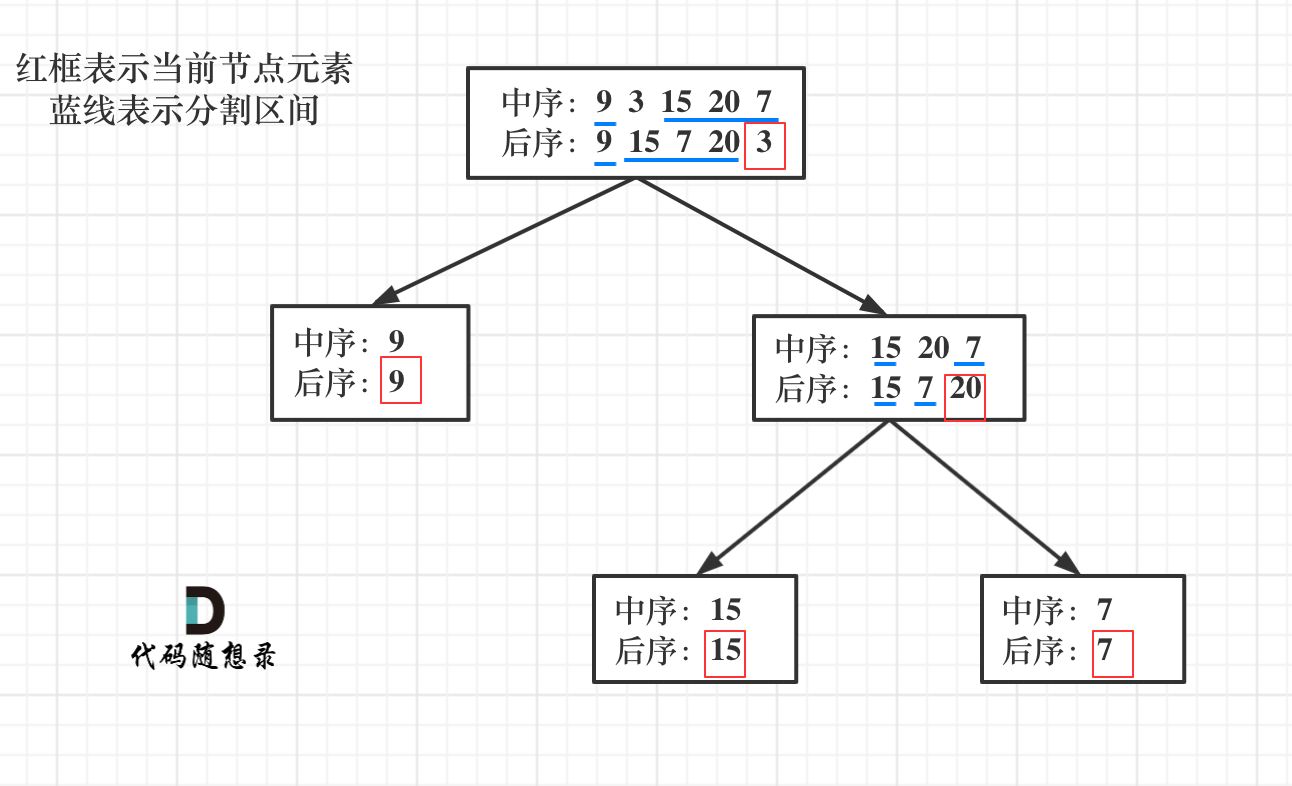
106.从中序与后序遍历序列构造二叉树

一层一层切割，就应该想到了递归。

来看一下一共分几步：

第一步：如果数组大小为零的话，说明是空节点了。
第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
第四步：切割中序数组，切成中序左数组和中序右数组（顺序别搞反了，一定是先切中序数组）
第五步：切割后序数组，切成后序左数组和后序右数组
第六步：递归处理左区间和右区间

难点大家应该发现了，就是如何切割，以及边界值找不好很容易乱套。

此时应该注意确定切割的标准，是左闭右开，还有左开右闭，还是左闭右闭，这个就是不变量，要在递归中保持这个不变量。

在切割的过程中会产生四个区间，把握不好不变量的话，一会左闭右开，一会左闭右闭，必然乱套！

我在数组：每次遇到二分法，都是一看就会，一写就废 (opens new window)和数组：这个循环可以转懵很多人！ (opens new window)中都强调过循环不变量的重要性，在二分查找以及螺旋矩阵的求解中，坚持循环不变量非常重要，本题也是。

首先要切割中序数组，为什么先切割中序数组呢？

切割点在后序数组的最后一个元素，就是用这个元素来切割中序数组的，所以必要先切割中序数组。

中序数组相对比较好切，找到切割点（后序数组的最后一个元素）在中序数组的位置，然后切割。

切割后序数组，首先后序数组的最后一个元素指定不能要了，这是切割点也是当前二叉树中间节点的元素，已经用了。

后序数组的切割点怎么找？

后序数组没有明确的切割元素来进行左右切割，不像中序数组有明确的切割点，切割点左右分开就可以了。

此时有一个很重的点，就是中序数组大小一定是和后序数组的大小相同的（这是必然）。

中序数组我们都切成了左中序数组和右中序数组了，那么后序数组就可以按照左中序数组的大小来切割，切成左后序数组和右后序数组。

此时，中序数组切成了左中序数组和右中序数组，后序数组切割成左后序数组和右后序数组。

接下来可以递归了。

public class Constructing_a_Binary_Tree_from_Inorder_and_Postorder_Traversal_Sequences {
    Map<Integer, Integer> map;//存储中序遍历序列中每个数值对应的索引位置
    public TreeNode buildTree1(int[] inorder, int[] postorder) {//inorder表示中序遍历序列，postorder表示后序遍历序列
        map = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) { // 用map保存中序序列的数值对应位置
            map.put(inorder[i], i);
        }
        return findNode(inorder,  0, inorder.length, postorder,0, postorder.length);  //调用方法重建二叉树 前闭后开
    }

    public TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd) {//接受六个参数：中序遍历序列的数组，中序遍历序列的当前子树的起始和结束索引，前闭后开，后序遍历的数组，后序遍历序列的当前子树的起始和结束索引，前闭后开
        if (inBegin >= inEnd || postBegin >= postEnd) {//如果中序或后序遍历序列的索引超出范围，说明当前子树为空
            return null;
        }
        int rootIndex = map.get(postorder[postEnd - 1]);//在后序遍历中，最后一个元素是根节点。通过map查找这个根节点在中序遍历序列中的索引rootIndex。
        TreeNode root = new TreeNode(inorder[rootIndex]);//根据中序遍历序列中的根节点值构造根节点。
        int lenOfLeft = rootIndex - inBegin;//计算根节点的左子树在中序遍历中的大小，rootIndex是根节点在中序遍历中的索引，inBegin是当前正在处理的中序子数组的起始索引。两者之差即为左子树中的节点数量。
        root.left = findNode(inorder, inBegin, rootIndex,
                postorder, postBegin, postBegin + lenOfLeft);//递归构建左子树，inBegin和rootIndex：左子树在中序遍历中的范围。postBegin和postBegin + lenOfLeft：左子树在后序遍历中的范围。
        root.right = findNode(inorder, rootIndex + 1, inEnd,
                postorder, postBegin + lenOfLeft, postEnd - 1);//递归构建右子树，rootIndex + 1和inEnd：右子树在中序遍历中的范围，从根节点的下一个节点开始，直到子数组的末尾。postBegin + lenOfLeft和postEnd - 1：右子树在后序遍历中的范围，从左子树的后序遍历结束的下一个节点开始，直到子数组的末尾。
        return root;
    }
}

时间复杂度: O(n)

空间复杂度: O(n)

public class Constructing_a_Binary_Tree_from_Inorder_and_Postorder_Traversal_Sequences {    
public TreeNode buildTree2(int[] inorder, int[] postorder) {
        if(postorder.length == 0 || inorder.length == 0)
            return null;
        return buildHelper(inorder, 0, inorder.length, postorder, 0, postorder.length);//调用方法开始重建二叉树
    }
    private TreeNode buildHelper(int[] inorder, int inorderStart, int inorderEnd, int[] postorder, int postorderStart, int postorderEnd){
        if(postorderStart == postorderEnd)//表示当前子树为空
            return null;
        int rootVal = postorder[postorderEnd - 1];//取后序遍历序列的最后一个元素作为根节点的值
        TreeNode root = new TreeNode(rootVal);//创建根节点
        int middleIndex;
        for (middleIndex = inorderStart; middleIndex < inorderEnd; middleIndex++){//用于在中序遍历中查找根节点的位置，从inorderStart开始，一直遍历到inorderEnd之前（不包括inorderEnd），直到找到根节点的值为止
            if(inorder[middleIndex] == rootVal)//如果中序遍历序列中当前索引处的值与根节点的值相等，则退出循环
                break;
        }
        //根据根节点在中序遍历中的位置，划分左右子树的边界。
        //左子树的中序遍历范围是[inorderStart, middleIndex]。
        //右子树的中序遍历范围是[middleIndex + 1, inorderEnd]。
        //左子树的后序遍历范围是[postorderStart, postorderStart + (middleIndex - inorderStart)]。
        //右子树的后序遍历范围是[leftPostorderEnd, postorderEnd - 1]。
        int leftInorderStart = inorderStart;
        int leftInorderEnd = middleIndex;
        int rightInorderStart = middleIndex + 1;
        int rightInorderEnd = inorderEnd;
        int leftPostorderStart = postorderStart;
        int leftPostorderEnd = postorderStart + (middleIndex - inorderStart);
        int rightPostorderStart = leftPostorderEnd;
        int rightPostorderEnd = postorderEnd - 1;
        root.left = buildHelper(inorder, leftInorderStart, leftInorderEnd,  postorder, leftPostorderStart, leftPostorderEnd);//递归构建左右子树
        root.right = buildHelper(inorder, rightInorderStart, rightInorderEnd, postorder, rightPostorderStart, rightPostorderEnd);
        return root;
    }
}

时间复杂度: O(n^2)

空间复杂度: O(n)

5.从前序与中序遍历序列构造二叉树

根据一棵树的前序遍历与中序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7] 返回如下的二叉树：

105. 从前序与中序遍历序列构造二叉树

思考题

前序和中序可以唯一确定一棵二叉树。

后序和中序可以唯一确定一棵二叉树。

那么前序和后序可不可以唯一确定一棵二叉树呢？

前序和后序不能唯一确定一棵二叉树！，因为没有中序遍历无法确定左右部分，也就是无法分割。

举一个例子：

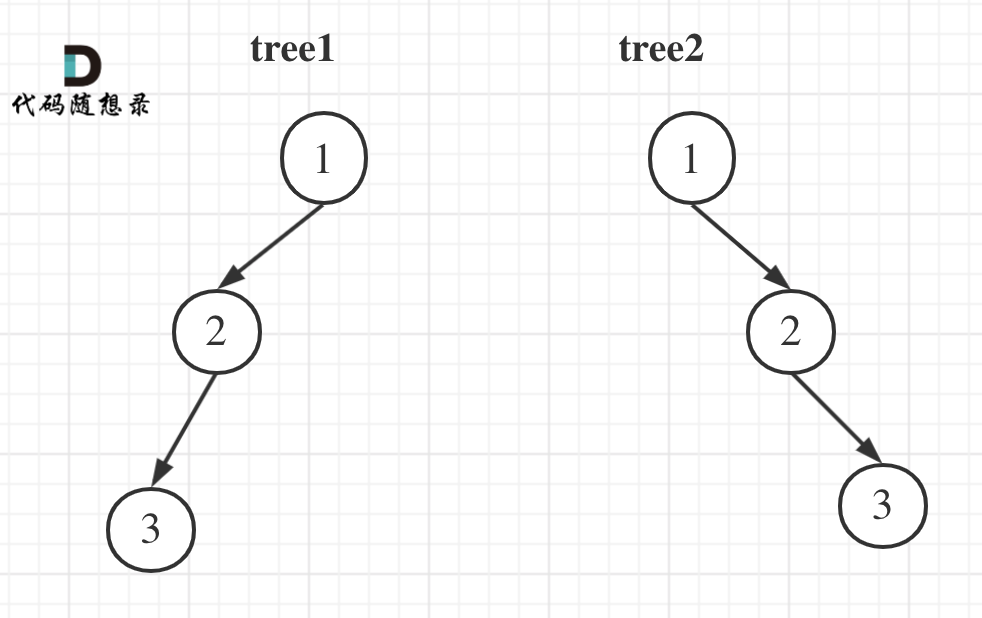
106.从中序与后序遍历序列构造二叉树2

tree1 的前序遍历是[1 2 3]，后序遍历是[3 2 1]。

tree2 的前序遍历是[1 2 3]，后序遍历是[3 2 1]。

那么tree1 和 tree2 的前序和后序完全相同，这是一棵树么，很明显是两棵树！

所以前序和后序不能唯一确定一棵二叉树！

总结

前序和中序可以唯一确定一棵二叉树，后序和中序可以唯一确定一棵二叉树，而前序和后序却不行。

public class Constructing_a_Binary_Tree_from_Preorder_and_Inorder_Traversal_Sequences {
    Map<Integer, Integer> map;//存储中序遍历序列中每个数值对应的索引位置

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        map = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) { // 用map保存中序序列的数值对应位置
            map.put(inorder[i], i);
        }

        return findNode(preorder, 0, preorder.length, inorder, 0, inorder.length);//前闭后开，调用findNode方法开始重建二叉树，传入整个前序和中序遍历序列。
    }

    public TreeNode findNode(int[] preorder, int preBegin, int preEnd, int[] inorder, int inBegin, int inEnd) {
        // 参数里的范围都是前闭后开
        if (preBegin >= preEnd || inBegin >= inEnd) {  // 不满足左闭右开，前序或中序遍历序列的索引超出范围，说明当前子树为空
            return null;
        }
        int rootIndex = map.get(preorder[preBegin]);//找到前序遍历的第一个元素在中序遍历中的位置rootIndex，这个元素是当前子树的根节点。
        TreeNode root = new TreeNode(inorder[rootIndex]);//构造根结点
        int lenOfLeft = rootIndex - inBegin;//计算左子树的大小lenOfLeft。
        //递归地调用findNode方法重建左子树和右子树，左子树的前序遍历范围是[preBegin + 1, preBegin + lenOfLeft + 1)，中序遍历范围是[inBegin, rootIndex)，右子树的前序遍历范围是[preBegin + lenOfLeft + 1, preEnd)，中序遍历范围是[rootIndex + 1, inEnd)。
        root.left = findNode(preorder, preBegin + 1, preBegin + lenOfLeft + 1,
                inorder, inBegin, rootIndex);
        root.right = findNode(preorder, preBegin + lenOfLeft + 1, preEnd,
                inorder, rootIndex + 1, inEnd);

        return root;
    }

}

时间复杂度: O(n)

空间复杂度: O(n)