POJ 1084 Square Destroyer

Square Destroyer

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 3783		Accepted: 1649

Description

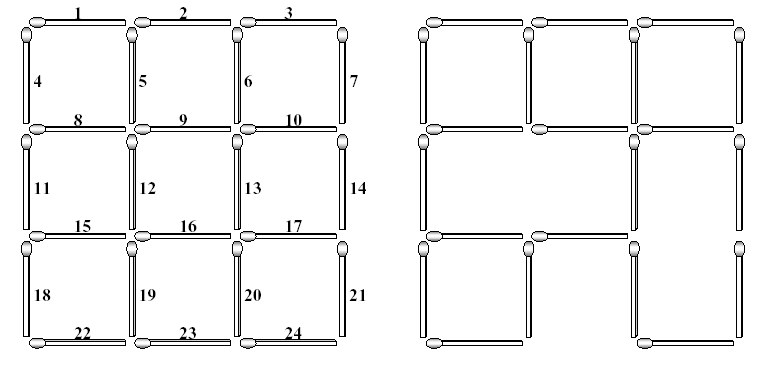
The left figure below shows a complete 3*3 grid made with 2*(3*4) (=24) matchsticks. The lengths of all matchsticks are one. You can find many squares of different sizes in the grid. The size of a square is the length of its side. In the grid shown in the left figure, there are 9 squares of size one, 4 squares of size two, and 1 square of size three.

Each matchstick of the complete grid is identified with a unique number which is assigned from left to right and from top to bottom as shown in the left figure. If you take some matchsticks out from the complete grid, then some squares in the grid will be destroyed, which results in an incomplete 3*3 grid. The right figure illustrates an incomplete 3*3 grid after removing three matchsticks numbered with 12, 17 and 23. This removal destroys 5 squares of size one, 3 squares of size two, and 1 square of size three. Consequently, the incomplete grid does not have squares of size three, but still has 4 squares of size one and 1 square of size two.

As input, you are given a (complete or incomplete) n*n grid made with no more than 2n(n+1) matchsticks for a natural number 5 <= n . Your task is to compute the minimum number of matchsticks taken
out to destroy all the squares existing in the input n*n grid.

Input

The input consists of T test cases. The number of test cases (T ) is given in the first line of the input file.
Each test case consists of two lines: The first line contains a natural number n , not greater than 5, which implies you are given a (complete or incomplete) n*n grid as input, and the second line begins with a nonnegative integer k , the number of matchsticks that are missing from the complete n*n grid, followed by
k numbers specifying the matchsticks. Note that if k is equal to zero, then the input grid is a complete n*n grid; otherwise, the input grid is an incomplete n*n grid such that the specified k matchsticks are missing from the complete n*n grid.

Output

Print exactly one line for each test case. The line should contain the minimum number of matchsticks that have to be taken out to destroy all the squares in the input grid.

Sample Input

2
2
0
3
3 12 17 23

Sample Output

3
3

Source

Taejon 2001

IDA*题，搜索每一个合法的正方形，枚举其每一条边并且删除，并且讨论每一个正方形时要从小到大讨论，这样才能保证删除的边数最少

估价函数为此时还剩的正方形的个数，注意每讨论完一个正方形要将这个正方形所有的边减去

#include<cstdio>
#include<iostream>
#include<cstring>
#define Bit(xx) ((LL)1<<(xx-1))
#define LL long long
using namespace std;
const int inf=0x7fffffff;
inline void _read(LL &x){
    char t=getchar();bool sign=true;
    while(t<'0'||t>'9')
    {if(t=='-')sign=false;t=getchar();}
    for(x=0;t>='0'&&t<='9';t=getchar())x=x*10+t-'0';
    if(!sign)x=-x;
}
LL t,n,m,all,depth,num,tot;
LL square[105],line[6][6];//line[i][j]是用二进制表示的位于i,j的正方形所有的边的集合
LL getup(LL i,LL j){return (2*n+1)*(i-1)+j;}//求位于i,j位置的正方形的上边的边的编号
LL getleft(LL i,LL j){return getup(i,j)+n;}//求位于i,j位置的正方形的左边的边的编号
void structure(){
	LL i,j,tx,ty,extend;
	for(i=1;i<=n;i++)
	    for(j=1;j<=n;j++){
	    	line[i][j]|=Bit(getup(i,j))|Bit(getup(i+1,j));
	    	line[i][j]|=Bit(getleft(i,j))|Bit(getleft(i,j+1));
	    	square[++tot]=line[i][j];
		}
	for(extend=1;extend<n;extend++)
	    for(i=1;i+extend<=n;i++)
	        for(j=1;j+extend<=n;j++){
	        	square[++tot]=0;
	        	for(tx=0;tx<=extend;tx++)
	        	    for(ty=0;ty<=extend;ty++)
	        	        square[tot]^=line[i+tx][j+ty];
			}//讨论以i,j位置的正方形为左上角的所有正方形
}
bool dfs(LL state,LL k){
	LL i,cur=0,s=state,h=0;
	for(i=1;i<=tot;i++)
	    if((s&square[i])==square[i]){
	    	h++;
	    	s^=square[i];
	    	if(!cur)cur=square[i];
		}
	if(!h)return 1;
	if(h+k>depth)return 0;
	for(i=1;i<=num;i++)
	    if(cur&Bit(i))
	        if(dfs(state^Bit(i),k+1))return 1;
	return 0;
}
void clear(){
	memset(line,0,sizeof(line));
	memset(square,0,sizeof(square));
	tot=depth=0;
}
int main(){
	_read(t);
	while(t--){
		clear();
		_read(n);_read(m);
		structure();
		num=2*n*(n+1),all=((LL)1<<num)-1;
		while(m--){
			LL x;
			_read(x);
			all^=Bit(x);
		}
		while(!dfs(all,0))depth++;
		printf("%d\n",depth);
	}
}