卡特兰数的简单介绍

最新推荐文章于 2023-12-02 14:07:49 发布

GGN_2015

最新推荐文章于 2023-12-02 14:07:49 发布

阅读量559

点赞数 2

分类专栏：算法导论 C++语言

本文链接：https://blog.csdn.net/ggn_2015/article/details/78760732

版权

算法导论同时被 2 个专栏收录

75 篇文章 0 订阅

订阅专栏

C++语言

30 篇文章 0 订阅

订阅专栏

应国老师邀请，写了一篇关于卡特兰数的博客。如有谬误，敬请同学们指出！——GGN 2017.12.9

其实我并不是很了解卡塔兰数的一些性质，我不得不承认这并不是一篇很好的博客。。

下周一月考，因为写博客耗费了大量时间，被我奶教育了。。（还有很多没写完的内容，敬请谅解）

一些约定

在下文中出现这些符号将不再定义它们的含义：

$C_n^m=\frac{n!}{(n-m)!m!}=C_{n-1}^{m-1}+C_{n-1}^{m}$ ：表示组合数，表示从n个不同的物品中选出一个元素个数为m的子集的总方案数。

$\sum_{k=1}^{n}{f(k)}=f(1)+f(2)+..+f(n)$ ：表示求和。

$H_i$ ：表示卡塔兰数的第 $i$ 项，本文中的卡塔兰数的下标统一从1开始，但我看到的大多数材料中的卡塔兰数的下标都是从0开始的（这是本文的一个不太好的地方）。

卡塔兰数

卡特兰数又称卡塔兰数，卡特兰数是组合数学中一个常出现在各种计数问题中的数列。以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)的名字来命名。——百度百科

卡塔兰数的增长较快，实验表明，用long long只能储存卡塔兰数的前36位。

一般计算方式：

H n = \sum i = 1 n - 1 H i H n - i : n > 1

$H_n=\sum_{i=1}^{n-1}H_iH_{n-i}:n>1$

H 1 = 1

$H_1=1$

低效递归实现：

int H(int n){
    int i,ans=0;
    if(n==1)return 1;
    for(i=1;i<=n-1;i++){
        ans+=H(i)*H(n-i);
    }
    return ans;
}

低效递归实现的时间复杂度巨差，我个人估计其时间复杂度为 $O(n!)$ 。

记忆化搜索实现：

#define maxn (16384+1)
long long h[maxn];
int vis[maxn];//实现记忆化，保证每个数据只计算一次

long long H(int n){
    int i;
    if(vis[n])return h[n];
    vis[n]=1;
    if(n==1)h[n]=1;
    else{
        h[n]=0;
        for(i=1;i<=n-1;i++){
            h[n]+=H(i)*H(n-i);
        }
    }
    return h[n];
}

递推实现：

#define maxn (16384+1)
long long h[maxn];

void solve(int n){
    int i,j;
    h[1]=1;
    for(j=2;j<=n;j++){//按照从小到大的顺序计算
        h[j]=0;
        for(i=1;i<=j-1;i++){
            h[j]+=h[i]*h[j-i];
        }
    }
}

这两种方法计算的时间复杂度为 $O(n^2)$ 。

另类计算方式:

组合数法：

H n + 1 = 1 n + 1 \cdot C n 2 n = C n 2 n - C n - 1 2 n

$H_{n+1}=\frac{1}{n+1}\cdot C_{2n}^{n}=C_{2n}^n-C_{2n}^{n-1}$

$O(n)$ 递推：

H n = H n - 1 \times 4 n - 6 n

$H_{n}=H_{n-1}\times \frac{4n-6}{n}$

（感谢高杨大神提供的 $O(n)$ 的先进递推方式！）

#define maxn (100+1)
long long h[maxn];
void solve(int n){
    int i,a,b;
    h[1]=1;
    for(i=2;i<=n;i++){
        h[i]=h[i-1]*(4*i-6)/i;
    }
}

卡塔兰数的数学意义

1.类比“01串”的排列

一个长度为 $2n$ 的“01串”，其中包括n个0，n个1。要求这个序列的任意长度的前缀中包含“1”的数目大于等于“0”的数目。求这样的序列的个数，其个数即为 $H_{n+1}$ 。

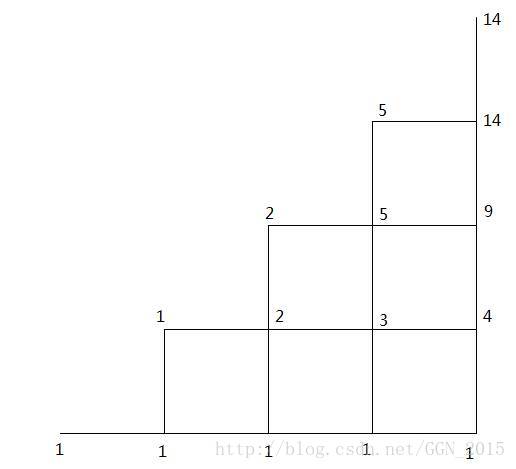
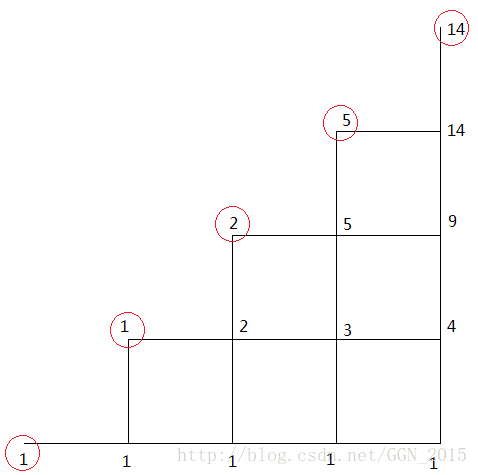
2.类比网格中的移动

方案数

在一个 $n\times n$ 的网格中，只允许向右和向上走，并且只允许走网格的下半部分（即横坐标大于等于纵坐标的部分），从左下角走到右上角的方案数。这个方案数为 $H_{n+1}$ 。

Catalan数蕴含其中

在所有 $x=y$ 的位置上发现了卡塔兰数。

推荐题目

洛谷： P1044 栈

洛谷： P1722 矩阵 II

[2017.12.27] 2017 CDQZ 联讯 Day9 学习了一种极其科学的卡塔兰数递推式的证明方法，但是因为需要插图，我有空再补上。。

[2017.12.28] 引用（著名业余）数学家费马的一句话

“我已经发现了一种极其巧妙的证明方法证明它（“它”指费马大定理），可惜这里空白地方太小（还有就是我太懒了），不下。”　——皮耶·德·费马

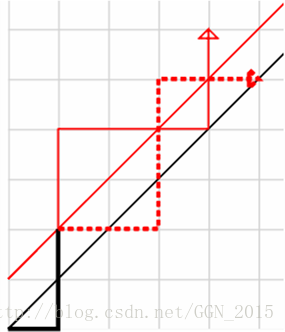
卡塔兰数证明

↑ 这张图片揭示了卡塔兰数线性递推证明的全部奥秘，待脑洞大开的同学们去探索、追寻。。

p.s. : 大约1637年左右，法国学者费马在阅读丢番图（Diophatus）《算术》拉丁文译本时，曾在第11卷第8命题旁写道：“将一个立方数分成两个立方数之和，或一个四次幂分成两个四次幂之和，或者一般地将一个高于二次的幂分成两个同次幂之和，这是不可能的。关于此，我确信已发现了一种美妙的证法，可惜这里空白的地方太小，写不下。”

（拉丁文原文: “Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.”）